Примеры использования интегрального исчисления в задачах экономического характера
Определенный интеграл применяют для вычисления суммарных экономических эффектов, общих, маргинальных взносов и т.д. Рассмотренные примеры не исчерпывают всех возможных применений определенного интеграла в экономике.
Затраты, доход и прибыль
Пусть 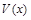 будет функцией общих затрат на производство х единиц продукции,
будет функцией общих затрат на производство х единиц продукции, 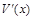 – функция маргинальных затрат. Тогда определенный интеграл
– функция маргинальных затрат. Тогда определенный интеграл
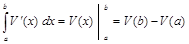 (1)
(1)
равняется изменению общих затрат при росте количества произведенной продукции от а до b единиц.
Отсюда вытекает важное следствие:
Изменение производственных затрат при росте произведенной продукции от а до b единиц равняется площади криволинейной трапеции, ограниченной графиком функции маргинальных затрат 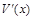 , отрезком
, отрезком 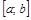 и прямыми
и прямыми 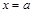 и
и 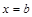 .
.
Аналогично, если 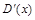 и
и 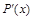 – функции маргинального дохода и прибыли при росте реализации произведенной продукции от а до b единиц вычисляется по формулам:
– функции маргинального дохода и прибыли при росте реализации произведенной продукции от а до b единиц вычисляется по формулам:
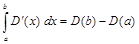 ; (2)
; (2)
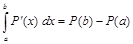 . (3)
. (3)
Пример 1. Функция маргинальных затрат фирмы имеет вид 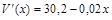 .
.
Найти рост общих затрат, когда производство возрастет с 1000 до 2000 единиц.
Решение. По формуле
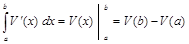
рост общих затрат будет:
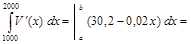
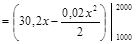
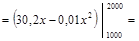
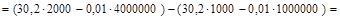
= 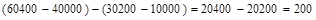 .
.
Итак, затраты возрастут на 200 гривен.
Максимизация прибыли во времени
Пусть 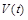 ,
, 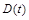 и
и 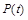 – общие затраты, доход и прибыль, которые изменяются за время t. Тогда
– общие затраты, доход и прибыль, которые изменяются за время t. Тогда
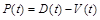 , или
, или 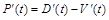 .
.
Максимум общей прибыли будет тогда, когда
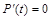 , или
, или 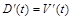 .
.
Другими словами, существует такое время 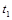 , когда
, когда 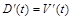 , т.е. скорости изменения дохода и затрат равны.
, т.е. скорости изменения дохода и затрат равны.
Общая прибыль за время 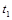 можно найти по формуле
можно найти по формуле
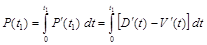 .
.
Пример 2. Скорости изменения затрат и дохода предприятия после начала его деятельности определялись формулами
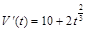 и
и 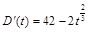 ,
,
где 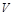 и
и 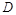 измерялись миллионами гривен, а t – годами. Определить, как долго предприятие было прибыльным, и найти общую прибыль, которая было получено за это время.
измерялись миллионами гривен, а t – годами. Определить, как долго предприятие было прибыльным, и найти общую прибыль, которая было получено за это время.
Решение. Оптимальное для предприятия время 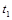 получим из условия
получим из условия 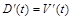 :
:
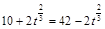 ;
;
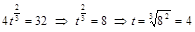 .
.
Итак, предприятие было прибыльным 4 года, за это время было получена прибыль
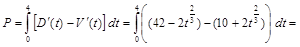
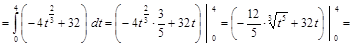
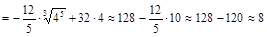 (млн. гр.).
(млн. гр.).
Дисконтная прибыль
Пусть функция 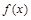 описывает изменение производительности работы некоторого предприятия за определенное время. Найдем объем продукции
описывает изменение производительности работы некоторого предприятия за определенное время. Найдем объем продукции 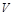 , которая выпущена за промежуток времени
, которая выпущена за промежуток времени 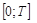 .
.
Известно, что если производительность работы за некоторое время постоянная, то объем продукции за промежуток времени 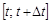 задается формулой
задается формулой 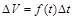 . В общем случае справедлива формула
. В общем случае справедлива формула 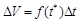 , где
, где 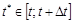 , которая тем точнее, чем меньше
, которая тем точнее, чем меньше 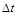 .
.
Разобьем отрезок 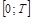 на п частей, т.е.:
на п частей, т.е.: 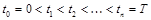 .
.
Для величины объема продукции 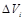 , который выпущен за время
, который выпущен за время 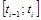 , имеем:
, имеем: 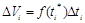 ;
; 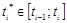 . Тогда
. Тогда
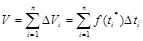 .
.
Если 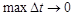 , то
, то
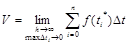
Поэтому по определению интеграла
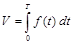 ,
,
если 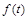 – производительность работы в момент времени t, тогда
– производительность работы в момент времени t, тогда 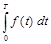 – объем продукции, которая выпущена за промежуток времени от 0 до T.
– объем продукции, которая выпущена за промежуток времени от 0 до T.
Определение начальной суммы по ее конечной величине, полученной за t лет при годовом проценте Р, называется дисконтированием.
Задачи этого класса встречаются при определении экономической эффективности капитальных вложений.
Пусть 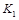 – конечная сумма, которая получена за t лет, которую в финансовом анализе называют современной суммой. Если проценты простые, то
– конечная сумма, которая получена за t лет, которую в финансовом анализе называют современной суммой. Если проценты простые, то 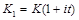 , где
, где 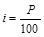 – процентная ставка.
– процентная ставка.
Тогда 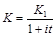 .
.
Если проценты сложные, то 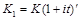 , поэтому
, поэтому 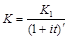 .
.
Пусть прибыль за год изменяется во времени и описывается функцией 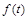 при удельной норме процента, равной i, процент начисляется непрерывно.
при удельной норме процента, равной i, процент начисляется непрерывно.
Дисконтная прибыль К за время Т вычисляется по формуле:
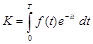 , где
, где 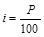 .
.
Пример 3. Определить дисконтную прибыль за 3 года при процентной ставке 8%, если базовые капиталовложения составили 10 млн. гривен, а ожидаемый прирост капитала 1 млн. гривен.
Решение.Очевидно, что капиталовложения задаются функцией
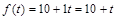 .
.
Получим дисконтную сумму капиталовложений по формуле:
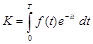 , где
, где 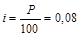 .
.
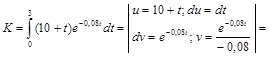
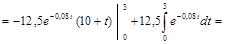
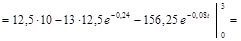
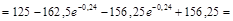
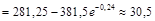 млн. гривен.
млн. гривен.
Это означает, что получение одинаково нарощенной суммы через три года ежегодные вклады от 10 до 13 млн. гривен равновесны одновременному начальному вкладу 30,5 млн. гривен при той же непрерывной процентной ставке.
Пусть известна функция 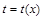 , которая задает изменение затрат t на изготовление продукции в зависимости от степени освоения производства, где х порядковый номер изделия в партии товара.
, которая задает изменение затрат t на изготовление продукции в зависимости от степени освоения производства, где х порядковый номер изделия в партии товара.
Тогда среднее время 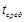 , затраченное на изготовление одного изделия в период освоения от а до b изделий, вычисляется по теореме о среднем значении определенного интеграл:
, затраченное на изготовление одного изделия в период освоения от а до b изделий, вычисляется по теореме о среднем значении определенного интеграл:
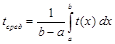 .
.
Что касается функции изменения затрат времени 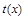 , то как правило, она такова:
, то как правило, она такова: 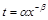 , где
, где 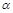 – затрата времени на одно изделие;
– затрата времени на одно изделие; 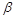 – показатель производственного процесса.
– показатель производственного процесса.
Пример 4. Найти среднее время, которое затрачено на освоение выпуска одного изделия в период освоения от 10 до 20 изделий, если затрата времени на 1-но изделие 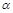 = 200 мин., показатель производственного процесса
= 200 мин., показатель производственного процесса 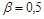 .
.
Решение. По формуле
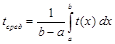
имеем:
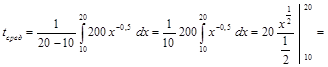
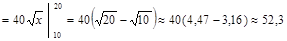 мин.
мин.
