II. Изучение нового материала. Работа с текстом по плану:
Работа с текстом по плану:
1. При помощи какого инструмента выполняют вычисления?
2. Какие арифметические действия можно выполнять с помощью микрокалькулятора?
3. С чего начинается работа на микрокалькуляторе?
4. Как ввести в микрокалькулятор натуральное число? Десятичную дробь?
5. Как сбросить число с индикатора?
6. Выполните действия на микрокалькуляторе.
Вывешивается плакат.
| СЛОЖЕНИЕ | |
| Задание | 2,5 + 0,6 = |
| Последовательность операций | 2,5  0,6 0,6  3,1 3,1 |
| ВЫЧИТАНИЕ | |
| Задание | 2,5 – 0,6 = |
| Последовательность операций | 2,5  0,6 0,6  1,9 1,9 |
| УМНОЖЕНИЕ | |
| Задание | 10,5 × 3 = 31,5 |
| Последовательность операций | 10,5  3 3  31,5 31,5 |
| ДЕЛЕНИЕ | |
| Задание | 10,5 : 3 = 3,5 |
| Последовательность операций | 10,5  3 3  3,5 3,5 |
7. Почему прибор называется «микрокалькулятор»?
От греческого слова «mikros» – малый, от латинского слова «calculation» – счет, вычисления.
III. Закрепление.
1. № 1536, 1537, 1539 (а, б), 1538 (а–г) (1-е пары чисел), 1540 (а, д).
2. На повторение № 1548 (а), 1555 (а, б), 1549.
IV. Итог урока.
1. Обратить внимание на правильное написание слов: микрокалькулятор, табло, индикатор, клавиатура, клавиши.
2. Ответить на вопросы п. 39.
3. Вычислить с помощью калькулятора: 871,017 : 5,05 – 11,376.
V. Домашнее задание: п. 39; № 1556 (а–г), 1557 (а), 1559, 1547. Прочитать с. 317 (об истории развития вычислительных устройств). В математический словарь: микрокалькулятор.
Урок № 141
Микрокалькулятор (п. 39)
Оборудование: листочки для записи ответов к устным заданиям.
Ход урока
I. Проверка домашнего задания.
1. Сообщение консультантов о результате выполнения домашнего задания.
2. Проверить правильность решения № 1557 (а), 1559, 1545.
II. Устные упражнения.
1. Составить задачу по числовому выражению:
(3,8 + 3,7 + 3,6) : 3.
а) Как по-другому можно назвать это выражение?
б) Что называется средним арифметическим?
2. Задания по вариантам: устно вычислить и записать только ответ.
| Вариант I | Вариант II |
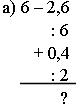 | 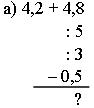 |
| б) Выполнить деление: | |
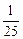 ; 1 : 2: 0,8 : 0,04. ; 1 : 2: 0,8 : 0,04. | 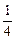 ; 5 : 0,2; 1 : 1,25 ; 5 : 0,2; 1 : 1,25 |
| в) Каким одним действием можно уменьшить число в 10 раз? | в) Каким одним действием можно уменьшить число в 100 раз? |
| г) Каким одним действием можно увеличить число в 1000 раз? | Каким одним действием можно увеличить число в 100 раз? |
Листы сдаются на проверку.
III. Работа по теме урока.
1. № 1539 (в, г), 1538 (а–г) (2-е и 3-и пары чисел), 1540 (б, г).
2. На повторение № 1546 (б), 1551, 1555 (в), 1553.
IV. Итог урока.
1. Вопросы к п. 39.
Самостоятельная работа
| Вариант I | Вариант II |
| а) Вычислите с помощью микрокалькулятора: | |
| 43,5 × (387,38 + 392,43) – 920,035 94,27 × 3,796 : 4,7135 – 5,38 (438,25322 : 53,78 + 24,051) × 4,2867 3,22226 : 4,39 × 0,245 – 0,04483 | (4,3257 + 2,8345) × 53,9 – 5,00478 5,843 × 74,86 : 2,9215 + 30,28 (377,26366 : 431,8 + 0,7463) × 39,831 72,4176 : 85,6 × 4,35 – 0,0584 |
V. Домашнее задание: п. 39; № 1556 (д, е), 1557 (б), 1560, 1558.
Урок № 142
Проценты (п. 40, ч. 1)
Цели:научить давать определение процента, обозначать, читать и находить процент чисел и величин, переводить процент в десятичную дробь и обратно.
Оборудование: плакаты для устных упражнений и объяснения нового материала.
Ход урока
I. Устные упражнения.
1. Квадрат ABCD разделен на равные части. Площадь заштрихованной фигуры равна 6 м2. Найдите площадь квадрата AВCD.
(Вывешивается плакат.)
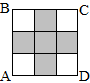
2. Учитель: Если вы правильно выполните вычисления и выпишите в таблицу буквы, соответствующие найденным ответам, то узнаете тему сегодняшнего урока.
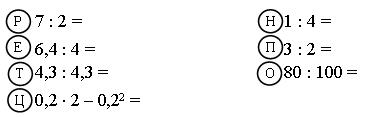
Примечание: сначала вычисляются примеры, а потом открывается таблица.
| 3,5 | 0,8 | 0,36 | 1,6 | 0,25 | 0,1 | |
Итак, тема нашего урока «Проценты».
