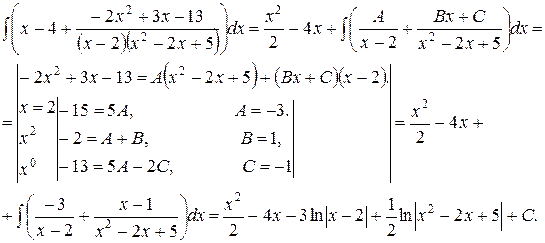Лекция 37. Основные методы интегрирования. Интегрирование рациональных дробей, интегралы от иррациональных функций

Всякую рациональную функцию можно представить в виде рациональной дроби, т.е. в виде отношения двух многочленов:

.

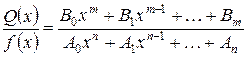Не ограничивая общность рассуждений, будем предполагать, что эти многочлены не имеют общих корней.

Если степень числителя ниже степени знаменателя, то дробь называется правильной, в противном случае дробь называется неправильной.

Если дробь неправильная, то, разделив числитель на знаменатель ( по правилу деления многочленов), можно представить дробь в виде суммы многочлена и некоторой правильной дроби:

,

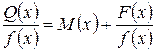где М(х) – многочлен, а 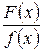- правильная дробь.

Пример 1. Пусть дана неправильная рациональная дробь 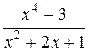. Разделив числитель на знаменатель ( по правилам деления многочленов ), получаем: .

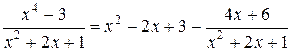Естественно интегрирование многочленов не вызывает никаких проблем. Нам осталось научиться интегрировать правильные рациональные дроби. Оказывается, что всякую рациональную дробь можно представить в виде суммы простейших дробей. Сам факт разложения любой рациональной дроби в сумму простейших дробей мы обсудим чуть позже. А пока выясним какие же дроби относятся к простейшим и как их интегрировать.

Определение. Правильные рациональные дроби вида:

1) ,

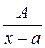2) 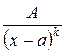(k – целое положительное число ),

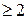3) 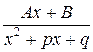( корни знаменателя комплексные, т.е. ),

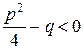4) 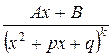(k – целое положительное число 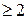, корни знаменателя комплексные )

называются простейшими дробями 1,2,3 и 4 типов.

Интегрирование первых трех типов не представляет особых трудностей. Рассмотрим их интегрирование в общем виде.

1). .

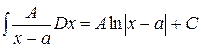2). .

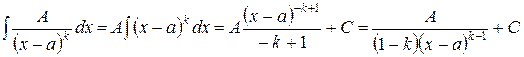3).

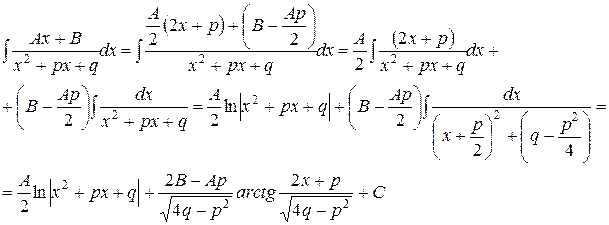
Интегрирование простейшей дроби четвертого типа более трудоемко и рассматривать мы его не будем. Желающие ознакомиться с этим алгоритмом могут использовать любой учебник по высшей математике, например учебник Пискунова Н.С. «Дифференциальное и интегральное исчисление» т.1.

Теперь вернемся к проблеме разложения рациональной дроби на простейшие. Пусть нам дана правильная рациональная дробь 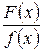. Будем предполагать, что коэффициенты входящих в нее многочленов – действительные числа и что данная дробь несократима ( последнее означает, что числитель и знаменатель не имеют общих корней ). Справедливы следующие теоремы, которые мы представим без доказательства ( доказательство см. Пискунов Н.С. «Дифференциальное и интегральное исчисление» т.1 ):

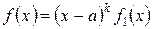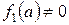Теорема 1. Пусть х=а есть корень знаменателя кратности k, т.е. , где , тогда данную правильную дробь 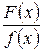можно представить в виде суммы двух других правильных дробей следующим образом:

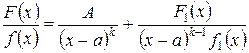, (1)

где А – постоянная, не равная нулю, а 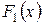- многочлен, степень которого ниже степени знаменателя .

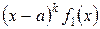Следствие.К правильной рациональной дроби 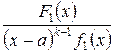, входящей в равенство (1), можно применить аналогичное рассуждение. Таким образом, если знаменатель имеет корень x=a кратности k, то можно написать:

,

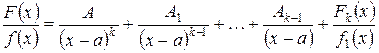где 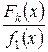- правильная несократимая дробь. К ней также можно применить только что доказанную теорему, если 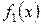имеет другие действительные корни. Вторая теорема рассматривает случай комплексных корней знаменателя.

Теорема 2. Если 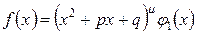, где многочлен 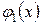- не делться на 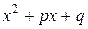, то правильную рациональную дробь 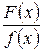можно представить в виде суммы двух других правильных дробей следующим образом:

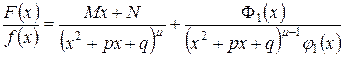, (2)

где Ф₁(х) – многочлен, степень которого ниже степени многочлена .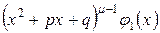

Применяя теперь к правильной дроби 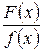результаты теорем 1 и 2, мы можем выделить последовательно все простейшие дроби, соответствующие всем корням знаменателя f(x). Рассмотрим основные случаи.

Случай 1. Корни знаменателя действительны и различны, т.е. f(x)=(x-a)(x-b)…(x-d). В этом случае дробь 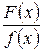разлагается на простейшие дроби 1-го типа:

,

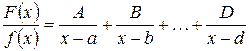и тогда

.

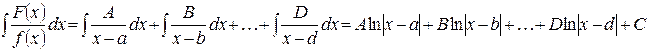Случай 2. Корни знаменателя действительные, причем некоторые из них кратные: .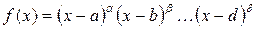

В этом случае дробь 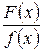разлагается на простейшие дроби 1и 2 типов.

Случай 3. Среди корней знаменателя есть комплексные неповторяющиеся (т.е. различные):

.

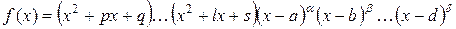В этом случае дробь 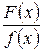разлагается на простейшие дроби 1, 2 и 3 типов.

Случай 4. Среди корней знаменателя есть комплексные кратные:

.

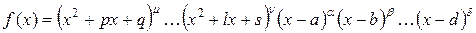В этом случае разложение дробь 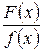будет содержать и простейшие дроби 4-го типа.

Из всего изложенного следует, что интеграл от любой рациональной функции может быть выражен через элементарные функции в конечном виде, а именно:

1) через логарифмы – в случае простейших дробей 1 типа;

2) через рациональные функции – в случае простейших дробей 2 типа;

3) через логарифмы и арктангенсы – в случае простейших дробей 3 типа;

4) через рациональные функции и арктангенсы – в случае простейших дробей 4 типа.

Осталось выяснить как на практике разложить правильную рациональную дробь на сумму простейших. Пусть у нас есть дробь со знаменателем

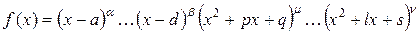, то дробь 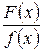может быть представлена в виде

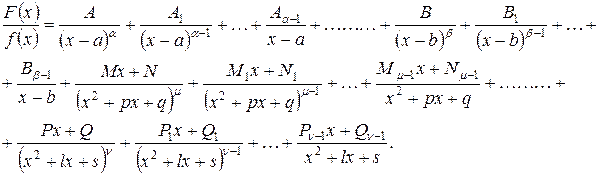(3)

Написанное равенство есть тождество, поэтому приведя дроби к общему знаменателю, получим тождественные многочлены в числителях справа и слева. Приравнивая коэффициенты при одинаковых степенях х, получим систему уравнений для определения неизвестных коэффициентов А, А₁, …, В, В₁, … . Этот метод нахождения коэффициентов называется методом неопределенных коэффициентов.

В дополнение к этому методу, в целях упрощения получаемой системы можно пользоваться методом частных значений. Проще говоря, поскольку многочлены, получившиеся в правой и левой частях равенства, после приведения к общему знаменателю должны быть тождественно равны, то их значения равны при любых частных значениях х. Придавая х «удачные» значения ( например, значения действительных корней знаменателя ) мы получим уравнения для определенных коэффициентов.

Пример 2. Пусть требуется разложить дробь 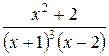на простейшие. На основании теорем 1 и 2 и общей формулы (3) имеем:

.

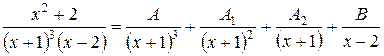Приведем к общему знаменателю и приравняем числители, получим:

,

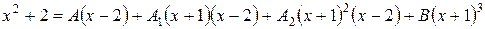или

.

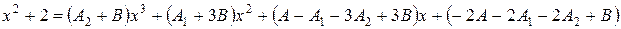Найдем коэффициенты А,А₁,А₂,В.

1 способ: приравнивая коэффициенты при х³,х², х¹,х⁰ (свободный член), т.е. используя метод неопределенных коэффициентов, получим систему уравнений для определения коэффициентов:

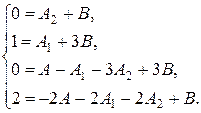(4)

Решая эту систему, найдем А=-1, А₁=1/3, А₂=-2/9, В=2/9.

2 способ: прежде чем решать не такую уж и простую систему, имеет смысл её немного упростить, найдя часть коэффициентов с помощью метода частных значений. Пусть

x=-1, получим 3=-3А или А=-1;

х=2, получим 6=27В; В=2/9.

Подставим их значения в систему (4), тем самым сократив количество неизвестных в ней до двух, что гораздо проще.

В результате мы получаем разложение:

.

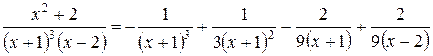В заключение лекции найдем некоторые неопределенные интгералы.

Пример 3. Найти неопределенный интеграл .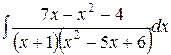

Решение. Подынтегральная функция представляет собой рациональную правильную дробь, т.к. степень числителя 2, а степень знаменателя 3. Таким образом выделять целую часть не нужно. Разложим её знаменатель на множители: 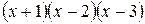. Согласно случаю 1, в разложении правильной дроби на простейшие каждому множителю знаменателя вида (х-а) соответствует слагаемое 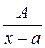. Поэтому в данном случае имеем :

.

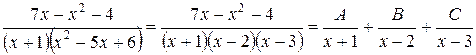Приведя правую часть последнего равенства к общему знаменателю и приравняв числители дробей, получим тождество

.

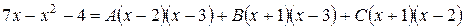Коэффициенты А,В,С определим с помощью метода частных значений.

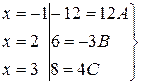, откуда А=-1,В=-2,С=2. Подставив найденные коэффициенты в разложение подынтегральной функции на простейшие дроби, получим

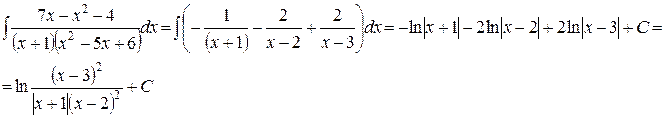
Пример 4. Найти неопределенный интеграл .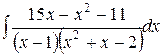

Решение. Этапы нахождения интеграла полностью аналогичны примеру 3. Единственная разница в том, что при нахождении коэффициентов мы будет использовать оба описанных метода, комбинируя их.

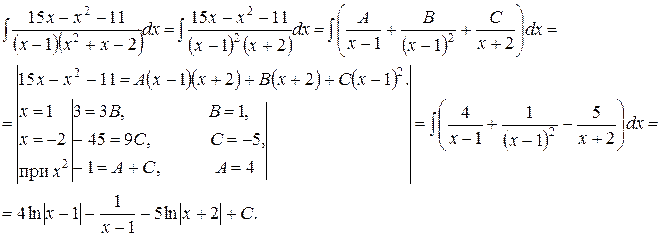
Пример 5. Найти неопределенный интеграл .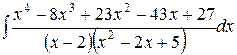

Решение. Так как подынтегральная функция является неправильной дробью, то путем деления числителя на знаменатель можно представить её в виде суммы целого многочлена и правильной рациональной дроби: