Тема 10. Выборка и ее представление. Выборочные моменты

Математическая статистика – это раздел математики, изучающий математические методы обработки статистических данных с целью построения вероятностной модели случайного явления.

Исходными данными в математической статистике являются результаты статистического эксперимента, представленные в численном виде.

Статистический эксперимент обычно состоит из 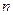отдельных наблюдений за некоторой случайной величиной . Результат отдельного наблюдения случаен и может быть описан случайной величиной .

Совокупность результатов всех наблюдений называется выборкой. Конкретные значения, полученные в эксперименте, называются выборочными значениями . Число элементов выборки 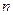называется объемом выборки.

На основе выборочных значений строятся оценки функции распределения и числовых характеристик генеральной совокупности.

Пусть из генеральной совокупности извлечена выборка, причем значение наблюдалось 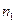раз, значение наблюдалось 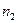раз, …, наблюдалось раз. Объем выборки Выборочные значения 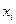иначе называются вариантами, а последовательность вариант, записанная в возрастающем порядке – вариационным рядом. Число 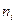называют частотойварианты 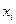, а число называют относительной частотой. Разность называется размахом выборки.

Важной характеристикой вариационного ряда является его медиана (или середина), которая равна при нечетном 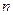, т.е. и при четном объеме выборки .

Выборочным распределением (статистическим рядом) называют перечень вариант и соответствующих им частот или относительных частот.

Пример 1. Задано распределение частот выборки объема . Написать распределение относительных частот.

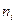Решение: , ,

, .

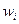	0,15	0,5	0,35

Для наглядности статистический ряд представляют графически в виде полигонов и гистограмм частот.

Полигон, как правило, служит для изображения дискретного статистического ряда и представляет собой ломаную линию, в которой концы отрезков прямой имеют координаты , ,..., . Полигоном относительных частот называют ломаную, отрезки которой соединяют точки , ,..., .

Гистограмма (статистический аналог плотности) служит для изображения интервальных (непрерывных) статистических рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака и высотами, равными частотам. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения. Для построения гистограммы используют метод группировки: т.е. область возможных значений разбивают на некоторое число непересекающихся интервалов , подсчитывают количество наблюдений, попавших в соответствующий интервал – это 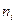, , и строят кусочно-постоянную функцию , где – длина соответствующего интервала. Заметим, что метод группировки применяется и для дискретных данных. Относительные частоты n_i/n в любом случае являются статистическими аналогами (оценками) для вероятностей.