Характеристическое уравнение

Пусть х – собственный вектор квадратной матрицы А порядка п. Тогда имеет место матричное уравнение

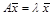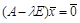, или , (4)

где 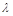– собственное значение матрицы А, а Е и 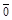– соответственно, единичная матрица и нулевой вектор-столбец. Поскольку собственный вектор не является нулевым, то однородная система (4) должна иметь ненулевое решение, т. е. в силу следствия 2 (см. ранее) определитель этой системы равен нулю:

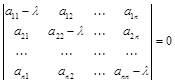. (5)

Определитель системы однородных уравнений (4) называется характеристическим многочленом, а уравнение (5) –характеристическим уравнением матрицы А.

Уравнение (5) имеет степень п относительно неизвестной 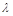. Его корни являются собственными числами матрицы А. Определив набор этих чисел, для каждого из них можно найти соответствующий собственный вектор как решение однородной системы (4).

Пример 2. Найти собственные числа и собственные векторы матрицы .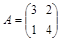

Решение. Характеристическое уравнение для этой матрицы имеет вид 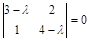, откуда, раскрывая определитель, получаем:

.

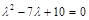Корни этого уравнения 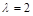, 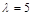. Для нахождения собственных векторов подставим найденные собственные значения в систему однородных уравнений (4) при 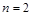, соответствующей заданной матрице А. Собственный вектор, соответствующий собственному значению 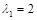, является решением системы

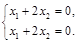
По сути дела, это одно уравнение, поскольку определитель системы равен нулю. Полагая 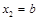свободной переменной, получаем первый собственный вектор 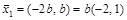. Подстановка второго собственного значения 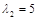приводит к системе уравнений

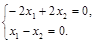
которая через свободную переменную 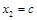определяет второй собственный вектор матрицы А: .

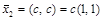Поскольку 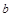и с – произвольные числа, то одному собственному значению может соответствовать несколько собственных векторов разной длины. Например, собственные векторы, соответствующие фундаментальным решениям однородных систем (в данном случае их будет по одному на каждое собственное значение), имеют вид, .

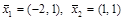Пример 3. Найти общее решение, частное решение и фундаментальную систему решений для СЛАУ:

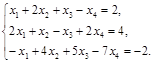
Решение: Матрицы А и С имеют вид

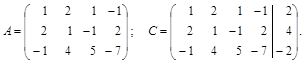
Их ранги 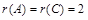, значит, СЛАУ совместна.

Выделим следующую подсистему

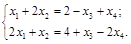
Считая 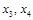известными, ее решение найдем по формулам Крамера:

,

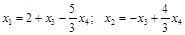где 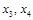могут принимать произвольные значения.

Общее решение системы имеет вид

.

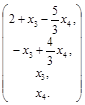Частное решение системы получим, например, при , :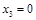

.

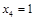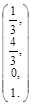Давая свободным неизвестным поочередно значения, равные элементам столбцов определителя, порядка количества свободных неизвестных, в данном случае второго

,

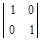получим векторы

,

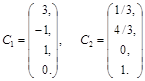представляющие собой фундаментальную систему решений.

Общее решение теперь можно записать следующим образом:

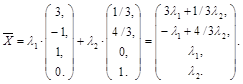
Придавая коэффициентам 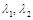различные числовые значения, получим различные частные решения. Любое частное решение можно получить путем подходящего выбора коэффициентов .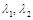