Упражнения к разделу 2.2

1. Найти уравнение геометрического места точек, равноудален-ных от точек 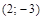и .

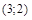Ответ: .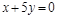

2 Найти уравнение геометрического места точек, расстояние каждой из которых от прямой 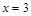равно расстоянию от точки .

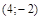Ответ: .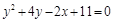

3. Найти уравнение окружности, центр которой находится в точке 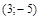и радиус которой равен 4.

Ответ: .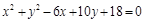

4.Найти уравнение окружности, диаметром которой является отрезок прямой 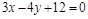, содержащийся между осями координат.

Ответ: .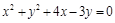

5.Найти центр и радиус окружности .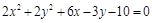

Ответ: .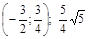

6.Найти длины осей, эксцентриситет и координаты фокусов эллипса .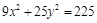

Ответ: .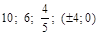

7. Найти уравнение эллипса, фокусы которого имеют координаты 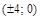, а длина большой оси равна 10.

Ответ: .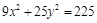

8. Найти уравнение эллипса, у которого длина малой оси равна 6 и один из фокусов имеет координаты .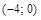

Ответ: .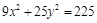

9. Найти уравнение эллипса, если известно, что он проходит через точк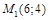и и .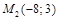

Ответ: .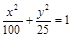

10. Найти эксцентриситет, координаты фокусов и уравнения асимптот гиперболы .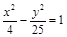

Ответ: .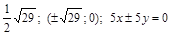

11. Найти уравнение гиперболы, у которой фокусы имеют координаты 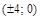и действительная ось равна 6.

Ответ: .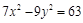

12. Найти уравнение равносторонней гиперболы, проходящей через точку .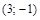

Ответ: .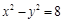

13. Найти координаты вершины и фокуса и уравнения оси директрисы параболы .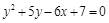

Ответ: .

14. Найти уравнение параболы, вершина которой находится точке 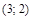и фокус в точке .

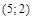Ответ: .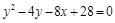

15. Привести уравнение кривой второго порядка к каноническому виду и построить:

1) .

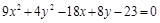2) .

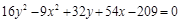3) .

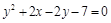4) .

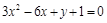Ответ:

1) 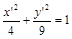; эллипс с центром в точке .

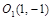2) 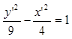; ; 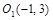гипербола, пересекающая ось .

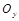3) 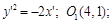парабола с осью, параллельной оси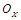

4) .

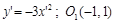16. Найти точки равновесия и области дохода и затрат компании, изготовляющей ежемесячно х изделий стоимостью р гривен, а сумма общих ежемесячных затрат 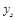имеет такую закономерность:

1) ;

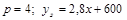2) ;

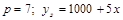3) ;

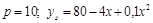4) .

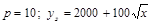Ответ:1) 500; 2) 500; 3) 40 или 20; 4) 400.

Задания для индивидуальной семестровой работы студентов к главе 2

1.Даны три силы 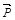, , 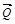, 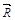приложенные к одной точке. Вычислить работу равнодействующей силы, когда ее точка приложения перемещается из точки В в точку .

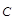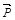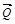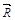№				В	С
	2,-1, 3	1, 2, 0	-1, 0, 0	1, 1, 1	2, 1, 1
	1, 2, 0	-1, 0,-1	2, 1, 2	1, 2, 3	1, 1, 1
	-1, 1, 1	2, 1, 1	1, 2, 2	1, 0, 0	2, 1,-1
	1, 0, 1	1,-2, 2	-1, 2, 1	2,-1, 0	2, 0, 1
	-1, 2, 1	0, 0, 1	0, 1, 1	3,-1, 2	1, 2, 1
	0, 1, 1	1, 2,-2	2, 1, 3	4, 2,-1	2, 1, 1
	1,-1, 1	0,-1, 1	1, 2, 1	3, 1, 2	2, 1, 0
	2, 1, 3	1, 2,-1	0,-1, 2	1,-1, 0	0, 1, 2
	2,-1, 3	2, 1,-3	-1, 2, 1	2, 0, 1	4, 2, 1
	1,-1, 3	-2, 0,-1	1, 2, 0	0, 2, 1	3, 1, 1
	1, 0, 2	-2, 0, 1	2, 1, 1	0, 0, 1	1,-1, 0
	1, 1, 0	2, 0, 0	1,-1, 2	1,-1, 1	2, 1, 1
	-1, 0, 2	2, 1,-1	1,-1, 1	2, 1, 0	1,-1, 1
	1, 1, 1	3, 2,-2	-2, 1, 0	3, 1,-2	1,-1, 2
	2,-1, 0	1,-2, 1	-1, 0, 2	2,-1, 0	2, 1, 1
	1,-1, 2	2, 1,-1	-2, 1, 1	2, 2, 1	1, 1, 1
	2, 0, 2	1,-1, 2	0,-1,-2	3, 1,-1	2, 1, 4
	2, 1, 0	1, 3,-1	-2, 1, 3	2,-1, 1	2, 1, 2
	1, 2, 3	2, 1, 1	-1, 2,-2	4, 1,-1	3, 1, 1
	1, 0,-2	1, 2, 0	1,-2, 1	3, 2, 2	2, 2, 3
	2,-1, 1	1,-1, 1	-1, 0, 0	3,-1, 1	2, 3, 1
	1, 2,-1	2,-1, 3	1,-2, 0	2,-2, 1	1, 1,-1
	3, 1, 2	1, 2,-1	2,-1, 0	1, 1, 2	2, 1, 1
	2, 1,-3	1, 2, 2	-2,-1, 3	1, 0, 2	1, 2, 1
	-2, 0, 1	1, 2, 0	-1, 2, 0	-1, 0, 1	2,-1, 1
	1, 0,-1	2,-1, 3	3, 2,-2	3, 0,-2	1, 2, 3
	0, 2, 3	3, 1, 2	0, 2, 0	2,-1, 3	3, 1, 0
	1, 2, 3	-1, 1, 1	2,-1, 3	3,-2, 1	4, 0, 2
	3, 2, 1	1,-1, 2	-1, 2, 1	2, 0,-1	3, 2,-1
	2,-1, 2	0, 2, 3	2, 0,-1	1,-2, 1	2, 2, 1

2.Вычислить площадь параллелограмма, построенного на векторах 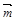и 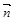, если известны:

№

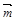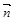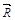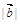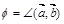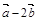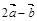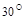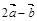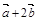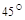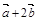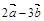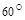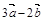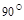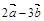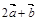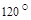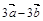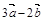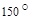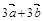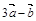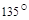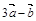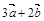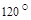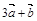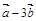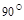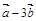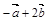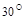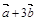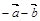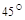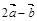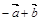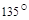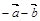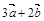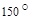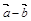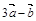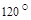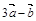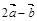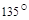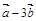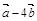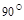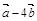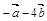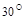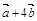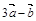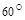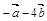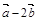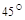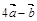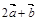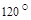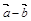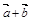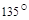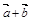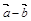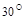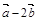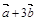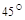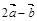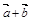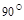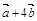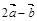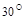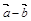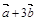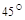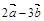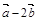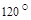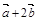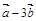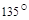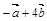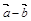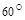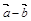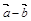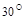3.Даны вершины треугольника АВС. Найти:

1) длину стороны ВС;

2) уравнение ВС;

3) уравнение высоты АМ;

4) длину высоты АМ;

5) площадь треугольника АВС;

6) величину угла В;