Экзаменационные билеты (І семестр)

1. МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ. ОСНОВНЫЕ ЧИСЛОВЫЕ МНОЖЕСТВА. ВЫСКАЗЫВАНИЯ. ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД ВЫСКАЗЫВАНИЯМИ.

Множества и операции над ними.

Множество – совокупность(группа, набор, и т.д) объектов обладающих одинаковыми свойствами.

Множества можно задавать:

1) Буквами: А, В, С

2) Перечислением элементов: {1, 3, 5}

3) Геометрически (круги Эйлера-Вена)

Круги Эйлера- Венна геометрическое изображение множество.

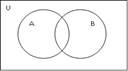
1) а ϵ А (элемента принадлежит А)

2) а ϵ А (элемент а не принадлежит множество А)

3) А ʗ В (множество А включено в В)

4) А = В (множества А и В равны)

5) А = ᴓ (А – пустое множество)

6) А{аǀР(а)} – множество А состоит из элементов обладающих свойствам Р (а) А А={а₁, а₂, а₃}

Основные операции над множествами

1) Объединение множеств: А˅В

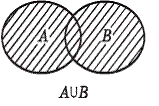А = {С, А} В= {Ш, А} А˅В= {С,А,Ш,А}

2) Пересечение множеств: А˄В

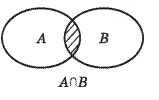А = {С, А} В= {Ш, А} А˄В= {А}

3) Разность множеств: А\В

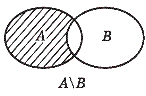
4) Дополнение множеств:

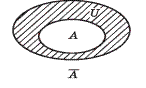
Количество элементов множества записывается в виде: m(A)

Если m(A) – количество элементов множества А, а m(В) – множества В то справедливо равенство: m(A˅В)= m(A)+ m(B)-m(A˄B)

Основные числовые множества.

Z – множество целых чисел

N – множество натуральных чисел

R – множество действительных чисел

Q – множество иррациональных чисед

C – множество комплексных чисел

Высказывания.

Простое высказывание – утверждение, в отношении которого можно сказать, истинно оно или ложно. Значения высказывания обозначают: 1-истина; 0-ложь.

Сложное высказывание- получают из простых при помощи логических операций, к которым относятся отрицание, конъюнкция, дизъюнкция, импликация, эквивалетность (эквиваленция).

Логические операции над высказываниями.

1) ОТРИЦАНИЕ: Ā (читается не А)

А	Ā

2) КОНЬЮНКЦИЯ: А˄В (А и В) (как умножение)

А	В	А˄В

3) ДИЗЬЮНКЦИЯ: А˅В (А или В) (как сложение)

А	В	А˅В

4) ИМПЛИКАЦИЯ: А=> В (если А, то В)

А	В	А=>В

5) ЭКВИВАЛЕНЦИЯ А<=> В (А тогда и только тогда когда В)

А	В	А<=>В

1. ФАКТОРИАЛ. МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИЯ. БИНОМ НЬЮТОНА. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ: (A±B) ³, A±B³

Факториал.

Факториал числа — это произведение натуральных чисел от 1 до самого числа. n! = 1*2*3*….:n!

N! = (n-1) * n

Пример: 3! = 1 · 2 · 3 = 6; 6! = 1 · 2 · 3 · 4 · 5 · 6 = 720

Метод математической индукция.

ММИ – метод доказательства истинности некоторого утверждения зависящего от n где ϵ N.

Схема доказательства

1) Непосредственная проверка при n=1

2) Допускаем при n=R

3) Доказываем истинность при n=R+1

Бином Ньютона.

(a+в)ⁿ = aⁿ + na^n-1 в + С²_n a^n-2 в² +…..+С^n-1_n ав^n-1 +вⁿ

C²_n, C³_n –биномиальные коэффициенты

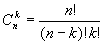
Треугольник Паскаля находит при разложении на множители произвольной степени двучлена (a + b):

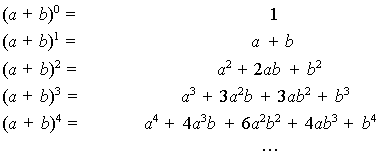
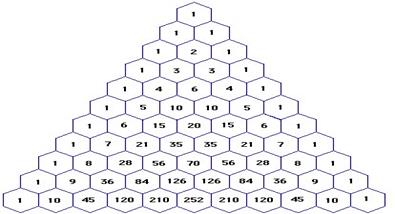
Формулы сокращенного умножения: (a±b) ³, a³±b³

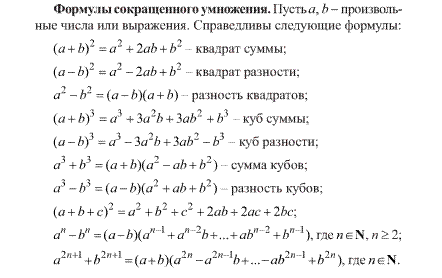
3. ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА, И АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ.

Комлексным числом z называется число вида. Выражение вида z=x+iy, где х и у- действительные число, а i- так называемая мнимая единица, i² = -1 назыв. компексным числам.

Если числе z=x+iy х=0, то z=0+iy –К.Ч называется чистомнимым. У=0, то z=x+i*0= х – действительное число(таким образом любое число – К.Ч)

В К.Ч z=x+iy число х- называется действительной частью и обозначается х= Re(Z), число у – называется мнимой частью и обозначается у= Jm(Z)

i – мнимая единица (i² =-1)

Два К.Ч. равны тогда и только тогда когда равны их действительные и мнимые части

Замечание: К.Ч. Z=0 тогда и только тогда когда x=y=0. Понятия «больше» или «меньше» для К.Ч. нет!

Два комплексных числа z=x+iy и 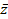=x+iy, которые отличаются только знаком мнимой части называются сопряженными.

Противоположным числу z=x+iy есть число - z=x+iy

Обратным числу z=x+iy есть число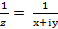

Комлексным числом z называется число вида. Выражение вида z=x+iy, где х и у- действительные число, а i- так называемая мнимая единица, i² = -1 назыв. компексным числам.

Для комплексных чисел, записанных в алгебраической форме, определены операции сумма, разность, произведение, частное.

1) Сумма: Z₁ = x₁ + i*y₁ и Z₂ = x₂ + i*y₂

есть К.Ч.: Z₁ + Z₂ = (x₁ + x₂) + (y₁ + y₂) *i

2) Разность: Z₁ = x₁ + i*y₁ и Z₂ = x₂ + i*y₂

есть К.Ч.: Z₁ - Z₂ = (x₁ - x₂) + (y₁ - y₂) *i

3) Произведение: Z₁ = x₁ + i*y₁ и Z₂ = x₂ + i*y₂

есть К.Ч.: Z₁ * Z₂ = (x₁ + i*y₁) * (x₂ + i*y₂) = x₁ * x₂ + i*x₁y₂ + i*x₂y₁ + i² y₁y₂ = (x₁x₂ – y₁y₂) + (x₁y₂ + x₁y₂) *i

4) Частное: Z₁ = x₁ + i*y₁ и Z₂ = x₂ + i*y₂

есть К.Ч.: = = = =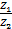

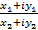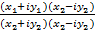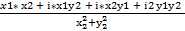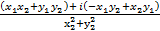
5) возведение в степень:

i²=-1;

i³ = i² * i=-1 *i=-i

i⁴ =i³*i=-i=-i*i=-i²=-(-1)=1

i⁵ = i⁴ * i=1 *i=i

i⁶ =i⁵*i=i*i=i²=-1

i⁷ = i⁶ * i=-1 *i=-i

I4*R=1 I4*R+1=i I4*R+2=-1 I4*R+3=-i

4. ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА, ДЕЙСТВИЯ НАД ЧИСЛАМИ В ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ. ПОКАЗАТЕЛЬНАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА.

Тригонометрическая форма комплексного числа.

Всякое комплексное число z=x+iy можно изобразить в виде точки М(х,у) но плоскости ХОУ, где х=Re(Z), у=Jm(Z)

у

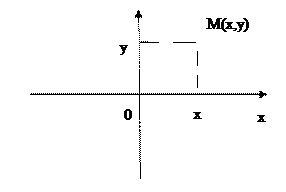
Плоскость на которой изображены комплексные числа называется комплексной плоскостью.

Ось ОХ (абсцисс) – называется действительной

Ось ОУ (ардиной) – мнимой осью

Комплексное число z=x+iy также можно задавать в виде радиус-вектора 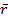= = 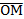(х,у)

Длина вектора 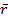, называется модулем числа Z и обозначается 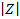или r. 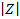= r можно вычислить по формуле: 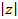= r = 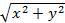, где х=Re(Z) y=Jm(Z)

Величина угла, между положительным направлением оси ОХ и радиус – вектором 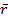называется аргументом числа Z и обозначается (фи) или arg Z

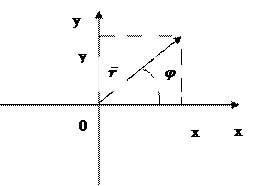Аргумент можно вычислить по формуле:

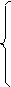arctg , если Z в 1 или четверти

= argZ = arctg + П, если 2 четверти

arctg - П, если 3 четверти

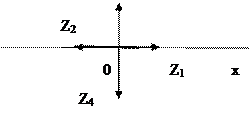
Частный случаи: если К.Ч. попала на одну из осей ОХ или ОУ, а не между ними, то

Arg Z₁ =0

Arg Z₂ =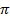

Arg Z₃ =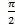

Arg Z₄ = -

y

Z3

Если К.Ч. z=x+iy записано в виде: z = r(cos + i sin ), то говорят, что оно записано в тригонометрической форме, где r = 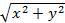, = arg

Действия над числами в тригонометрической форме.

Пусть Z₁ = r₁(cos ₁ + i*sin ₁)
Z₂ = r₁(cos ₂ + i*sin ₂)

1) Произведение:

Z₁ * Z₂= r₁ * r₂(cos( ₁+ ₂) +i*sin( ₁ + ₂))

2) Частное

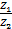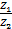= (cos( ₁ – ₂₎ +i*sin( ₁ - ₂))

3) Возведение в степень (Формула Муавра)

Zⁿ = rⁿ(cos(n * ₎ + sin(n * )

4) Извлечение корня n-й степени:

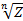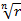= (cos 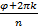+ i*sin 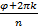), k = 0,1,….;(n-1)

Показательная форма комплексного числа.

Используя формулу Эйлера:

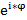= cos + i*sin

Любое комплексное число

;

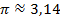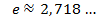Z = r(cos + i*sin ) можно записать как: Z = r * 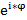такая запись называется показательная форма К.Ч.