Примерный перечень вопросов к экзамену 2-го семестра
1. Матрицы, классификация матриц. Операции над матрицами, их свойства.
2. Определитель. Свойства определителя. Правила вычисления определителя 2-го и 3-го порядков.
3. Минор, алгебраическое дополнение элемента. Вычисление определителя n-го порядка. Разложение определителя по элементам строки (столбца).
4. Системы линейных уравнений. Методы решения: матричный метод, метод Гаусса, формулы Крамера.
5. Декартовы и полярные координаты на плоскости. Связь между ними.
6. Прямая на плоскости. Уравнение прямой при различных параметрах ее задания.
7. Взаимное расположение прямых. Угол между прямыми.
8. Линии 2-го порядка. Каноническое уравнение эллипса, его основные характеристики.
9. Каноническое уравнение гиперболы, её основные характеристики.
10. Каноническое уравнение параболы, её основные характеристики.
11. Вектор на плоскости и в пространстве. Способы задания. классификация векторов. Координаты вектора. Линейные операции над векторами в координатной форме.
12. Произведение векторов: скалярное произведение, векторное произведение, смешанное произведение. Свойства произведений.
13. Предел функции в точке. Основные теоремы о пределах.
14. Непрерывность функции в точке и на интервале. Точки разрыва. Односторонние пределы.
15. Раскрытие неопределенностей вида 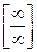 ,
, 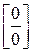 .
.
16. Первый и второй замечательные пределы.
17. Правило Лопиталя.
18. Понятие функции нескольких переменных. Примеры. Предел функции двух переменных. Геометрический смысл частных производных.
19. Частные производные и частные дифференциалы функции двух переменных.
20. Дифференцируемость сложной функции нескольких переменных.
21. Частные производные высших порядков. Теорема Шварца.
22. Экстремумы функций двух переменных. Необходимое условие экстремума. Достаточное условие экстремума функции двух переменных.
23. Дифференциальные уравнения. Определение, классификация ДУ. Решение дифференциального уравнения. Задача Коши.
24. Дифференциальные уравнения 1-го порядка с разделяющимися переменными.
25. Линейные однородные дифференциальные уравнения 1-го порядка.
26. Простейшие дифференциальные уравнения n-го порядка. Понижение порядка в дифференциальных уравнениях.
27. Однородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Характеристическое уравнение.
28. Случайное событие, классификация.
29. Классическое определение вероятности случайного события. Свойства вероятности.
30. Элементы комбинаторики: перестановки, размещения, сочетания без повторений Алгебра событий. Теоремы сложения и умножения вероятностей.
31. Условное событие. Формула полной вероятности. Формула Байеса.
32. Повторение испытаний. Формула Бернулли. Наивероятнейшее число появлений события.
33. Локальная и интегральная теоремы Лапласа.
34. Дискретная случайная величина. Ее числовые характеристики.
35. Способы задания дискретной случайной величины.
36. Непрерывная случайная величина. Ее числовые характеристики.
37. Интегральная функция распределения вероятностей случайной величины.
38. Дифференциальная функция распределения вероятностей непрерывной случайной величины.
39. Нормальный закон распределения случайной величины. Правило «трех сигм».
40. Равномерное распределение. Числовые характеристики.
41. Генеральная совокупность. Выборка. Вариационные ряды. Графическое представление данных.
42. Статистические оценки параметров распределения. Требования к оценкам.
43. Средние величины. Определения, формулы
44. Показатели вариации распределения.
45. Ошибки измерений. Интервальная оценка генеральных параметров
46. Доверительная вероятность. Уровень значимости.
47. Статистические гипотезы. Ошибки 1-го и 2-го рода.
48. Статистические критерии. Мощность критерия.
49. Одновыборочный и двухвыборочный t-критерий Стьюдента.
- F-критерий Фишера. Критерий согласия хи-квадрат.
- Элементы дисперсионного анализа. Однофакторный дисперсионный анализ.
- Исследование зависимостей. Линейный регрессионный анализ.
- Уравнения регрессии. Коэффициент регрессии.
- Корреляция. Коэффициент корреляции.
