Формы и методы контроля и оценки результатов обучения
7.1 Текущий контроль по учебным занятиям
7.2 Тестовый контроль на входе
7.3 Выполнение и оценка ИПЗ.20
8Критерии оценок
8.1При контроле и оценки усвоения базовых знаний учитывается:
- точность воспроизведения основных понятий, определений, характеристик дифференциальных уравнений
8.2 При контроле и оценки освоения базовых умений учитывается:
- правильность поиска и алгоритма решения дифференциального уравнения;
- отсутствие ошибок при выполнении алгебраических преобразований и интегрировании;
- точность выполнения алгоритма решения, получение верных ответов
8.3 Оценка выполнения ИПЗ.20:
- «Отлично» - выполнен полный объем заданий в соответствии с п.8.2 или в одном из заданий допущена ошибка при выполнении алгебраических преобразований;
- «Хорошо» - выполнен полный объем заданий в соответствии с п.8.2, но допущены ошибка при выполнении алгебраических преобразований в 2-х заданиях;
- «Удовлетворительно» - в соответствии с п.8.2 выполнены 3 задания;
- «Неудовлетворительно» - в соответствии с п.8.2 выполнено менее 3-х заданий, студентом не реализованы цели работы
Приложение А
Контрольные вопросы по учебному элементу УЭ.08.01
Дифференциальные уравнения первого порядка
1 Что называется дифференциальным уравнением первого порядка?
2 Какие дифференциальные уравнения называются обыкновенными?
3 Как записывается дифференциальное уравнение в явном виде?
4 Как записывается дифференциальное уравнение в неявном виде?
5 Как записывается дифференциальное уравнение в дифференциальной форме?
6 Что называется решением дифференциального уравнения?
7 Какие типы решений дифференциального уравнения различают?
8 Сколько решение имеет дифференциальное уравнение? (ответ обосновать)
9 Что называется общим интегралом дифференциального уравнения и как записывается общий интеграл?
10 Как называется геометрическая интерпретация общего решения дифференциального уравнения?
11 Что необходимо задать, чтобы найти частное решение дифференциального уравнения?
12 Как задаются начальные условия дифференциального уравнения первого порядка и как записываются?
13 Что геометрически означает задание начальных условий дифференциального уравнения первого порядка?
14 Как называется геометрическая интерпретация частного решения дифференциального уравнения?
15 Теорема Коши о существовании и единственности решение дифференциального уравнения первого порядка
16 Определение дифференциального уравнения с разделяющимися переменными. Алгоритм решения
17 Определение однородного дифференциального уравнения первого порядка.
Алгоритм решения
18 Определение линейного дифференциального уравнения первого порядка.
Алгоритм решения
Приложение Б
Содержание индивидуального практического задания
Задание 1Найдите общие интегралы (общие решения) дифференциальных уравнений первого порядка с разделяющимися переменными
| 1.1 | 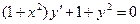 | 1.13 | 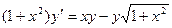 |
| 1.2 | 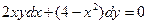 | 1.14 | 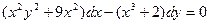 |
| 1.3 | 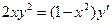 | 1.15 | 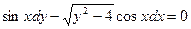 |
| 1.4 | 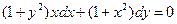 | 1.16 | 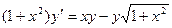 |
| 1.5 | 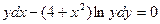 | 1.17 | 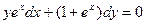 |
| 1.6 | 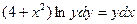 | 1.18 | 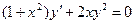 |
| 1.7 | 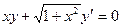 | 1.19 | 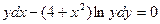 |
| 1.8 | 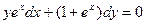 | 1.20 | 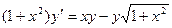 |
| 1.9 | 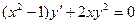 | 1.21 | 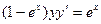 |
| 1.10 | 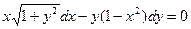 | 1.22 | 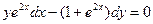 |
| 1.11 | 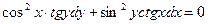 | 1.23 | 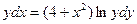 |
| 1.12 | 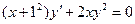 | 1.24 | 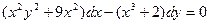 |
Задание 2Найдите общие интегралы (общие решения) однородных дифференциальных уравнений первого порядка
| 2.1 | 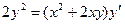 | 2.13 | 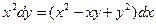 |
| 2.2 | 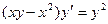 | 2.14 | 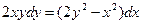 |
| 2.3 | 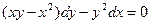 | 2.15 | 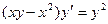 |
| 2.4 | 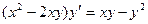 | 2.16 | 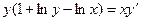 |
| 2.5 | 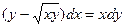 | 2.17 | 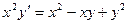 |
| 2.6 | 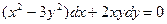 | 2.18 | 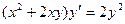 |
| 2.7 | 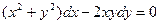 | 2.19 | |
| 2.8 | 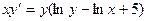 | 2.20 | 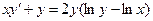 |
| 2.9 | 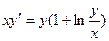 | 2.21 | |
| 2.10 | 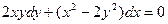 | 2.22 | 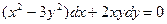 |
| 2.11 | 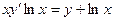 | 2.23 | 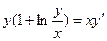 |
| 2.12 | 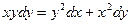 | 2.24 | 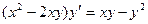 |
Приложение Б
(продолжение)
Задание 3Найдите общие интегралы (общие решения) линейных дифференциальных уравнений первого порядка
| 3.1 | 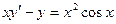 | 3.13 | 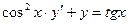 |
| 3.2 | 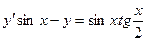 | 3.14 | 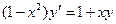 |
| 3.3 | 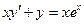 | 3.15 | 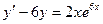 |
| 3.4 | 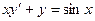 | 3.16 | 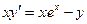 |
| 3.5 | 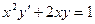 | 3.17 | 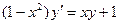 |
| 3.6 | 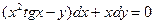 | 3.18 | 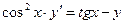 |
| 3.7 | 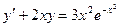 | 3.19 | 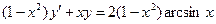 |
| 3.8 | 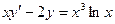 | 3.20 | 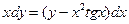 |
| 3.9 | 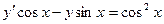 | 3.21 | 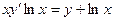 |
| 3.10 | 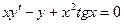 | 3.22 | 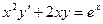 |
| 3.11 | 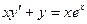 | 3.23 | 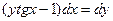 |
| 3.12 | 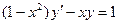 | 3.24 | 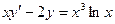 |
Задание 4Найдите частные решения дифференциальных уравнений первого порядка
| 4.1 | 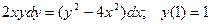 | 4.13 | 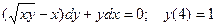 |
| 4.2 | 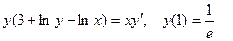 | 4.14 | 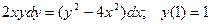 |
| 4.3 | 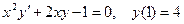 | 4.15 | 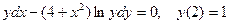 |
| 4.4 | 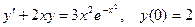 | 4.16 | 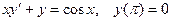 |
| 4.5 | 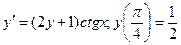 | 4.17 | 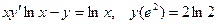 |
| 4.6 | 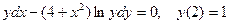 | 4.18 | 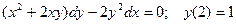 |
| 4.7 | 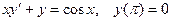 | 4.19 | 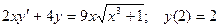 |
| 4.8 | 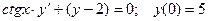 | 4.20 | 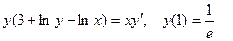 |
| 4.9 | 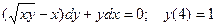 | 4.21 | 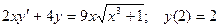 |
| 4.10 | 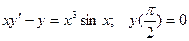 | 4.22 | 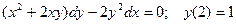 |
| 4.11 | 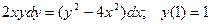 | 4.23 | 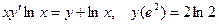 |
| 4.12 | 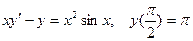 | 4.24 | 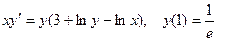 |
Приложение Б
(окончание)
Задание 5Найдите общие интегралы (общие решения) дифференциальных уравнений первого порядка
| 5.1 | 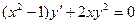 | 5.13 | 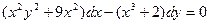 |
| 5.2 | 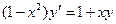 | 5.14 | 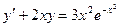 |
| 5.3 | 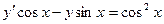 | 5.15 | 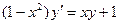 |
| 5.4 | 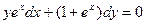 | 5.16 | 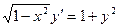 |
| 5.5 | 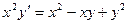 | 5.17 | 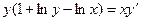 |
| 5.6 | 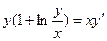 | 5.18 | 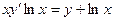 |
| 5.7 | 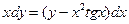 | 5.19 | 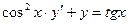 |
| 5.8 | 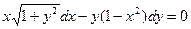 | 5.20 | 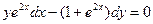 |
| 5.9 | 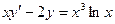 | 5.21 | 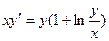 |
| 5.10 | 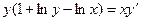 | 5.22 | 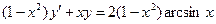 |
| 5.11 | 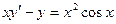 | 5.23 | 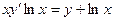 |
| 5.12 | 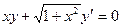 | 5.24 | 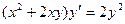 |
Задание 6Найдите общие интегралы (общие решения) дифференциальных уравнений первого порядка
| 6.1 | 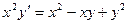 | 6.13 | 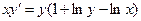 |
| 6.2 | 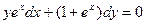 | 6.14 | 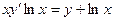 |
| 6.3 | 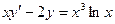 | 6.15 | 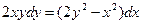 |
| 6.4 | 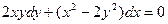 | 6.16 | 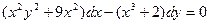 |
| 6.5 | 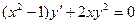 | 6.17 | 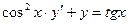 |
| 6.6 | 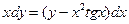 | 6.18 | 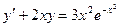 |
| 6.7 | 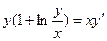 | 6.19 | 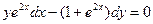 |
| 6.8 | 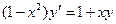 | 6.20 | 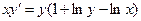 |
| 6.9 | 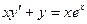 | 6.21 | 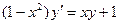 |
| 6.10 | 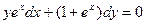 | 6.22 | 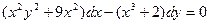 |
| 6.11 | 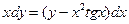 | 6.23 | 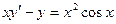 |
| 6.12 | 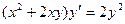 | 6.24 | 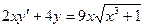 |
