Указания по выполнению контрольных работ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной 4-5 см для замечаний рецензента.
2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия, имя и отчество студента, его учебный номер (шифр), название дисциплины, номер контрольной работы. Здесь же следует указать название учебного заведения и дату отсылки работы в академию.
3. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не зачитываются.
4. Решения задач надо располагать в порядке возрастания их номеров, сохраняя номера задач.
5. Перед решением каждой задачи надо полностью выписать её условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.
6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения.
7. После получения прорецензированной работы, как не зачтённой, так и зачтённой, студент должен исправить все отмеченные рецензентом ошибки и недочёты и выполнить все рекомендации рецензента. Если рецензент предлагает ввести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.
Вместе с исправленными заданиями должна обязательно находиться прорецензированная работа и рецензия на неё. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после её рецензирования запрещается.
8. Номера задач, которые студент должен включить в свою контрольную работу, определяются по таблице вариантов. Номер варианта совпадает с последней цифрой учебного номера (шифра) студента.
Таблица вариантов
| Вариант | Номера задач контрольных заданий в1семестре |
| Контрольная работа № 1 | |
| 1.1 2.1 3.1 | |
| 1.2 2.2 3.2 | |
| 1.3 2.3 3.3 | |
| 1.4 2.4 3.4 | |
| 1.5 2.5 3.5 | |
| 1.6 2.6 3.6 | |
| 1.7 2.7 3.7 | |
| 1.8 2.8 3.8 | |
| 1.9 2.9 3.9 | |
| 1.10 2.10 3.10 |
| Вариант | Номера задач контрольных заданий во 2 семестре | |
| Контрольная работа № 2 | Контрольная работа № 3 | |
| 4.1 5.1 6.1 | 7.1 8.1 9.1 | |
| 4.2 5.2 6.2 | 7.2 8.2 9.2 | |
| 4.3 5.3 6.3 | 7.3 8.3 9.3 | |
| 4.4 5.4 6.4 | 7.4 8.4 9.4 | |
| 4.5 5.5 6.5 | 7.5 8.5 9.5 | |
| 4.6 5.6 6.6 | 7.6 8.6 9.6 | |
| 4.7 5.7 6.7 | 7.7 8.7 9.7 | |
| 4.8 5.8 6.8 | 7.8 8.8 9.8 | |
| 4.9 5.9 6.9 | 7.9 8.9 9.9 | |
| 4.10 5.10 6.10 | 7.10 8.10 9.10 |
Рекомендуемая литература:
Основная литература:
1. Шипачев В.С. Высшая математика. – М.: Высшая школа, 2007 г.
2. Шипачев В.С. Задачник по высшей математике. – М.: Высшая школа 1998 г. и любое последующее издание.
Дополнительная литература:
3. Письменный Д.Т. Конспект лекций по высшей математике: полный курс – М.: Айрис-пресс, 2007 г.
Рабочая учебная программа курса
И методические указания к изучению предмета
Курс математики разбит на темы. По каждой теме указана литература, рекомендуемая для изучения и задачи для самостоятельного решения. Номера в скобках ( ) означают номер пособия из приведенного выше списка литературы. В каждой теме приведены методические рекомендации и вопросы для самопроверки. Темы объединены в разделы. После изучения раздела нужно выполнить очередную контрольную работу.
РАЗДЕЛ 1.
Введение в математический анализ.
Дифференциальное исчисление функции одной переменной
ТЕМА 1. Введение в математический анализ. ([1], гл.2, гл. 4); ([2] стр.47 № 238, 240, 258, 235).
Функция. Обзор элементарных функций.
Числовая последовательность, её предел. Бесконечно малые и бесконечно большие величины.
Теоремы о пределах. Замечательные пределы. Сравнение бесконечно малых.
Непрерывность функций. Точки разрыва. Непрерывность основных элементарных функций. Свойства функций, непрерывных на отрезке.
Методические указания
Понятие предела одно из наиболее важных и трудных в математическом анализе. Определение предела функции в точке и в бесконечности сопровождайте рисунком. Типы точек разрыва также иллюстрируйте графически. Чтобы освоить технику вычисления пределов, разберите примеры, решённые в задачниках (2), (3). Обратите внимание, какие пределы вычисляются на основе двух «замечательных» пределов.
Вопросы для самопроверки
1. Определение предела последовательности.
2. Определение предела функции при х→ а и при х→∞.
3. Понятие бесконечно малой и бесконечно большой. Примеры.
4. Основные теоремы о пределах.
5. Первый и второй замечательные пределы.
6. Определение непрерывности функции в точке и на отрезке. Точки разрыва. Непрерывность элементарных функций.
ТЕМА 2. Дифференциальное исчисление функции одной переменной. ([1], гл.5, гл.6); ([2] стр.55 № 11, 13, 21, 31, 35, 49, 53, 63, 81) .
Определение производной функции, её геометрический смысл. Непрерывность функции, имеющей производную. Производная суммы, произведения и частного функций.
Производная сложной и обратной функции. Таблица производных.
Дифференциал функции, его геометрический смысл.
Правило Лопиталя для различных видов неопределённостей.
Исследование функций: условия возрастания и убывания функций, экстремум, выпуклость и вогнутость, точки перегиба, асимптоты.
Методические указания
Выучите наизусть таблицу производных основных элементарных функций. Умение находить производные сложных функций необходимо для успешной сдачи экзамена и дальнейшего изучения высшей математики.
При изучении темы «экстремум функции» довольно распространённой ошибкой является использование необходимого условия экстремума вместо достаточного. На самом деле обращение в некоторой точке производной в нуль не является достаточным условием наличия в этой точке экстремума. Например, производная функции у=x 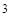 равна нулю в точке х=0, но в этой точке функция не имеет экстремума.
равна нулю в точке х=0, но в этой точке функция не имеет экстремума.
Вопросы для самопроверки
1. Определение производной. Её геометрический смысл, её механический смысл.
2. Производная суммы, произведения, частного.
3. Производная сложной функции.
4. Таблица производных основных элементарных функций.
5. Определения возрастающей и убывающей на отрезке функции. Достаточные признаки возрастания и убывания.
6. Определения точки максимума и точки минимума функции. Экстремум. Необходимое условие экстремума. Достаточные условия экстремума.
