Результат на консольном окне
Федеральное агентство по образованию
ГОУ ВПО «УГТУ – УПИ имени первого Президента России Б.Ельцина»
Кафедра «Автоматизированные электрические системы»
Курсовая работа
«Оценка точности методов численного интегрирования»
Преподаватель Котов О.М.
Руководитель Котов О.М.
Студент
Екатеринбург 2009
Изложение Варианта Задания
Оценка точности численного интегрирования функции Sinxс нижним пределом –π/2 и верхним 0, кратность равна 400 c помощью метода Симпсона
Постановка Задачи в Математическом
Для функции f(x)= Sinx на интервале [–π/2,0] рассчитать определённый интеграл приближенным и точным методами, оценить погрешность и вывести результаты на консоль.
Для приближенного вычисления определенного интеграла использовать метод Симпсона с кратностями: 0,25m,0,5m,0,75m,m,1,25m,1,5m при m=400 и с дополнительным членом равным 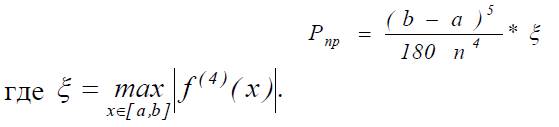
Исходный Код Программы
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace ConsoleApplication2
{
using System;
class Интеграл1
{
struct Integral
{
float a, b;
int m;
public Integral(float ina, float inb, int inm)
{
a = ina < inb ? ina : inb;
b = ina < inb ? inb : ina;
m = inm;
}
public override string ToString()
{
string s;
float Delta = (float)(ИнтСимпсона - Лейбниц) / Лейбниц * 100;
Delta = Math.Abs(Delta);
s = String.Format("\n {0}\t\t {1:f3}\t\t {2:f3}\t\t {3} %", m, h, ИнтСимпсона, Delta);
return s;
}
public float Fx(float x)
{ return (float)Math.Cos(x) * (-1); }
public float fx(float x)
{ return (float)Math.Sin(x); }
public float Лейбниц
{
get
{ return Fx(b) - Fx(a); }
}
public float h
{
get
{ return (b - a) / m; }
}
public double ИнтСимпсона
{
get
{
float k = 0, s = 0, sum, x;
for (int i = 0; i < m; i++)
{
x = a + i * h;
if ((i + 1) % 2 == 0)
k += fx(x);
else
{
s += fx(x);
}
}
float f; f = fx(a);
float g; g = fx(b);
float p=((b-a)*(b-a)*(b-a)*(b-a)*(b-a))/180*16*m*m*m*m;
sum = (float)((h / 3) * (f + g + 4 * k + 2 * s));
return sum;
}
}
}
static void Main(string[] args)
{
Console.Title = "Интегрирование функции f(x) = Sinx";
Console.WriteLine("Функция\tПределы интегрирования\t Точное значение\t Метод расчета");
Console.WriteLine("\n Sinx\t a=-П/2 b=0\t -1.000\t Выходящие прямоугольники");
Console.WriteLine("\n-----------------------------------------------------------------------------");
Console.WriteLine("\n m\t\t h\t Интеграл(приближенно)\tОтносительная ошибка");
for (int m = 100; m <= 600; m += 100)
{
Integral obj = new Integral(((float)Math.PI / 2) * (-1), 0, m);
Console.WriteLine(obj.ToString());
}
Console.ReadLine();
}
}
}
Блок – Схема
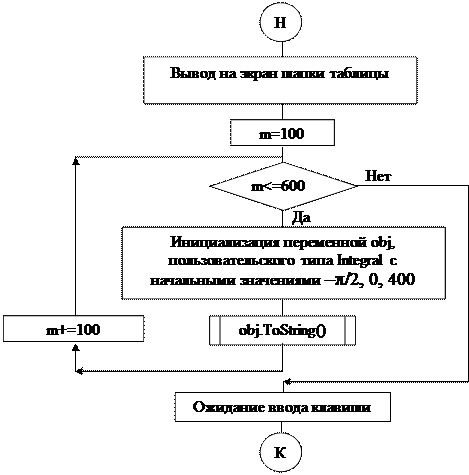 | |||
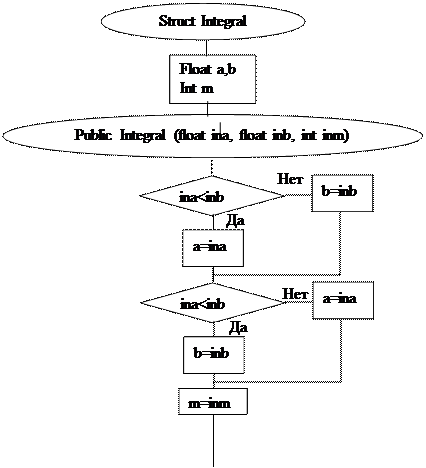 |
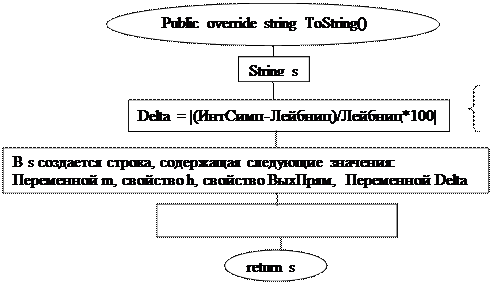 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
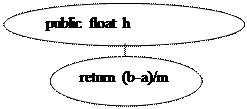 |
Схема Типа Integral
 |
Результат на консольном окне
Выводы:
В ходе выполненной курсовой работы была разработана программа для вычисления значения определенного интеграла для функции Sin(x)на отрезке от [;0] методом выходящих прямоугольников с кратностью интегрирования400.
Также было вычислено точное значение интеграла по аналитической формуле.
Была определена зависимость относительной ошибки метода от кратности интегрирования: с увеличением последней, первая убывала и затем колебалась в пределах значения 0,1%. Наиболее точное значение интеграла было найдено при кратности интегрирования равной 600.
