Плоскость в пространстве
Общим уравнением плоскости в пространстве называется уравнение
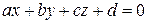 .
.
Вектор 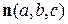 называется нормальным вектором плоскости. Если даны две плоскости с нормальными векторами
называется нормальным вектором плоскости. Если даны две плоскости с нормальными векторами 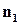 и
и 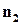 , то косинус угла между этими плоскостями определяется по формуле (этот угол всегда острый или прямой)
, то косинус угла между этими плоскостями определяется по формуле (этот угол всегда острый или прямой)
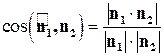 .
.
Если даны три точки 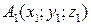 ,
, 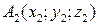 и
и 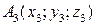 , то уравнение плоскости, проходящей через три точкинаходится по формуле:
, то уравнение плоскости, проходящей через три точкинаходится по формуле:
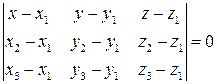 .
.
Задание 1.По координатам вершины пирамиды 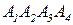 найти:
найти:
1. длину ребер 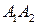 и
и 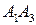 ;
;
2. угол между ребрами 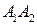 и
и 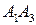 ;
;
3. площадь грани 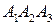 ;
;
4. объем пирамиды 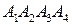 ;
;
5. уравнение прямых 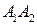 ;
; 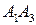 ;
;
6. уравнения плоскостей 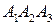 и
и 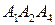 ;
;
7. угол между плоскостями 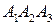 и
и 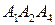 .
.
Пример. Выполнить задание 1, если 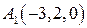 ,
, 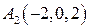 ,
, 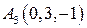 ,
, 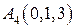 .
.
1) Если заданы точки 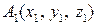 ,
, 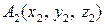 , и
, и 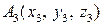 то координаты векторов
то координаты векторов 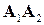 ,
, 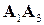 и их длины
и их длины 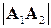 ,
, 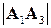 равны:
равны:
а) 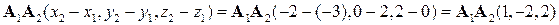 ,
,
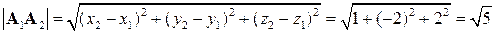 .
.
б) 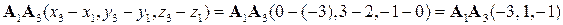 ,
,
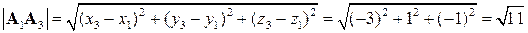 .
.
2) Угол между ребрами 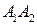 и
и 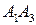 находим как угол между векторами
находим как угол между векторами 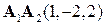 и
и 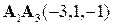 . Из определения скалярного произведения следует, что этот угол вычисляется по формуле:
. Из определения скалярного произведения следует, что этот угол вычисляется по формуле:
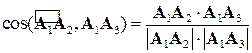 .
.
Скалярное произведение 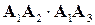 находим через декартовы координаты:
находим через декартовы координаты:
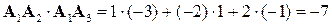 .
.
Тогда
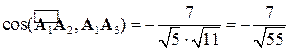 .
.
Откуда (вычисления проводим на инженерном калькуляторе)
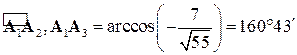
3) 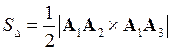 ‑ площадь треугольника, построенного на векторах
‑ площадь треугольника, построенного на векторах 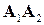 и
и 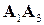 . Зная их декартовы координаты, находим векторное произведение
. Зная их декартовы координаты, находим векторное произведение
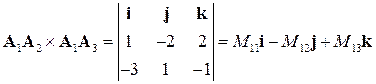 ,
,
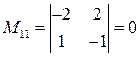 ,
, 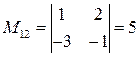 ,
, 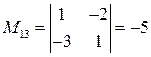 .
.
Тогда
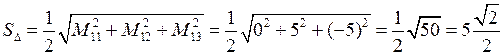 .
.
4) Учитывая геометрический смысл смешанного произведения векторов, получим формулу для вычисления объема пирамиды:
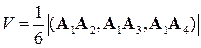 .
.
Найдем координаты вектора 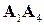 :
:
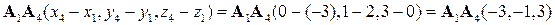
Смешанное произведение этих векторов найдем через их декартовы координаты
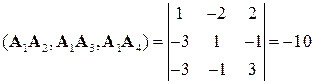 .
.
Отсюда
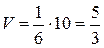 .
.
5) Найдем канонические уравнение прямых 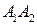 и
и 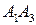 . За направляющие вектора примем вектора
. За направляющие вектора примем вектора 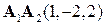 и
и 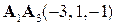 . За точку лежащую на этих векторах примем точку
. За точку лежащую на этих векторах примем точку 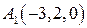
прямая 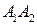 :
: 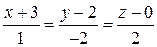 ;
;
прямая 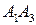 :
: 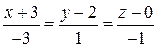 .
.
6) Уравнение плоскости, проходящей через три точки 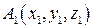 ,
, 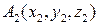 и
и 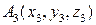 находится по формуле:
находится по формуле:
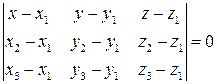 .
.
Составимуравнение плоскости, проходящей через три точки 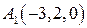 ,
, 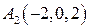 ,
, 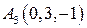 .
.
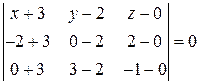 или
или 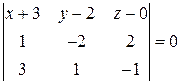 .
.
Разложив определить по первой строке, получим
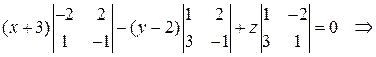
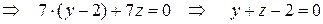 .
.
Итак, уравнение плоскости  найдено
найдено 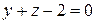 . Коэффициенты уравнения образуют нормальный вектор
. Коэффициенты уравнения образуют нормальный вектор 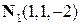 .
.
Аналогично составимуравнение плоскости, проходящей через три точки 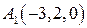 ,
, 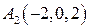 ,
, 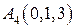 .
.
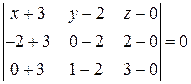 или
или 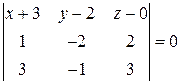 .
.
Разложив определить по первой строке, получим
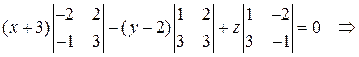
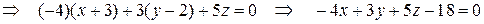 .
.
Итак, уравнение плоскости 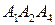 имеет вид
имеет вид 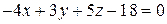 . Коэффициенты уравнения образуют нормальный вектор
. Коэффициенты уравнения образуют нормальный вектор 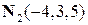 .
.
7) Угол 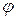 , образованный двумя плоскостями
, образованный двумя плоскостями 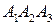 и
и 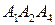 находится по формуле
находится по формуле
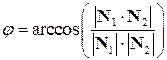 , где
, где 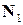 и
и 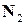 ‑ нормали плоскостей
‑ нормали плоскостей 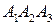 и
и 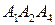 .
. 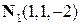
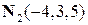
Подставляя их значения из пункта 6) находим величину угла 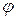 (расчеты выполняем на инженерном калькуляторе)
(расчеты выполняем на инженерном калькуляторе)
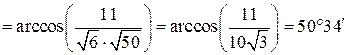
Задание №2
а) Найти решение системы с помощью правила Крамера;
б) Записать систему в матричной форме и решить средствами матричного исчисления.
Пример.
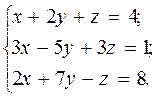
а) Составим и вычислим главный и вспомогательные определители системы:
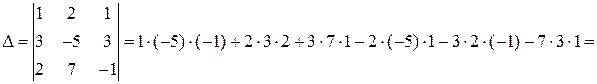
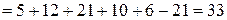 ,
,
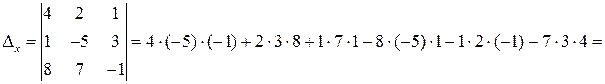
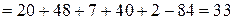 ,
,
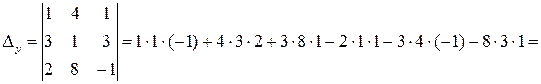
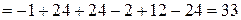 ,
,
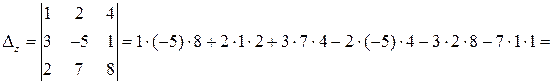
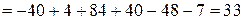 .
.
Находим по правилу Крамера решение системы
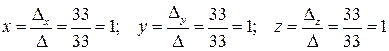 .
.
б) Составим матрицу коэффициентов системы и столбец правых частей
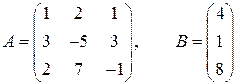 ,
,
и найдем обратную матрицу по формуле:
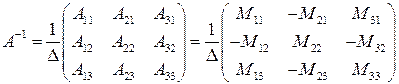 ,
,
где 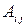 и
и 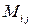 ‑ соответственно алгебраические дополнения и миноры, связанные между собой соотношением
‑ соответственно алгебраические дополнения и миноры, связанные между собой соотношением 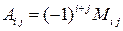 , а
, а 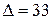 - определитель матрицы
- определитель матрицы 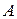 , вычисленный в пункте а). Найдем миноры:
, вычисленный в пункте а). Найдем миноры:
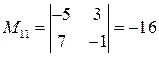 ;
; 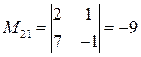 ;
; 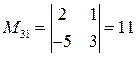 ;
;
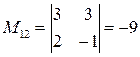 ;
; 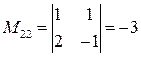 ;
; 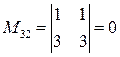 ;
;
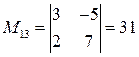 ;
; 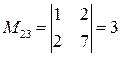 ;
; 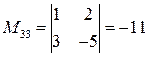 .
.
Составим теперь обратную матрицу
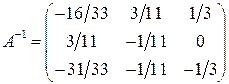
и найдем столбец неизвестных по формуле 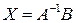 :
:
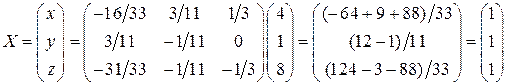 .
.
Отсюда 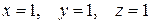 .
.
Задание №3. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления
При вычислении предела дробно-рациональной функции при 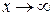 числитель и знаменатель дроби — величины бесконечно большие, т.е. получаем выражение
числитель и знаменатель дроби — величины бесконечно большие, т.е. получаем выражение 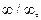 которое представляет собой неопределённость. Для вычисления предела этой функции нужно числитель и знаменатель дроби разделить на наивысшую степень
которое представляет собой неопределённость. Для вычисления предела этой функции нужно числитель и знаменатель дроби разделить на наивысшую степень 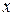 .
.
Пример 1. 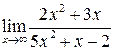 .
.
Для вычисления предела этой функции нужно числитель и знаменатель разделить на 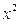 :
:
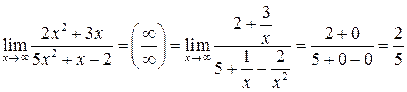 .
.
(при 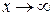 слагаемые
слагаемые 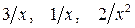 — величины бесконечно малые и, следовательно, их пределы равны нулю).
— величины бесконечно малые и, следовательно, их пределы равны нулю).
В том случае, когда при вычислении предела дробно-рациональной функции при 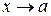 числитель и знаменатель имеют предел, равный нулю, т.е. имеем неопределенность
числитель и знаменатель имеют предел, равный нулю, т.е. имеем неопределенность 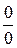 , надо разделить их на
, надо разделить их на 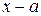 и перейти к пределу. Если после деления окажется, что при
и перейти к пределу. Если после деления окажется, что при 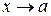 числитель и знаменатель снова имеют пределы, равные нулю, то надо произвести повторное деление на
числитель и знаменатель снова имеют пределы, равные нулю, то надо произвести повторное деление на 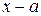 .
.
Пример 2. 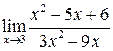 .
.
Данный предел имеет неопределенность вида 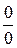 , так как числитель и знаменатель при
, так как числитель и знаменатель при 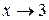 стремятся к 0. Разложим квадратные трёхчлены в числителе и знаменателе рациональной дроби на линейные множители по формуле
стремятся к 0. Разложим квадратные трёхчлены в числителе и знаменателе рациональной дроби на линейные множители по формуле 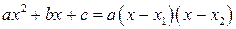 , где
, где 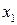 и
и 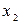 — корни квадратного трёхчлена
— корни квадратного трёхчлена
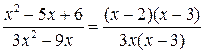 .
.
Сократив рациональную дробь на  , получим:
, получим:
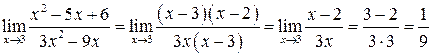 .
.
При вычислении пределов тригонометрических функций часто используется первый замечательный предел
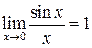
и его следствия:
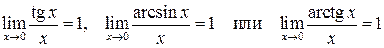 .
.
Пример 3. 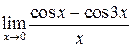 .
.
Преобразовав разность косинусов в произведение, получим
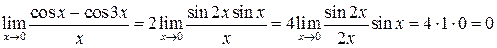 .
.
Если в пределе встречается неопределенность 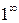 , то используется второй замечательный предел
, то используется второй замечательный предел 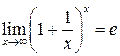 или
или 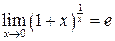 .
.
Пример 4. 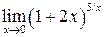 .
.
Выполнив преобразования и применив второй замечательный предел, найдём
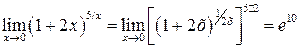 .
.
Пример 5. 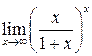 .
.
Выполнив преобразования и применив формулу 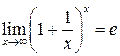 , найдём
, найдём
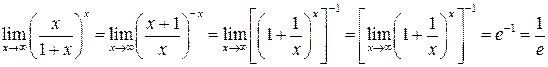 .
.
Задание №4.Исследовать функцию на непрерывность. Найти точки разрыва функции и определить их тип.
Функция 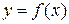 называется непрерывной в точке
называется непрерывной в точке 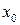 , если предел функции в этой точке равен значению функции в этой точке, т.е.
, если предел функции в этой точке равен значению функции в этой точке, т.е.
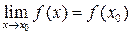 .
.
Это равенство означает выполнение трех условий:
1) функция 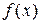 определена в точке х0 и ее окрестности;
определена в точке х0 и ее окрестности;
2) функция 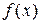 имеет предел при
имеет предел при 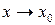 ;
;
3) предел функции в точке 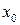 равен значению функции в этой точке
равен значению функции в этой точке
Если в точке 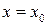 не выполняется по крайней мере одно из условий определения непрерывности функции, то такая точка называется точкой разрыва. Все точки разрыва разделяются на точки разрыва первого и второго рода.
не выполняется по крайней мере одно из условий определения непрерывности функции, то такая точка называется точкой разрыва. Все точки разрыва разделяются на точки разрыва первого и второго рода.
Точка разрыва х0 называется точкой разрыва первого рода функции 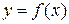 , если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е.
, если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е. 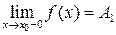 и
и 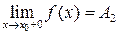 .
.
При этом:
1) если 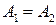 , то точка х0 называется точкой устранимого разрыва;
, то точка х0 называется точкой устранимого разрыва;
2) если 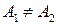 , то х0 называется точкой конечного разрыва, а величину
, то х0 называется точкой конечного разрыва, а величину 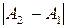 называют скачком функции.
называют скачком функции.
Точка разрыва х0 называется точкой разрыва второго рода функции 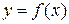 , если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.
, если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.
Пример.
Дана функция 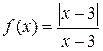 . Найти точки разрыва, определить их тип.
. Найти точки разрыва, определить их тип.
Функция 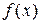 определена и непрерывна на всей числовой оси, кроме точки
определена и непрерывна на всей числовой оси, кроме точки 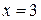 . Очевидно, что
. Очевидно, что
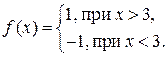 .
.
Следовательно 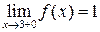 ,
, 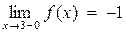 . Поэтому в точке
. Поэтому в точке 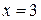 функция имеет разрыв первого рода. Скачок функции в этой точке равен
функция имеет разрыв первого рода. Скачок функции в этой точке равен 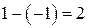 .
.
Задание №5.Найти производные первого порядка данных функций, используя правила дифференцирования.
При выполнении данного задания необходимо знать правила дифференцирования (производная суммы, произведения и частного двух функций), а также изучить таблицу производных.
Пример.
1) 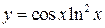 .
.
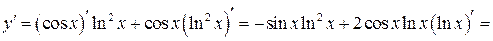
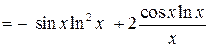 .
.
2) 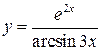 .
.
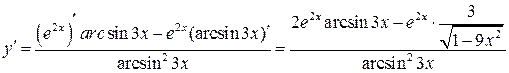 .
.
3) 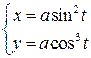 Найти
Найти 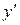 .
.
Производная функции, заданной параметрически, вычисляется по формуле: 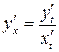 .
.
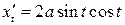 ;
; 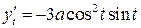 .
.
Тогда 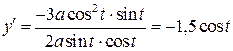 .
.
Задание №6.Составить уравнения касательной и нормали к графику функции 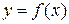 , проведенных в данной точке
, проведенных в данной точке 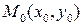 .
.
Приведем уравнение касательной, проведенной к графику функции 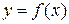 в точке
в точке 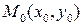
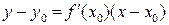 ,
,
и уравнение нормали к этой касательной
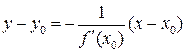 .
.
Пример.
Для функции 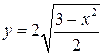 в точке с абсциссой
в точке с абсциссой 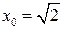 составить уравнение касательной и уравнение нормали.
составить уравнение касательной и уравнение нормали.
1) Найдем значение функции 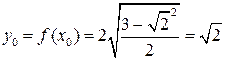 .
.
2) Найдем значение 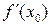 :
:
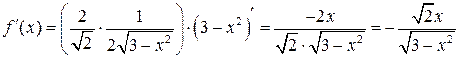 ,
, 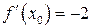 .
.
3) Составим уравнения касательной и нормали:
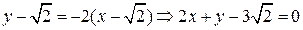 – искомое уравнение касательной;
– искомое уравнение касательной;
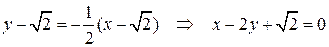 – искомое уравнение нормали.
– искомое уравнение нормали.
Задание №7.Найти предел функции с помощью правила Лопиталя.
Напомним правило Лопиталя для раскрытия неопределенностей вида 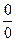 и
и 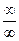 :
:
Пусть 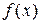 и
и 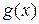 – функции, имеющие производные в некоторой окрестности точки
– функции, имеющие производные в некоторой окрестности точки 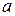 , за исключением, быть может, самой
, за исключением, быть может, самой 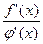 точки
точки 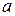 . Пусть при стремлении
. Пусть при стремлении 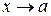 обе эти функции стремятся одновременно к нулю или к бесконечности. Тогда, если существует предел отношения их производных
обе эти функции стремятся одновременно к нулю или к бесконечности. Тогда, если существует предел отношения их производных 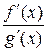 при
при 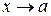 , то существует и предел отношения самих функций
, то существует и предел отношения самих функций 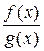 при
при 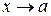 , причем оба эти пределы равны:
, причем оба эти пределы равны:
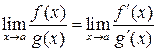 .
.
Замечания:
1) Правило Лопиталя остается справедливым и в том случае, если 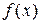 и
и 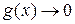
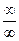
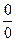 или
или 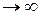 при
при 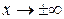 или при
или при 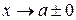 .
.
2) Если 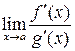 опять дает неопределенность вида
опять дает неопределенность вида 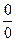 или
или 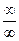 , то правило Лопиталя следует применить еще раз.
, то правило Лопиталя следует применить еще раз.
Примеры:
1) 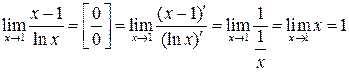 .
.
2) 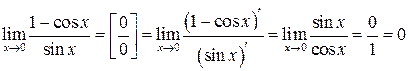 .
.
3) 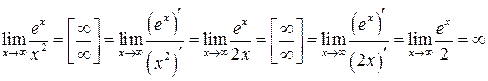 .
.
Задание №8. Построить график функции 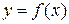 , используя общую схему исследования функций.
, используя общую схему исследования функций.
Общая схема исследования функции и построения графика.
1. Найти область определения функции.
2. Определить тип функции (четность, нечетность).
3. Найти точки пересечения с осями координат и интервалы знакопостоянства функции.
4. Найти асимптоты графика функции:
а) вертикальные; б) невертикальные (наклонные).
5. Найти точки возможного экстремума и интервалы возрастания и убывания функции.
6. Найти точки перегиба и интервалы выпуклости, вогнутости функции.
7. Построить график функции, учитывая проведенные исследования.
Пример. Построить график функции 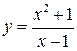 .
.
1. Областью определения функции является множество всех действительных чисел, кроме 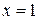 (в этом случае знаменатель равен нулю).
(в этом случае знаменатель равен нулю).
2. Для определения типа функции найдем значение
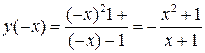 .
.
Следовательно, функция 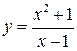 не является ни четной ни нечетной.
не является ни четной ни нечетной.
3. Так как уравнение 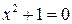 не имеет действительных корней, то график функции не имеет точек пересечения с осью ОХ, но пересекает ось ОУ в точке
не имеет действительных корней, то график функции не имеет точек пересечения с осью ОХ, но пересекает ось ОУ в точке 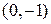 .
.
Определим интервалы знакопостоянства функции:
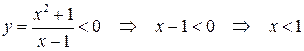 .
.
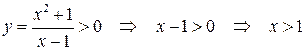 .
.
 4. Найдем асимптоты графика функции.
4. Найдем асимптоты графика функции.
а) Исследуем поведение функции вблизи точки разрыва 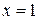 :
:
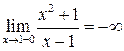 ,
, 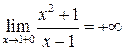 .
.
Следовательно прямая 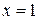 является вертикальной асимптотой.
является вертикальной асимптотой.
б). Определим существование наклонной асимптоты:
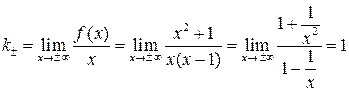 ,
,
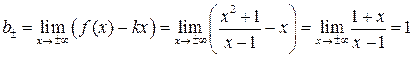 .
.
Следовательно, график функции имеет наклонную асимптоту 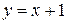 при
при  .
.
5. Для нахождения точек возможного экстремума найдем производную функции:
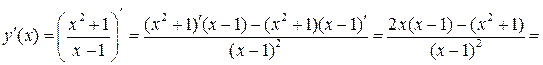
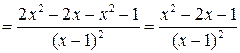 .
.
Приравняем 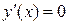 . Решая уравнение
. Решая уравнение 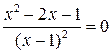 , находим корни производной
, находим корни производной 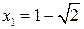 и
и 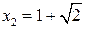 .
.
Исследуем знак производной. Для чего решим неравенство 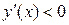
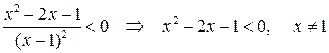
Находим знаки 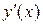 на промежутках, учитывая корни
на промежутках, учитывая корни 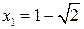 и
и 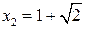 квадратного трехчлена
квадратного трехчлена 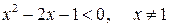 :
:
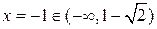 ,
, 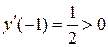 ;
; 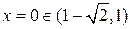 ,
, 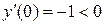 ;
;
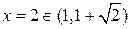 ,
, 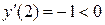 ;
; 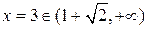 ;
; 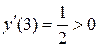 .
.
Следовательно, функция возрастает на промежутках
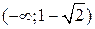 и
и 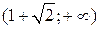 ,
,
и убывает на промежутках
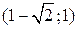 и
и 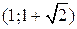 .
.
По изменению знака 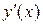 получаем точки локальных экстремумов:
получаем точки локальных экстремумов:
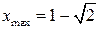 ,
, 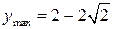 ,
,
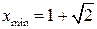 ,
, 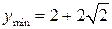 .
.
6. Для нахождения точек перегиба и интервалов выпуклости, вогнутости найдем вторую производную функции:
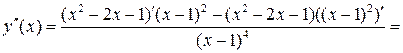
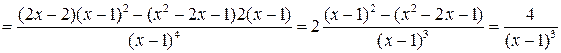 .
.
Так как 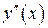 в нуль не обращается, то точек перегиба у функции нет.
в нуль не обращается, то точек перегиба у функции нет.
Исследуем знак второй производной, решая неравенство 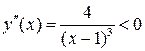 :
:
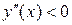 при
при 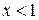 и
и 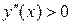 при
при 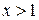 .
.
 Следовательно, на интервале
Следовательно, на интервале 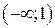 график направлен выпуклостью вверх (выпуклый), а на интервале
график направлен выпуклостью вверх (выпуклый), а на интервале 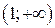 – выпуклостью вниз (вогнутый).
– выпуклостью вниз (вогнутый).
По результатам исследования строим график функции 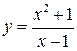 .
.
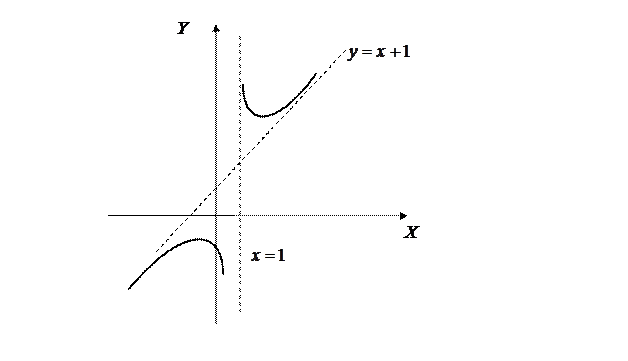
Рис.1 Построение графика функции 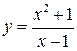 .
.

Задание №9.Найти неопределенные интегралы.
Пример. Найти неопределенные интегралы.
а) 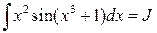 .
.
Применим подстановку 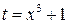 . Тогда
. Тогда 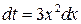 , откуда
, откуда 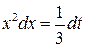 .
.
Таким образом, 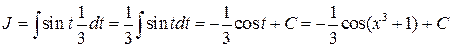
б) 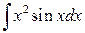 .
.
Применим формулу интегрирования по частям 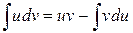 . Пусть
. Пусть
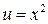 ,
, 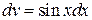 , тогда
, тогда 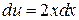 ,
, 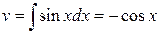 .
.
Тогда
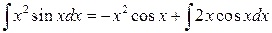 .
.
К интегралу в правой части снова применяем формулу интегрирования по частям. Пусть
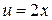 ,
, 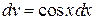 ,
, 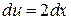 ,
, 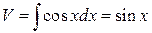
Таким образом,
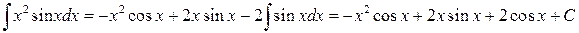 .
.
в) 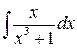
Подынтегральная функция является правильной рациональной дробью, знаменатель которой
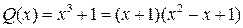 .
.
Подынтегральную функцию разложим на дроби
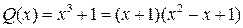 ,
,
откуда
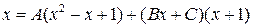 .
.
Раскроем скобки в правой части и приведем подобные:
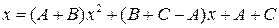 .
.
Приравнивая соответствующие коэффициенты при 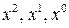 в левой и правой частях последнего равенства получим систему трех уравнений:
в левой и правой частях последнего равенства получим систему трех уравнений:
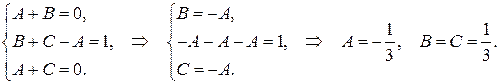
Таким образом,
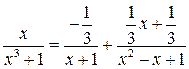 ,
,
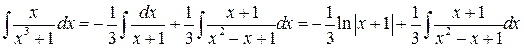 .
.
Вычислим отдельно интеграл 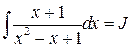 . Используя равенства
. Используя равенства
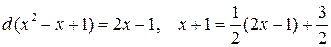 ,
,
получаем
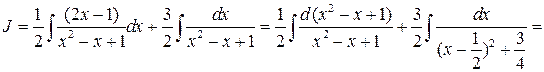
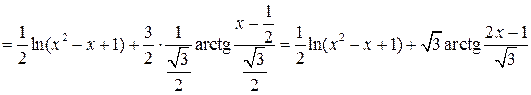 .
.
Отсюда окончательно вычисляем интеграл
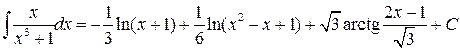 .
.
г) 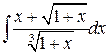 .
.
Наименьшее общее кратное показателей корней равно 6, поэтому выполним подстановку 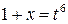 ,
, 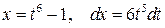 , тогда
, тогда
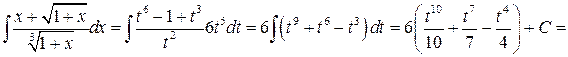
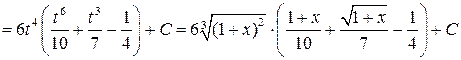 .
.
