Анализ устойчивости по виду корней характеристического

уравнения:

Запишем характеристическое уравнение в виде:
a₀pⁿ+a₁p^n-1+…+a_n = 0

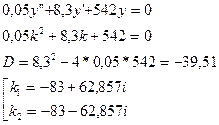
Корни характеристического уравнения – комплексно-сопряженные. Вещественная часть всех корней – отрицательная, следовательно система устойчива.

Анализ устойчивости системы с помощью критерия устойчивости

Гурвица:

Для системы n-го порядка из коэффициентов характеристического уравнения составляют определитель Гурвица n-го порядка и определяют его миноры.

Имеем дифференциальное уравнение второго порядка, следовательно определитель Гурвица также будет иметь второй порядок

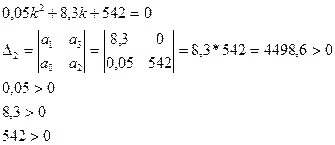
В соответствии с формулировкой критерия Гурвица, для того, чтобы все корни характеристического уравнения имели отрицательную вещественную часть, необходимо и достаточно, чтобы определитель Гурвица n-го порядка и все его миноры были положительны. Это условие выполняется, значит система устойчива.

Анализ устойчивости системы с помощью критерия устойчивости

Михайлова:
В соответствии с формулировкой критерия устойчивости Михайлова, для того, чтобы система была устойчивой необходимо и достаточно, чтобы годограф характеристического вектора начинаясь на положительной оси при изменении значения ω от 0 до ∞ проходил в положительном направлении последовательно столько квадрантов, каков порядок характеристического уравнения.

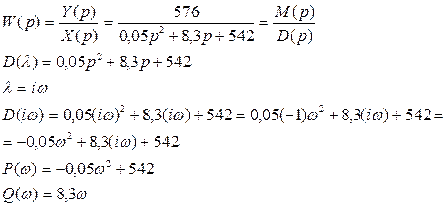
Получим различные значения вещественной и мнимой частей для различных частот:

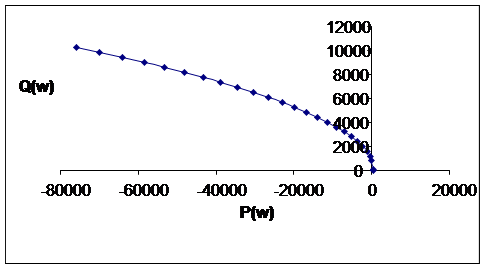
Фрагмент годографа в увеличенном масштабе:

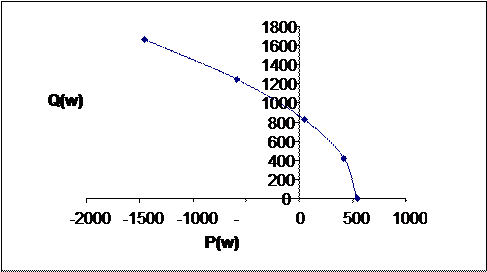
График проходит через через 2 квадранта, что соответствует порядку характеристического уравнения, а значит система устойчива.

Анализ устойчивости системы с помощью критерия устойчивости

Найквиста:

Критерий устойчивости Найквиста определяет условия, которым должна удовлетворять АФЧХ разомкнутой системы, чтобы система была устойчивой.

Структурная схема разомкнутой системы:

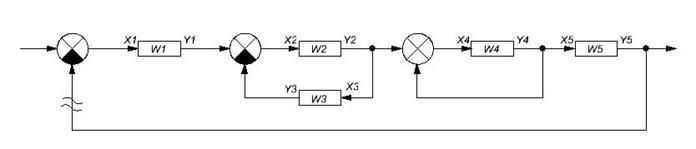
Передаточная функция разомкнутой систмы и меет вид:

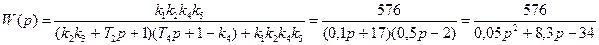
Составим дифференциальное уравнение разомкнутой системы:

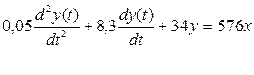
Запишем характеристическое уравнение:

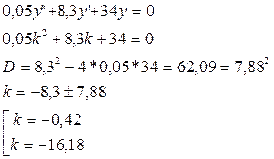
Оба корня характеристического уравнения отрицательны, что свидетельствует о том, что система с разомкнутой обратной связью устойчива.

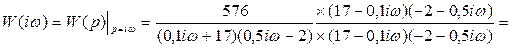
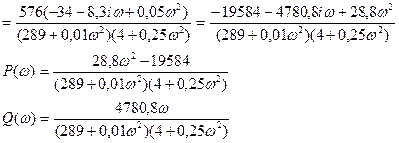
Построим график АФЧХ:

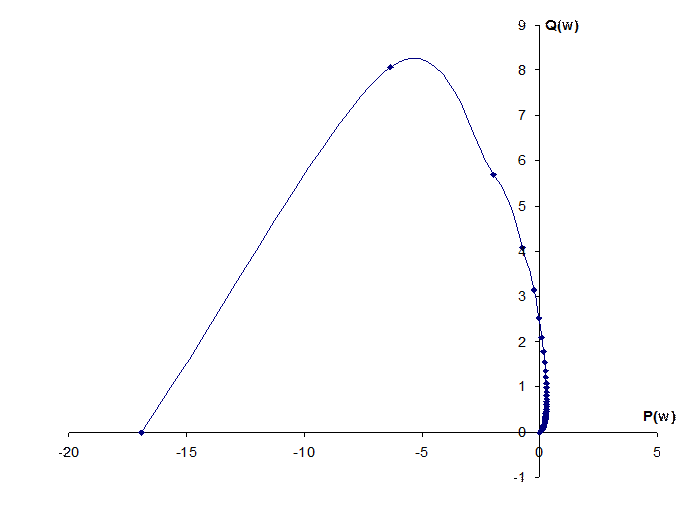
Видно, что график АФЧХ разомкнутой системы охватывает точку с координатами (-1;0), а значит, система с разорванной обратной связью будет неустойчива.

Вывод

Использованная литература:

1) Очина Л.Б., Жданова А.С., Лукьянов А.С.; «Основы теории управления. Методические указания к выполнению курсовой работы»; СПб, типография ФГОУ ВПО СПГУВК, 2007г..

2) Бесекерский В.А., Попов Е.П.; «Теория систем автоматического управления»; СПб, Профессия 2007г..

3) Очина Л.Б.; конспект лекций; 2008г..

Приложение

Таблица значений, использованная для построения годографа Михайлова:

w	0	50	100	150	200	250	300	350	400	450	500	550	600
P(w)	542	417	42	-583	-1458	-2583	-3958	-5583	-7458	-9583	-11958	-14583	-17458
Q(w)	0	415	830	1245	1660	2075	2490	2905	3320	3735	4150	4565	4980
w	650	700	750	800	850	900	950	1000	1050	1100	1150	1200	1250
P(w)	-20583	-23958	-27583	-31458	-35583	-39958	-44583	-49458	-54583	-59958	-65583	-71458	-77583
Q(w)	5395	5810	6225	6640	7055	7470	7885	8300	8715	9130	9545	9960	10375

Таблица значений, использованная для построения графика АФЧХ разомкнутой системы:

ω
P(ω)	-16,9412	-1,98621	-0,26464	0,092846	0,21503	0,265389	0,286236	0,292574	0,290944	0,284651	0,275565	0,264835	0,253206	0,241179	0,229098	0,217197	0,205633	0,194511	0,183893	0,173815
Q(ω)		5,684661	3,137831	2,101697	1,551956	1,210292	0,976338	0,80562	0,675478	0,573138	0,490814	0,423458	0,367628	0,320879	0,281408	0,247855	0,219166	0,194511	0,173226	0,154775
ω
P(ω)	0,164291	0,155319	0,146887	0,138979	0,13157	0,124636	0,118149	0,112083	0,10641	0,101103	0,096139	0,091493	0,087142	0,083065	0,079243	0,075658	0,072291	0,069128	0,066154	0,063355
Q(ω)	0,13872	0,124698	0,112413	0,101613	0,09209	0,083669	0,0762	0,069559	0,063638	0,058345	0,053602	0,049342	0,045507	0,042047	0,038918	0,036084	0,03351	0,031169	0,029036	0,027088
ω
P(ω)	0,060719	0,058235	0,055892	0,053679	0,051589	0,049613	0,047743	0,045972	0,044293	0,042701	0,04119	0,039755	0,038391	0,037093	0,035858	0,034682	0,03356	0,032491	0,03147	0,030496
Q(ω)	0,025306	0,023674	0,022176	0,020799	0,019532	0,018363	0,017284	0,016287	0,015363	0,014507	0,013712	0,012974	0,012286	0,011646	0,011049	0,010491	0,00997	0,009482	0,009025	0,008597
ω
P(ω)	0,029565	0,028674	0,027823	0,027008	0,026227	0,025479	0,024761	0,024073	0,023413	0,022779	0,022169	0,030496	0,029565	0,028674	0,027823	0,027008	0,026227	0,025479	0,024761	0,024073
Q(ω)	0,008195	0,007817	0,007463	0,007128	0,006814	0,006517	0,006238	0,005973	0,005724	0,005488	0,005265	0,008597	0,008195	0,007817	0,007463	0,007128	0,006814	0,006517	0,006238	0,005973
ω
P(ω)	0,024073	0,023413	0,022779	0,022169	0,021584	0,021021	0,020479	0,019957	0,019455	0,018971	0,018505	0,018056	0,017622	0,017204	0,0168	0,01641	0,016033	0,015669	0,015317	0,014976
Q(ω)	0,005973	0,005724	0,005488	0,005265	0,005053	0,004853	0,004663	0,004482	0,004311	0,004149	0,003994	0,003847	0,003707	0,003574	0,003446	0,003325	0,00321	0,003099	0,002994	0,002893
ω														∞
P(ω)	0,014976	0,014647	0,014328	0,014019	0,01372	0,013431	0,01315	0,012878	0,012615	0,012359	0,012111	0,01187	0,011636
Q(ω)	0,002893	0,002797	0,002705	0,002617	0,002533	0,002452	0,002375	0,002301	0,002229	0,002161	0,002096	0,002033	0,001972