Элементарными функциями?
Существует 7классов простейших элементарных функций:
1. Целая рациональная функция (многочлен)
y = Pn(x) = anxn+ an – 1xn – 1+ … + a1x + a0 ,
где 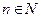 , ai – коэффициенты многочлена (действительные числа), X = (–∞; ∞). Множество значений многочлена зависит от его коэффициентов. Простейшими рациональными функциями являются:
, ai – коэффициенты многочлена (действительные числа), X = (–∞; ∞). Множество значений многочлена зависит от его коэффициентов. Простейшими рациональными функциями являются:
y = kx + b – линейная функция,
y = ax2 + bx + c – квадратный трехчлен.
2. Дробно-рациональная функция (отношение двух многочленов)
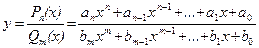 .
.
Функция определена при всех действительных x, за исключением точек, в которых Q(x) = 0.
Простейшей функцией этого класса является
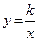 ,
, 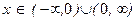 .
.
3. Степенная функция
y = x λ , где 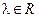 .
.
Область определения и множество значений зависят от показателя степени λ . Примеры степенных функций:
y = x2 , X = (–∞; ∞) , Y = [0; ∞);
y = x3 , X = (–∞; ∞) , Y = (–∞; ∞);
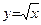 или y = x1/2 , X = [0; ∞) , Y = [0; ∞);
или y = x1/2 , X = [0; ∞) , Y = [0; ∞);
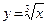 или y = x1/3 , X = (–∞; ∞), Y = (–∞; ∞);
или y = x1/3 , X = (–∞; ∞), Y = (–∞; ∞);
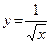 или y = x – 1/2 , X = (0; ∞) , Y = (0; ∞).
или y = x – 1/2 , X = (0; ∞) , Y = (0; ∞).
4. Показательная функция
y = ax , где a>0 , a≠1, X = (–∞; ∞) , Y = (0; ∞);
y = ex , где e=2.718281828459045…,
X = (–∞; ∞), Y = (0; ∞).
5. Логарифмическая функция
y = loga x, где a>0 , a≠1,
X = (0; ∞), Y = (–∞; ∞);
y = ln x, основанием логарифма, в этом случае, является число e. Такой логарифм называют натуральным.
X = (0; ∞), Y = (–∞; ∞);
y = lg x, основанием логарифма является число 10. Такой логарифм называют десятичным.
X = (0; ∞), Y = (–∞; ∞).
6. Тригонометрические функции
y = sin x, X = (–∞; ∞), Y = [–1;1];
y = cos x, X = (–∞; ∞), Y = [–1;1];
y = tg x, 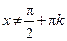 , Y = (–∞; ∞);
, Y = (–∞; ∞);
y = ctg x, x ≠ πk, Y = (–∞; ∞).
7 Обратные тригонометрические функции
y = arcsin x, X =[–1;1], 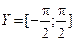 ;
;
y = arccos x, X =[–1;1], Y = [0; π];
y = arctg x, X = (–∞; ∞) , 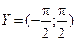 ;
;
y = arcctg x, X = (–∞; ∞) , Y = (0; π).
Функции классов 1–3 принято называть алгебраическими. Функции классов 4–7 называются трансцендентными.
Графический обзор простейших элементарных функций
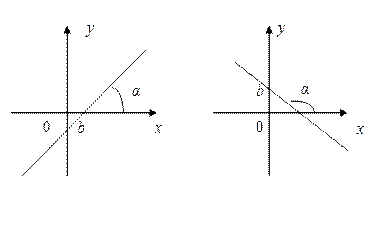
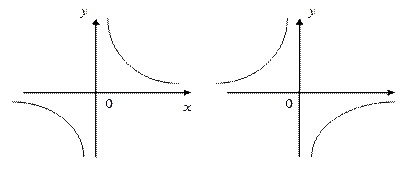
y = kx+b, k>0 y = kx+b, k<0
|
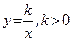
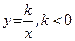
|
y = ax2+bx+c , D = b2 – 4ac
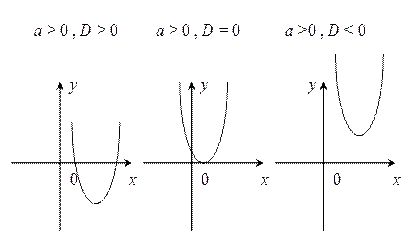
|
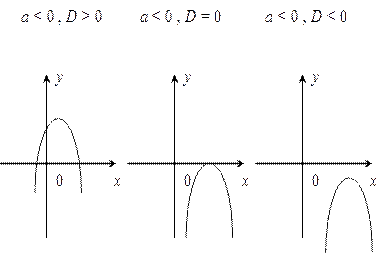
|
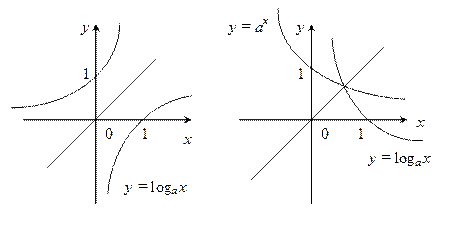
y = a x, y = loga x, a >1 y = ax, y = loga x , 0 <a < 1
|
y = sin x
|
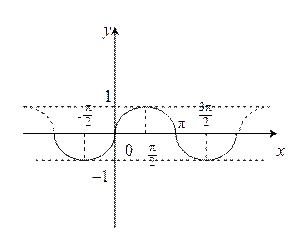
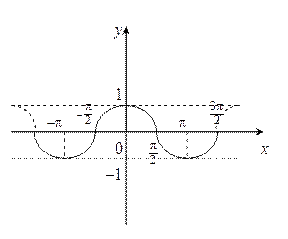
y = cos x
|
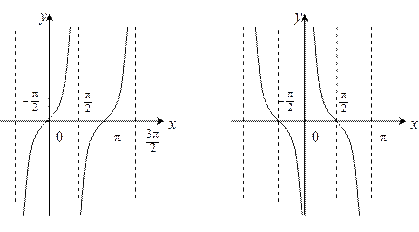
y = tg xy = ctg x
|
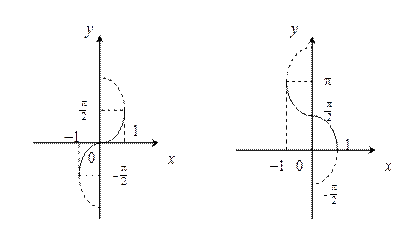
y = arcsin x y = arcos x
|
y =arctg x y = arcctg x
|
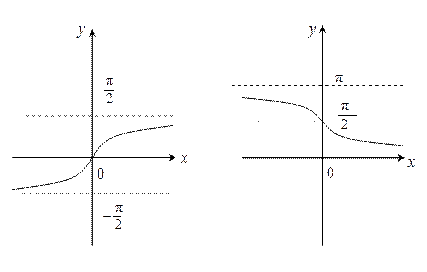
1.6. Известен график функции y = f(x). Как построить графики функций y = f(x+a), y = f(x)+b, y = f(k ∙ x), y = k ∙ f(x) ?
График функции y = f(x+a) получается из графика функции y = f(x) его параллельным сдвигом вдоль оси Ox на 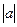 единиц влево при a >0 и вправо при a < 0.
единиц влево при a >0 и вправо при a < 0.
График функции y = f(x)+b получается из графика функции y = f(x) его параллельным сдвигом вдоль оси Oy на 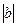 единиц вверх при b >0 и вниз при b < 0.
единиц вверх при b >0 и вниз при b < 0.
График функции y = f(k ∙ x), k > 0 получается из графика функции y = f(x) его сжатием к оси Oy в k раз при k > 1 и растяжением в 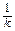 при k < 1.
при k < 1.
График функции y = k ∙ f(x), k > 0 получается из графика функции y = f(x) его растяжением от оси Ox в k раз при k > 1 и сжатием к оси Ox в 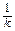 при k < 1.
при k < 1.
Пример 1.Построить график функции
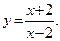
Решение.Преобразуем функцию таким образом, чтобы можно было воспользоваться графиком функции 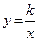 :
:
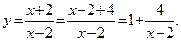
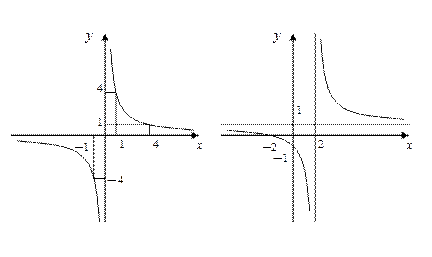
График заданной функции получим, если гиперболу 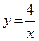 (рис. 1.21) сместим вдоль оси Ox вправо на две единицы и затем сдвинем полученный график вверх вдоль оси Oy на одну единицу (рис. 1.22).
(рис. 1.21) сместим вдоль оси Ox вправо на две единицы и затем сдвинем полученный график вверх вдоль оси Oy на одну единицу (рис. 1.22).
|
Пример 2.Построить график функции 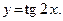
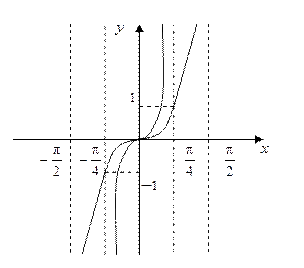
Решение.График данной функции получится путем сжатия к оси Oy в 2 раза графика функции 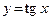 (рис. 1.23).
(рис. 1.23).
|
