Проблемы отбора совокупности обследования

Способы изучения стохастических связей в анализе хозяйственной деятельности

8.1. Сфера и цели применения стохастического анализа

8.2. Проблемы отбора совокупности обследования

8.3. Этапы корреляционного моделирования

8.4. Формирование статистической совокупности для исследований

8.5. Установление математической формы связи между изучаемыми признаками

8.6. Анализ характеристик корреляционной модели

8.7. Основные направления использования

корреляционных моделей

Сфера и цели применения стохастического анализа

Изучение различных сторон производства на основе диалектического познания предполагает отражение изучаемого явления как в его взаимосвязи с другими явлениями, так и в его развитии, динамике.

Любой объект в производстве, любое явление находится в многообразных условиях и связях с влияющими на него факторами, с одной стороны, с другой – постоянно развивается и меняется. Математически отобразить присущие явлениям и процессам взаимосвязи можно на основе корреляционного моделирования. В результате чего находят такое алгебраическое уравнение (уравнение корреляционной зависимости), которое наиболее близко воспроизводит изучаемый производственный процесс или явление. Полученное уравнение регрессии отражает существующие между признаками корреляционные связи.

Суть их заключается в том, что значениям независимого признака (аргумента) соответствуют не определенные значения признака (функции), как при функциональных связях, а распределение значений признака, причем существующее отношение связи может проявиться лишь в изменении их средних величин.

Построению корреляционных моделей предшествует тщательный теоретический анализ с целью выявления причинно-следственных взаимосвязей модулируемого процесса. Ибо даже рассчитанная корреляционная связь может не выражать причинно-следственных связей, но в ряде случаев свидетельствовать об их наличии.

Поэтому на этапе теоретического анализа следует разобраться в экономической сущности исследуемого процесса, его месте среди других экономических процессов и его причинных связях. Уяснив качественную сторону изучаемых закономерностей, переходят к выявлению их качественной стороны на основе корреляционного моделирования.

Проблемы отбора совокупности обследования

Результаты корреляционного моделирования в значительной мере определяются качеством исходной информации. В связи с этим информационная база должна отвечать определенным требованиям.

Прежде всего, должно быть учтено действие закона больших чисел, гласящего, что все закономерности формируются и проявляются при большом числе единиц совокупности. Следовательно, чтобы статистические характеристики, получаемые при корреляционном моделировании, были достаточно типичными и надежными, нужно чтоб исходная совокупность была достаточно большой.

Теоретически минимальной границей числа наблюдений служит количество параметров в уравнении регрессии, однако при такой численности совокупности нельзя определить надежность получаемых характеристик регрессионной модели. Для установления оптимальной численность исходной совокупности рекомендуется соблюдать следующие соотношения: численность наблюдений должна в 5-6 раз превышать количество параметров уравнения.

Важным требованием к исходной совокупности является обеспечение его однородности. В этом направлении большую помощь может оказать статистическая группировка, позволяющая выделить качественно однородные группы. Качественно однородная совокупность позволяет выразить наиболее типичные черты генеральной совокупности, т.к. качественная однородность предполагает близость условий формирования и факторов её определяющих. В этой связи необходима однородность сельскохозяйственных предприятий по природно-климатическим условиям формирования урожая, по специализации. Из выборки следует исключить хозяйства, экономические показатели которых значительно отличаются от показателей основной массы обследуемого предприятия.

При корреляционном моделировании информационная база может быть подготовлена двумя путями: экспериментальным и путем обработки статистических данных. В плане качественной стороны информации предпочтение следует отдавать экспериментальному этапу подготовки данных.

Однако, экономический эксперимент связан со значительными трудностями: требует больших затрат труда, времени и средств, а иногда нарушения нормального хода производственного процесса, что влечет за собой материальные потери. В аграрно-экономических исследованиях корреляционное моделирование осуществляют главным образом на основе информации, полученной статистическим путем. Используются материалы годовой, периодической и специальной отчетности сельскохозяйственных предприятий.

Таким образом, информационная база при корреляционном моделировании представляет собой выборку из неограниченной генеральной совокупности. А в связи с этим, объект выборки должен быть таким, чтобы полученные результаты с заданной вероятностью характеризовали генеральную совокупность. Выполнить это условие часто бывает затруднительно, т.е. в экономических расчетах приходится иметь дело с совокупностями, ограниченными по числу данных. А чтобы соблюсти условие репрезентативности выборки практически для расчетов необходимо иметь не менее 20-30 наблюдений. В этом случае используют разработанные в математической статистике приёмы малой выборки.

Если число единиц наблюдения слишком мало, т.е. нарушается требование о достаточно большом объеме данных для корреляционного моделирования, то для расширения исследуемой совокупности можно использовать метод хозяйство-лет. Суть его заключена в том, что по каждому объекту совокупности (колхоз, совхоз, предприятие и т.д.) данные берут за ряд лет и рассматривают как данные отдельного хозяйства. Например, если в районе 9 колхозов, то взяв данные за три года, мы увеличим совокупности в три раза – до 27 хозяйств-лет. Использование этого метода позволяет довести совокупность до необходимого числа единиц, которое, как уже отмечалось, должно быть в 5-6 раз больше количества включаемых в модель факторов.

Специфическим требованием при корреляционно-регрессионном анализе является то, что использование разработанных формул возможно в случае, когда исследуемые явления подчинены закону нормального распределения. В области аграрно-экономических явлений распределения, как правило, скошенные, поэтому выводы следует делать осторожно. Необходимыми требованиями корреляционно-регрессионного анализа являются такие: во-первых, наблюдения должны быть статистически независимыми; во-вторых, переменные 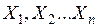должны быть линейно независимыми. Условие статистической независимости обычно нарушается при использовании метода хозяйство-лет, так как в этом случае экономические показатели последующего года зависят от предыдущего.

Таким образом, элементы совокупности не являются независимыми, а имеют так называемую автокорреляционную связь между собой. Статистика располагает методами, дающими возможность изучить и исключить влияние автокорреляции. Однако на практике в аграрно-экономических расчетах они пока что применяются редко.

Включаемые в модель факторы-аргументы часто находятся между собой в тесной взаимной связи в силу взаимообусловленности экономических показателей. Это явление получило название мультиколлинеарности. Наличие мультиколлинеарности приводит к моделям, не имеющим ясной экономической интерпретации, к пониженной устойчивости коэффициентов регрессии и других статистических характеристик, а также и к показателям влияния со знаком, противоположном ожидаемому. При наличии тесной корреляционной связи (более 0,6-0,8) между первоначально отобранными факторами, для множественного анализа рекомендуется использовать только один из двух рассматриваемых факторов, обычно тот, который имеет более высокий парный коэффициент корреляции с результативным признаком.