Глава iii модели и моделирование

РЕАЛЬНЫЙ МИР И МИР МОДЕЛЕЙ.

Особое место среди всех систем занимают модели. Они предназначены для обеспечения всех видов деятельности человека ; без моделирования вообще невозможно что-либо сделать. Особенность очевидно это на примере целенаправленной деятельности. Ведь цель субъекта, - это образ желаемого будущего, т.е. модель того, чего нет, но что хотелось бы осуществить. Далее, для достижения поставленной цели составляется план действий, но ведь это не сами действия, а их описание, т.е. модель. Итак, моделирование не является таким действием, которое можно делать, а можно и не делать; моделирование есть неизбежная, неотъемлемая, обязательная часть любой деятельности человека ( и не только человека, но об этом разговор отдельный).

В итоге модели играют роль своеобразного посредника между субъектом и реальностью. Каждый субъект создает (на исходной базе врожденных моделей и на растущей с опытом базе моделей благоприобретенных, - самостоятельно или перенимая их от других субъектов) свой собственный мир моделей, представляющий для него окружающий его реальный мир. Поэтому нет тождественных субъектов (не только индивидов, но и организаций, но и организаций, социумов и пр.): каждый субъект представлен своим индивидуальным миром моделей, по своему взаимодействуют через него и посредством него с реальностью (яркий пример - этнические различия в обществе). Конечно, это не значит, что между субъектами не может быть ничего общего; наоборот, многие их модели могут быть совпадающими или совместимыми.

Будучи системой, модель обладает всеми описанными в Главе II общесистемными свойствами. Отличительная особенность моделей от других систем - в их предназначенности отображать моделируемый оригинал, заменять его в определенном отношении, т.е. содержать и представлять информацию об оригинале. Модель является, следовательно, формой существования знаний об объекте. Другое определение модели гласит: модель есть системное отображение. Благодаря богатству смысла термина "системный", этим сказано все. Но желая сделать акцент именно на специфике систем, называемых моделями, мы должны конкретизировать описываемые общие свойства.

Это будет сделано ниже, в аналитическом и синтетическом вариантах

АНАЛИТИЧЕСКИЙ ПОДХОД К ОПИСАНИЮ МОДЕЛЕЙ.

Метод анализа требует, во-первых, определения элементов, из которых компонуется исследуемый объект, и, во-вторых, выяснения структуры объекта. Не претендуя на исчерпывающую полноту анализа, мы можем все же получить некоторые полезные сведения о моделях.

Отвечая на вопрос об элементах, из которых состоят модели, выделим два типа моделей:

1) модели, создаваемые в мозгу человека средствами мышления, - назовем их абстрактными моделями;

2) модели, создаваемые из реальных объектов и материалов, существующие как физические предметы, - назовем их реальными моделями.

АБСТРАКТНЫЕ МОДЕЛИ

Механизмы мышления весьма сложны и недостаточно изучены, чтобы определенно говорить, как возникают в нашем мозгу абстрактные модели, т.е. как мы мыслим. Известно лишь, что в процессе мышления играет роль не только сознание, но и другие системы мозга и организма в целом (дифференциация левого и правого полушарий, подсознание, интуиция, различные рефлексы, эмоции, и пр.), и что в формировании самого мышления важную роль играют взаимодействия субъекта с другими людьми. Более определенно мы можем говорить о тех абстрактных моделях, которые являются ”конечным” продуктом мышления,готовыми для передачи другим субъектам. Это модели, воплощенные средствами языка.

Язык является универсальным средством моделирования, т.к. говорить можно о чем угодно. Факторов, придающих языку универсальность, много; среди них особое значение имеет расплывчатость смысла слов. В итоге одно слово обозначает не отдельный объект, а множество объектов, притом нечетко определенное. Эта нечеткость резко сокращает необходимую размерность языковой модели. Но в ряде практических ситуаций эта расплывчатость мешает. Для снятия мешающей неопределенности строятся профессиональные подъязыки, иерархия языков со все более точными терминами, вплоть до языка математики, где расплывчатость смысла сведена до минимума (но не снята до конца!).

Иерархии языков соответствует иерархия абстрактных моделей разной степени расплывчатости.

Важно подчеркнуть,что степень неопределенности абстрактных моделей определяется не столько желанием субъекта, сколько степенью изученности объекта: чем больше мы знаем о н±м, тем более точные модели мы можем строить. Это проясняет вопрос о том, почему различные дисциплины в разной степени пользуются математическими модели: уровень формализации моделей положительно коррелирован с уровнем изученности объекта моделирования , и отрицательно - с уровнем его сложности.

КЛАССИФИКАЦИЯ КАК ПРОСТЕЙШАЯ АБСТРАКТНАЯ МОДЕЛЬ

В анализе возникает вопрос об элементарной модели. Такой простейшей абстрактной моделью является классификация. В этой модели мир максимально упрощается: все индивидуальные различия между объектами "укрупняются", квантуются по степени выраженности; все объекты, "мало" отличающиеся, объединяются в один класс, и в последующем они считаются неразличимыми между собой; признание существования "сильных" различий выражается в выделении других, отличающихся между собой классов. В результате таких упрощений получается модель, в которой мир представляется следующим образом:

1) классы, не перекрываясь между собой, полностью покрывают все множество объектов;

2) различиями внутри классов пренебрегают, различия между классами абсолютизируются;

3) для выражения разницы между классами, им присваиваются разные обозначения (имена,номера,символы);

4) идентификация объекта состоит в выяснении того, к какому классу он принадлежит (какое имя он должен носить).

Как всегда при построении моделей, субъект имеет простор для неформальных, творческих действий. Во-первых, необходимо выбрать характеристику, параметр, меру различия между объектами. Множественность характеристик является одной из причин множественности классификаций; особый (и не тривиальный) вопрос - классификация не по одному, а по нескольким параметрам. Во-вторых, необходимо определить число классов, и при заданном их числе, указать границы между ними. Рассмотрим этот вопрос чуть подробнее.Различаются два вида классификаций: искусственная (произвольная, но целевая) и естественная (кластеризация). При первой руководствуются поставленной целью, и разделение на классы слабо связано с внутренней структурой классифицируемого множества (например, деление крестьян в России в начале ХХ века на бедняков, середняков и кулаков). Второй тип классификациии учитывает природные группировки - кластеры - объектов (например, деление популяций на мужские и женские особи; классификация организмов на здоровых и больных, живых и мертвых, и т.п.).

Но самое важное - понимать. что любая классификация есть только модель реальности, что сама реальность - другая, более сложная вещь; что в жизни всегда найдется объект, который нельзя однозначно отнести к тому или иному классу.

В некоторых случаях недостатки классификации как модели становятся непреемлемыми, и тогда приходится вводить в не± улучшающие, уточняющие изменения. Так, при классификации случайных объектов или величин вводят понятие "перекрытия" распределений и связывают ошибки классификации с этим перекрытием (как разбиение границей С величины Х на классы Х₁ и Х₂, связываемые с распределениями p₁(x) и p₂(x), (см.Рис.15.) Заштрихованные области равны вероятностям ошибок).

Другой пример усовершенствования модели дает классификация объектов на "расплывчатые множества". В этой модели производится учет различий между элементами одного класса, и в явной форме признается возможность принадлежности элемента одновременно к двум (и более) классам. Другими словами, четкой границы между классами этой модели не существует. Это изображается с помощью функции принадлежностиM_A(х) объекта х к расплывчатому множеству А, значение которой принадлежит интервалу [0,1]: 0<M_A<1. Например, на Рис.16 изображена расплывчатая классификация чисел на "малые", "средние", и "большие". Сравните ее со старой, "нерасплывчатой" классификацией, изображенной на Рис.16-б, при которой число может принадлежать одновременно ко всем введенным классам, хотя и в разной степени, т.е. с различными значениями функции принадлежности.

Являясь простейшей моделью, классификация лежит в основе всех других, более сложных моделей. Это достигается как увеличением числа классов, так введением вс± новых и новых соотношением между классами.Примерами могут служить: иерархическая классификация УДК; языковые модели (существительные есть имена классов вещей, глаголы - имена классов действий); и т.д., и т.п.

О РЕАЛЬНЫХ МОДЕЛЯХ Разнообразие предметов, используемых в качестве моделей, не позволяет получить содержательных аналитических выводов о реальных моделях вообще. Анализ конкретной реальной модели может быть необходим в конкретных случаях, но выводы будут иметь частный характер. Можно говорить об элементах (деталях) данной модели (например: дактилоскопических отпечатках пальцев), но не об элементе, общем для всех реальных моделей (например: молекулы или атомы - элементы всех реальных объектов, но это не специфично к тому, используются ли эти объекты как модели или нет). Модели являют собой пример систем, познание природы которых возможно лишь пут±м применения синтетического метода.

$3.3 СИНТЕТИЧЕСКИЙ ПОДХОД К ОПИСАНИЮ МОДЕЛЕЙ. В соответствии с синтетическим методом, объяснение природы моделей начинается с указания метасистемы, одним из элементов которой выступает модель. В качестве такой объемлющей системы возьм±м совокупность из четырех составляющих (см. Рис.17):

- субъекта "С", осуществляющего моделирование;

- моделирование объекта "О";

- модели "М";

- культуры, как среды моделирования.

Каждый элемент нашей системы связан с тремя остальными составляющими. Рассмотрение этих связей и позволит вскрыть разные аспекты природы моделей.

ЦЕЛЕВОЙ ХАРАКТЕР МОДЕЛЕЙ в модели отображается не сам оригинал, не все то, что есть в отображаемом оригинале, а только то, что нам нужно, что требуется субъекту для поставленной им цели.

Для разных целей требуется отображать разные стороны объекта, т.е. строить разные модели. Отсюда множественность моделей одного и того же оригинала. Вопрос "Какая из моделей данного объекта лучше?" - некорректен: для одной цели одни модели лучше, для другой _ другие. Модели одного и того же объекта могут даже противоречить друг другу (как корпускулярная и волновая теории света). На статус "единственно верных" претендуют лишь модели религиозного характера. Научные же модели подвергаются постоянному сомнению и проверке на правильность, непрерывно уточняются и развиваются.

Целевой характер моделей позволяет различать модели по типу, характеру целей. Например, полезной классификацией моделей может быть их разделение на познавательные и прагматические, что соответствует целям теоретическим и практическим, получению информации о внешнем мире и процессам его преобразования.

Познавательные модели служат для представления имеющихся знаний и присоединения к ним новых знаний. При обнаружении расхождения между моделью и реальностью изменяет модель, приближая е± к реальности.

Прагматические модели отображают несуществующее, но желаемое (проекты, цели, планы, правовые нормы, программы, алгоритмы, и пр.). При обнаружении отличия между реальностью и моделью мы стараемся изменить реальность, приближая е± к модели.

ИСТИННОСТЬ И АДЕКВАТНОСТЬ Иногда одну и ту же цель можно пытаться достичьс помощью разных моделей. При этом оказывается, что разные модели обеспечивают разную степень успешности в достижении цели. Назовем это свойство модели степенью их адекватности. Если не вводить промежуточных градаций, назов±м модели, используя которые субъект успешно достигает цель, адекватными; а не обеспечивающие достижения цели - неадекватными.

Требование истинности и адекватности могут совпадать (например, для познавательных моделей, т.к. они создаются для правильного отображения реальности), но могут и различаться (часто это относится к прагматическим моделям: к цели может приводить и ложная модель, - ведь иначе ложь вообще была бы не нужна).

ОТНОШЕНИЯ МЕЖДУ ОРИГИНАЛОМ И МОДЕЛЬЮ

I. ИСТИННОЕ И ЛОЖНОЕ В МОДЕЛИ Рассмотрение отношений между оригиналом и моделью в схеме Рис.17 начнем с обсуждения того, в каком соотношении находится информация, заключенная в модели, с моделируемым оригиналом. Смоделируем обсуждаемую ситуацию схемой на Рис.18, где круг М соответствует модели, круг О - оригиналу. Схема высвечивает следующие особенности:

1) Оригинал и модель - это разные вещи. Только сам оригинал является своей абсолютно полной моделью.

2) Модель имеет нечто общее с оригиналом,"истинное" (область I), благодаря которому и может служить его (частичным, специальным) заменителем, представителем.

3) Модель содержит не всю информацию об объекте (область II). Информация, не вошедшая в модель, состоит из тр±х компонент: а)известное, но не существенное для наших целей; б)известное и существенное , но ошибочно включенное в модель; в)неизвестное, и всегда присутствующее, даже если мы сами создали этот объект.

4) У модели всегда есть собственные свойства, не имеющие никакого отношения к оригиналу, т.е. "ложное" содержание.

Это неизбежно даже в том случае, когда мы стараемся включить в модель "только истину": ведь это другой объект, у которого есть присущие только ему, и ничему более, свойства. (Характерный пример - математическое моделирование реальных сигналов.)

ОТНОШЕНИЯ МЕЖДУ ОРИГИНАЛОМ И МОДЕЛЬЮ.

II. ТИПЫ ПОДОБИЯ РЕАЛЬНЫХ МОДЕЛЕЙ. Отвечая на вопрос, как, в результате чего устанавливается похожесть, подобие между моделью и оригиналом, мы можем выделить три типа реальных моделей.

1. Модели прямого подобия. Подобие между моделью и оригиналом устанавливается вследствие непосредственного взаимодействия (след, отпечаток пальца, печать и т.п.), либо вследствие цепочки таких взаимодействий (фотография, макет здания и т.п.).

2. Модели косвенного подобия (аналоги). Подобие между двумя объектами обнаруживается через полное или частичное совпадения их абстрактных моделей. Будучи установленным, таким косвенным подобием может быть использование для моделирования одного из этих объектов другим. Примеры: электромеханическая аналогия, гидропневмоэлектрическая аналогия, аналоговые ЭВМ, исторические параллели, и т.п.). Важным моментом является установление силы аналогии (раздела между областями I и III на схеме Рис.17).

3. Модели условного подобия. В этом случае подобие устанавливается соглашением (персональным или общественным), носит культуральный, условный, информационный характер (символы, знаки, сигналы, деньги, и т.п.). Весьма важный класс моделей условного подобия - знаковые модели. семиотика (наука о знаках) состоит из тр±х разделов, отдельно рассматривающих (см.Рис.17) отношения между знаком и оригиналом - семантика, между знаком и субъектом - прагматика, и между знаком и другими знаками и моделями - синтаксис.

ОТНОШЕНИЯ МЕЖДУ ОРИГИНАЛОМ И МОДЕЛЬЮ.

III. КОНЕЧНОСТЬ И ПРИБЛИЖЕННОСТЬ МОДЕЛИ. Конечность моделей. Удивительно, что конечные модели позволяют эффективно отображать бесконечный мир, но это не так. Модель отражает объект в конечном числе отношений, - определяемом нашими целями. Кроме того, мы (сами являясь конечными) располагаем конечными средствами для моделирования. модель в итоге конечна, хотя реальная модель одновременно есть некий объект, сам по себе бесконечный.

Приближенность моделей. Даже те аспекты оригинала, которые отображаются в модели намеренно, отображаются некоторой точностью, приблизительно. Иногда приблизительность носит вынужденный характер (нехватка знаний), а иногда вводится сознательно, ради упрощения работы с моделью (например, линеаризация).

ОТНОШЕНИЕ МОДЕЛИ И КУЛЬТУРЫ: ИНГЕРЕНТНОСТЬ. Для того, чтобы проявились свойства модели, т.е. чтобы объект

функционировал как модель, - недостаточно только наличия этого объекта. Нужно, чтобы модель была согласована с окружающей средой, которой для модели является культура. Примеры: глас вопиющего в пустыне; книга на незнакомом языке; зашифрованное сообщение; кассета без магнитофона; и т.д.

Ингерентность модели культуре является необходимым условием. Степень ингерентности модели может изменяться: возрастать за счет развития модели (обучение) или за счет изменения среды (история с розеттским камнем), или убывать (тибетские свитки).

ГЛАВА IV. УПРАВЛЕНИЕ

Управлением называется целенаправленное воздействие на систему. Смысл и значение понятия “управление” выходят за рамки системного анализа, а в самом прикладном системном анализе это понятие занимает центральное место. Поэтому важно разобраться в деталях и нюансах этого понятия.

ОБЪЕКТ УПРАВЛЕНИЯ

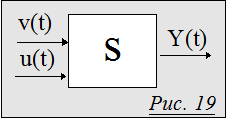Обозначим выходы некоторой реальной системы S символом Y(t), а входы еe разделим на управляемые извне u(t) и не управляемые v(t) (Рис.19). Само выделение управляемых входов означает,что мы рас­сматриваем систему S как объект управления. Выходы Y(t) являются резу­льтатом преобразования системой S входов v(t) и u(t): Y(t)=S(v(t),u(t)), что позволяет воздействовать на Y(t) путем выбора различных управлений u(t).

ЦЕЛЬ УПРАВЛЕНИЯ

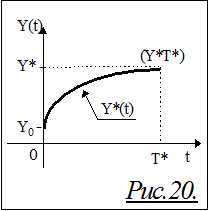
Пусть состояние на выходе системы S в момент времени t=0 есть Y и я, как субъект, этим недоволен. Значит существующая ситуация является для меня проблемной (см.Гл.I), и я хотел бы ее изменить. Желательным уровнем величины Y для меня было бы Y*, пока не существующее в момент t=0. Чтобы повысить уверенность в достижении поставленной субъективной цели (см.Гл.II,п.12), нужно дополнить ее описание соблюдением известных нам объективных и субъективных условий и ограничений. Например: если известно, что Y(t) физически не в состоянии меняться очень быстро, я назначаю ближайший реальный (по моему мнению) срок T* достижения величины Y* (см.Рис.20); теперь точка (Y*,T*) является моей конечной целью. Но прибыть в эту точку можно по разным траекториям, и эти траектории могут быть для меня не одинаково оцениваемыми.

Учитывая теперь остальные известные мне ограничения и требования, я выбираю наилучшую (в смысле критериев, выражающих эти требования и огра­ничения) траекторию Y*(t). Теперь Y*(t) является полным описанием нашей цели.

Подчеркнем два момента. Первый состоит в том, что, хотя мы и постарались учесть все ограничения при формулировке цели, она остается субъективной: во-первых, мы учли только то, что нам известно, а наши знания всегда ограничены; во-вторых, то, как именно и насколько правильно мы это сделали - итог нашей работы, неизбежно несущей отпечаток нашей личности. Так что вопрос о фактической достижимости поставленной цели системой S остается открытым.

Второй момент - предлагаемое определение цели является соби­рательным: оно объединяет все аспекты желаемого будущего. Всякую деятельность (в том числе управление), приведшую к реализации цели, мы называем эффективной. Интересно, что в английском языке имеется терминологическое различие между УСПЕШНОСТЬЮ достижения конечной цели (Y*,T*) (EFFECTIVENESS), и УС ПЕШНОСТЬЮ движения к ней по оптимальной траектории Y*(t) (EFFICIENCY). Оба слова на русский язык переводятся одним, огрубленным словом "эффективность".

Итак, далее функцию Y*(t), вместе с ее концом (Y*, t=T*), но без точки (Y₀ , t=0), будем называть просто целью.

УПРАВЛЯЮЩЕЕ ВОЗДЕЙСТВИЕ

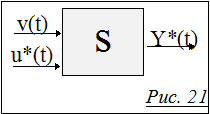Тот факт,что входы и выходы систе­мы S связаны между собой некоторым соотношением Y(t)=S(v(t),u(t)), позволяет надеяться на то, что существует такое управляющее воздействие u*(t), при котором на выходе реализуется цель Y*(t) (см.Рис.21). Но как узнать, действительно ли оно существует, и если да, то каково оно? Из-за потерь при неправильном воздействии обыч­но неразумно, часто недопустимо, а иногда - невозможно перебирать все возможные {u(t)} прямо на входе самой реальной системы в попытках угадать, наконец, u*(t). А что взамен? Заменой самой системе является ее модель.

МОДЕЛЬ СИСТЕМЫ

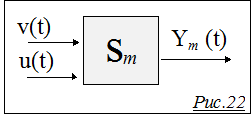Из того, что мы знаем о системе S, мы выделяем сведения, позволяющие построить модель S_m , описывающие связь входов и выходов системы: Y_m = S_m (v(t), u(t)). Подчеркнем, что это не сама система S, а ее описание, модель S_m, наше представление о том, как система преобразует входы в выход (Рис.22). С моделью мы мы можем обращаться более свободно: хотя при подаче на вход модели неудачного управления u(t) мы тоже несем потери (тратим время и другие ресурсы, нужные для работы модели), но эти потери обычно несравнимо меньше тех, которые мы понесли бы, осуществив это неудачное управление на самой системе.* Поэтому на модели мы можем делать то, что очень нежелательно делать в реальности : перебирать любые воздействия в любом порядке, и смотреть, что получится.

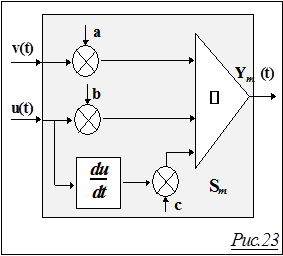Модель может быть абстрактной - на языке любого уровня, от словесного (типа "если <u _i,v >, то <Y _i>, i=1,2,...,N" до математического (типа уравнения Y(t)=av(t)+bu(t)+c 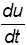, или на неко­тором профессиональном языке (типа блок-схемы на Рис.23). А может быть реальной - в виде некоторого устройства, изобража­ющего действие системы (напри­мер, схему на Рис.23 можно набрать из элементов аналоговых вычислительных устройств). Таким устройством может быть и цифровая ЭВМ, в которую введена программа выполнения всех операций, входящих в уравнение Y_m(t)=S_m(v(t),u(t)).

БЛОК УПРАВЛЕНИЯ

Итак, в акте управления можно уже различить два этапа. Первый - нахождение нужного управляющего воздействия с помощью модели системы. Второй - осуществление найденного воздействия на входе реальной системы. Как мы увидим дальше, для управления иногда могут потребоваться и другие действия, но эти два - обязательно.

Все действия, необходимые для управления, должны быть выпол­нены. Эта функция возлагается обычно на специально создаваемую для этого систему, называемую блоком управления, или системой (подсистемой) управления, или управляющим устройством, и т.п. (см.Рис.24). В реальности блок управления физически может быть подсистемой управляющей системы (как заводоуправление - часть завода, автопилот - часть самолета). Но может воздействовать на систему и извне (как министерство на подчиненное пред­приятие, как аэродромный диспетчер на идущий на посадку самолет). Таким образом, при описа­нии ситуации "объект управления - блок управ­ления" мы сталкиваемся со всеми сложностями построения модели состава, обсужденными ранее в главе II, в виде неоднозначности проведения границы между объектом управления и управляющей системой.

ЭТАП НАХОЖДЕНИЯ НУЖНОГО УПРАВЛЕНИЯ

Рассмотрим принципы работы с моделью S_m для поиска наилучшего управления. Употребив оценочное слово “наилучший”, мы обязаны точно указать, в каком смысле употребляется эта оценка, т.е. задать критерий качества. Ясно, что управление "тем лучше", чем ближе выход системы Y(t) к цели Y*(t). Но искать-то это управление мы будем на модели; поэтому на этапе поиска управления нам придется считать наилучшим то управление u*_m (t), которое максимально приблизит к Y*(t) выход модели Y_m (t). Что значит "Y_m (t) и Y*(t) близки (или далеки)"? Надо ввести критерий близости двух функций, некоторое число r, которое было бы нулем только при Y_m(t)=Y*(t), и возрастало бы при любом их различии. Таких чисел ("расстояний" между двумя функциями) можно ввести много, и по-разному (например,

r₁=max_t (Y_m(t)-Y*(t)), r₂=ò (Ym(t)-Y*(t))Іdt, и т.д.).

Выберем некоторую меру различия двух функций r₁,r₂ в этой записи явно фигурируют входные функции u и v , чтобы подчеркнуть, что разница между Y_m(t) и Y*(t) зависит от того, что есть на входах.

А теперь нам остается решить задачу на отыскание такого u*_m (t), которое доставляет функционалу r минимум (лучше - ноль): ......

******здесь должна быть формула

Пусть эта математическая формула не отпугивает гуманитариев, кото­рые начали изучать данный курс, испытывая аллергию к математике: это всего лишь краткая символическая запись того, что так долго пояснялось "нормальными словами" (хотелось бы, чтобы гуманитарии оценили сжатость математического языка).

ЭТАП ИСПОЛНЕНИЯ УПРАВЛЕНИЯ

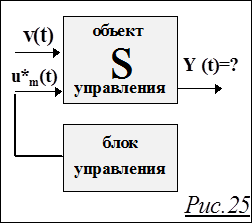
Решив на предыдущем этапе задачу нахождения управления u*_m.(t), мы переходим к этапу осуществления этого воздействия на управляемом входе системы S (см.Рис.25). Самое интригующее - что же получится на выходе системы S? А получиться может что угодно. Рассмотрим два крайних случая.

Простая система.Самый благопри­ятный случай наступает, когда на выходе реальной системы S осуществляется то же, что получалось на выходе модели S_m: Y(t)=Y_m(t)=Y*(t). Это значит, что наша модель является адекватной (по отношению к цели Y*, см.§3.3). Систему S в этом случае будем называть простой, воздействие u*_m.(t) - программой, а данный тип управления - программным управлением.

Программное управление применяется для управления системами, поведение которых в известных обстоятельствах вполне предсказуемо: ЭВМ, телефоны, стрелковое оружие, любые автоматы, идеальное воинское подразделение, образцовый слуга и т.п.

Сложная система.

Другой возможный случай - система S откликается на воздействие u*_m.(t) не так, как модель S_m: Y(t)=S(v(t),u*_m.(t)¹Y*(t). Значит наша модель неадекватна: мы не смогли с ее помощью достичь цели. Система отреагировала не так, как мы ожидали. (Эта чертова штука ведет себя не так, как ей положено!"). Такую систему будем называть сложной. Причиной сложности системы S при таком подходе оказывается неадекватность ее модели S_m.

Это очень существенный момент для всего дальнейшего. Приняв такое определение сложности[1], мы получаем ясное представление о том, как преодолевать сложность. Есть два пути для этого: 1)изменять модель, стараясь повысить ее адекватность, "приближая модель к системе"; 2) вносить изменения в саму систему, пытаясь ее упростить, "приближая ее к модели". Рассмотрим обе возможности в отдельности.

МЕТОД ПРОБ И ОШИБОК

Неадекватность модели означает одно: в модели нехватает информации о системе. И если мы хотим или вынуждены иметь дело именно с данной системой, не изменяя ее саму, то наша задача - добыть эту недостающую информацию. Будем считать, что создавая исходную модель S_m, мы не ограничились только собственными представлени­ями, а использовали все доступные нам знания об S, накопленные в книгах, базах знаний, умах экспертов. Если и при этом система осталась сложной, то единственным источником информации остается только она сама, точнее - эксперимент с нею.

Такое обращение с системой,-экспериментирование над системой в ходе управления ею, -называется методом проб и ошибок. Важно понимать что метод проб и ошибок - единственно возможный метод управления сложной системой. Не менее важно понимать, что это - не метод "тыка", при котором каждое следующее пробное воздействие делается наугад. Метод проб и ошибок ориентирован на минимизацию потерь, к сожалению, неизбежных при совершаемых ошибках. Поэтому очередное пробное воздействие отыскивается опять на модели, но "исправленной и дополненной" с учетом предыдущей ошибки. Так что метод проб и ошибок состоит в циклическом повторении операций <<нахождение на модели № i наилучшего воздействия u*_i.(t) —исполнение u*_m.(t) на реальной системе S a извлечение дополни­тельной информации об S из "пробы - ошибки” a внесение коррекции в модель:S_mi aS_mi+1. a. переход к i +1 шагу.>>

КОРРЕКЦИЯ МОДЕЛИ НА ОСНОВАНИИ ОЧЕРЕДНОГО ЭКСПЕРИМЕНТА.

Конкретизируем, как именно производится коррекция модели по результатам последней ошибочной пробы. Старая модель давала прогноз: если на входе v(t) и u*_m1.(t), то на выходе должно быть Y*(t). Реальная же система ответила: если на входе v(t) и u*_m1.(t), то на выходе Y₁(t) ¹Y*(t). Следовательно, мы должны поправить модель, причем так, чтобы новый вариант модели давал отклик Y₁(t) на входные воздействия v(t) и u₁*(t).

В некоторых случаях такая коррекция делается просто: если модель представлена списком соотношений “если <…>, то <…>”, то поправка сводится к замене одной строки на другую. Но если модель имеет другую форму, то ее исправление лишь отчасти может быть выполнено формально, и в значительной мере является объектом изобретательства, искусства. Проиллюстрируем эти два вартанта примерами.

Первый пример. Вы забыли код, набранный вами на дверце автоматической камеры хранения. Система стала для вас сложной. Приходится пользоваться методом проб и ошибок. Модель имеющаяся у вас, имеет вид: “если набрать код i, то дверь, возможно, откроется (i=1,2,...N, N-число всех комбинаций). При каком-то коде она откроется обязательно”. Вы выбираете способ перебора кодов, который вам нравится больше других (случайный; по порядку номеров; сначала все нечетные; сначала все простые; и т.д.) и начинаете с первого кода. Если дверь открылась, вы превратили систему вновь в простую. Коррекция модели: в первой строке заменяете слова "возможно, откроется" на "откроется", а в остальных - на "не откроется". Если нет - вы в первой строке заменяете слова "возможно, откроется" на "не открывается". Неопределенность уменьшается, но не исчезает, и система остается сложной. Далее - последующая итерация.

Второй пример. Ваша модель S_m1. имеет вид уравнения, например типа

Y*_1m(t)=av(t)+ .

После первой пробы на S имеем:

Y₁(t)=av(t)........ .

Нам надо так откорректировать модель. чтобы она на входы v(t),u*₁(t) тоже давала Y₁(t). Тут-то и пояляется возможность попро­бовать формальный путь: варьировать коэффициенты a,b и с. Если это не приведет к успеху, придется прибегнуть к творчеству: варьировать степени переменных, вводить новые члены, стараясь решить задачу. Но и добившись этого, мы не до конца уверены, что теперь SºS_m. , т.к. их совпадение достигнуто только на данной комбинации входов и выходов. Далее - следующая итерация: метод проб и ошибок предписывает повторять циклы один за другим в стремлении к уменьшению сложности.

Становится ясно, что сложность системы может иметь разную степень выраженности. Практика показывает, что многие сложные системы методом проб и ошибок могут быть превращены в простые иногда за несколько шагов (например, управлять автомобилем), часто потребуется значительное, но конечное число итераций (например, разработать улучшающее вмешательство в проблемную ситуацию, вырастить квалифицированного специалиста). Но есть и системы сложность которых столь велика, что человечество не смогло преодолеть ее за все время своего существования, и можно думать, что они остануться сложными и в будущем (мозг; само человеческое общество; его частные проявления, такие, как экономика, отношения власти; вселенная). Можно принять предложение отцов кибернетики последние системы называть очень сложными, но важно подчеркнуть, что даже при очевидной бесконечности процесса преодоления их сложности, прогресс все же возможен, и именно методом проб и ошибок, хотя ясно, что не на пути постановки конечной цели, а на пути преодоления конкретных препятствий,определения конкретных ограничений, в рамках которых остается свобода для проб и ошибок,

И последнее замечание. Для снижения неизбежных потерь при управлении методом проб и ошибок имеются всего две возможности. Первая - не повторять ошибок, совершенных в прошлом (запрет на уже использованные воздействия). Вторая - ликвидация потерь полезной информации в ходе ее преобразования из формы {u*_i.(t),Y_i.(t)} в форму S_mi aS_m(i+1). Поэтому так важно совершенствование методов извлечения как можно большей доли полезной информации из результатов опыта. Этим занимаются многие дисциплины: анализ данных, математическая статистика, теория информации, теория моделирования, планирование экспериментов, анализ сцен и распознавание образов, искуссвенный интеллект, и т.д.

Итак программное управление и метод проб и ошибок исчерпывают наши возможности управления, если мы воздействуем на систему, не изменяя ее, а опираясь только на результаты ее модели­рования.

Обратимся теперь к возможностям управления, которые открыва­ются, если мы можем что-то изменять в самой системе. Таких возмож­ностей две.

РЕГУЛИРОВАНИЕ

Первая - изменять некоторые параметры (внутренние перемен­ные) системы. Этот тип управления иногда называют управлением по параметрам. Оно позволяет преодолевать сложность системы, при которой она "не слишком" отличается от простой. Поясним, что это значит.

Пусть на основе модели . S_m рассчитана целевая траектория системы Y*(t) (в этом случае она называется "опорной"). Реализуя соответст­вующую программу u*(t), мы запускаем систему по опорной траектории (летчик получает полетное задание, шофер - маршрут следования и график движения по нему, следящее устройство - уставку, и т.п.). Но скоро выясняется, что реальность несколько сложнее (летчику мешает ветер, шоферу - непредвиденные задержки и объезды, станок сбивается с уставки), и система "сходит" с опорной траектории. Но не слишком далеко, и не слишком быстро - так, что остается возможность вернуть ее на опорную траекторию: это целесообразно, поскольку это приведет нас к цели, хотя и "приблизительно" (см.Рис.26). Управление путем приблизительного удержания системы на целевой траектории за счет изменения некоторых параметров системы называется регулированием. Для осуществления регулирования нужно устройство (называемое регулятором), выполняющее новые функции, которых не требовалось при программном управлении:

1)держать в памяти опорную траекторию Y*(t);

2)следить за реальной траекторией Y(t) , поскольку она может отличаться от Y*(t);

3)обнаруживать текущее различие между Y*(t) и Y(t) (причем в разных ситуациях может потребоватся следить за разными характеристиками их различия: просто разницей; квадратом разности; разницей производных какого-то порядка; других мер различия).

4)вырабатывать корректирующее, дополнительное к u*(t) воз­действие на параметры системы, подавая его на исполнительное устройство, осуществляя отрицательную обратную связь (так называется связь от выхода (Y(t)) ко входу (u(t)), уменьшая разницу между Y и Y*). Поэтому говорят о программном управлении как об управлении без обратной связи, а о регулировании - как об управлении с отрицательной обратной связью.