Решение задачи симплексным методом

Суть этого метода состоит в переходе от одного опорного решения к другому при условии, что значение целевой функции при этом будет увеличиваться.

Рассмотрим решение предыдущей задачи:

12x₁ + 4х₂ ≤ 300,

4х₁ + 4х₂ ≤ 120,

3х₁ + 12х₂ ≤ 252,

x₁, х₂ ≥ 0.

F = 30x₁ + 40х₂ → max

Перейдем к основной задаче линейного программирования путем введения дополнительных переменных x₃, х₄, x₅, которые по физическому смыслу означают неиспользованный ресурс времени плиточников, штукатуров и маляров то есть от системы ограничений вида неравенств перейдем к системе ограничений вида равенств.

12x₁ + 4х₂ + х₃ = 300,

4х₁ + 4х₂ + х₄ = 120,

3х₁ + 12х₂ + х₅ = 252,

x₁, х₂, x₃, х₄, x₅ ≥ 0.

F = 30∙x₁ + 40∙х₂ + 0∙х₃ + 0∙х₄ + 0∙х₅ → max

Запишем систему ограничений в векторной форме:

,

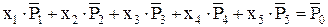где векторы: ; ; ; ; ; .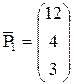

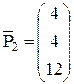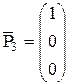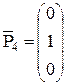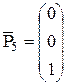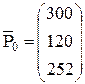Среди системы векторов 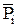есть три единичных вектора 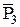, , 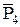, 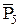которые образуют базис. Задача имеет невырожденный опорный план X₀ (0, 0, 300, 120, 252) и ее можно решить табличным симплекс-методом. Составим симплекс-таблицы:

№ табл.	i	базис	Cб	Р0						Θ	Примечание
Р1	Р2	Р3	Р4	Р5
I		P3								300/4=75	т. О (рис. 1.1)
	P4								120/4=30
	P5								252/12=21
	∆j = zj – сj		-30	-40
II		P3							-1/3	19,64	т. A (рис. 1.1)
	P4							-1/3
	P2			1/4				1/12
	∆j = zj – сj		-20				10/3
III		P3						-11/3	8/9		т. B (рис. 1.1)
	P1						1/3	-1/9
	P2						-1/12	1/9
	∆j = zj – сj					20/3	10/9

Поясним заполнение симплекс-таблиц.

Таблица I. В 4-ой строке в столбце P₀ записываем скалярное произведение 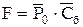= 300 ∙ 0 + 120 ∙ 0 + 252 ∙ 0 = 0. Таким образом, прибыль по опорному плану составляет 0 у.е. В остальных столбцах этой строки записываем 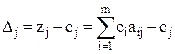, j = 1,… n. ∆₁ = 0 ∙ 12 + 0 ∙ 4 + 0 ∙ 3 – 30 = –30, ∆₂ = 0 ∙ 4 + 0 ∙ 4 + 0 ∙ 12 – 40 = –40 и т.д.

Определяем вектор для ввода в базис из векторов, для которых ∆_j < 0 (4-ая строка). Возьмем вектор Р₂, так как он соответствует наименьшему ∆_j = ∆₂ = –40. Столбец, соответствующий вектору Р₂ является направляющим.

Вектор для вывода из базиса определяем по числу 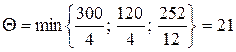. Это значение соответствует вектору Р₅. Эта строка является направляющей. Элемент a₂₃ = 12 является разрешающим элементом. Заполнение таблицы II начинается с заполнения направляющей строки делением всех ее элементов на a₂₃ = 12. Остальные элементы таблицы II вычисляются по формуле Жордана-Гаусса.

Например, 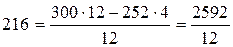, 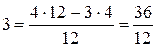и т.д.

В таблице II в 4-ой строке, есть отрицательное число ∆_j. Оно соответствует вектору Р₂. 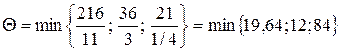соответствует базисному вектору Р₃. Таким образом, вектор Р₃ выводим из базиса, а вектор Р₂ вводим в базис Элемент a₁₂ = 3 является разрешающим. Прибыль по этому плану составляет 840 у.е

Перерасчет элементов таблицы III осуществляется как и раньше. В таблице III в 4-ой строке среди ∆_j нет отрицательных, следовательно, получен оптимальный план: X_опт (12, 18, 84, 0, 0), F_max = 1080 у.е.

Покажем соответствие опорных решений и вершин области допустимых решений (ОДР). Опорное решение X₀ (0, 0, 300, 120, 252) соответствует точке О (0; 0) ОДР. Решение X₁ (0, 21, 216, 36, 0) соответствует точке А (0; 21). Оптимальное решение X₂ (12, 18, 84, 0, 0) соответствует точке B (12; 18) ОДР.