Них являлась функцией другой?

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Методические указания для студентов заочной

Формы обучения

Составители Л.И. Лесняк,

М.В. Зголич

Томск 2008

Введение в математический анализ: методические указания / Сост. Л.И. Лесняк, М.В. Зголич. – Томск: Изд-во Том. гос. архит.-строит. ун-та, 2008. – 76 с.

Рецензент профессор Н.Н. Белов

Редактор Е.Ю. Глотова

Методические указания предназначены для студентов первого курса общеобразовательного факультета ТГАСУ заочной формы обучения. Рекомендуется использовать при изучении раздела «Введение в математический анализ» и выполнении контрольной работы № 3. Указания содержат введение, краткие теоретические сведения, необходимые для решения задач, методические рекомендации по решению типовых задач, варианты контрольных заданий и список рекомендуемой литературы. Методические указания могут быть использованы студентами первого курса очной и дистанционной форм обучения.

Печатаются по решению методического семинара кафедры высшей математики, протокол № 2 от 20 ноября 2007 г.

Утверждены и введены в действие проректором по учебной работе В.В. Дзюбо

с 01.09.2008

до 01.09.2013

Подписано в печать.

Формат 60х90х16. Бумага офсет. Гарнитура Таймс, печать офсет.

Уч.-изд. л. 4. Тираж 250 экз. Заказ №

Изд-во ТГАСУ, 634003, г. Томск, пл. Соляная, 2.

Отпечатано с оригинал-макета в ОПП ТГАСУ.

634003, г. Томск, ул. Партизанская, 15.

ВВЕДЕНИЕ

Все что окружает человека, непрестанно изменяется, и вся практическая деятельность человека направлена на изменение окружающего мира. Изучение характера изменения различных величин, поиск закономерностей, которым эти изменения подчиняются – основная задача аппарата математики, который принято называть математическим анализом. Фундаментом математического анализа является раздел «Введение в математический анализ». Изучению этого раздела и посвящены данные методические указания.

Методические указания составлены так, чтобы помочь студенту, приступающему к изучению высшей математики, организовать свою самостоятельную работу, разобраться в обилии определений и теорем начал математического анализа, выделить и усвоить главное, приобрести прочные навыки решения задач различного уровня сложности.

Содержание указаний разбито на темы:

1. Понятие функции.

2. Понятие предела функции.

3. Понятие непрерывности функции в точке.

4. Техника вычисления пределов.

5. Классификация точек разрыва функции.

Изложение каждой темы содержит:

1. Основные теоретические сведения, которые представлены в виде вопросов и ответов с необходимыми комментариями. Многие из вопросов носят проблемный характер. Предполагается, что свой вариант ответа студент может сравнить с предложенным и сделать соответствующий вывод. Всюду, где это необходимо, теоретический материал иллюстрируется графически, что значительно облегчает усвоение теории.

2. Методические рекомендации по решению типовых задач. Помимо задач вычислительного характера рассмотрены задачи на качественное усвоение теории. Сложность рассмотренных в каждой теме задач повышается постепенно. Задачи предлагаются в количестве, достаточном для приобретения навыка решения каждого из заданий, являющихся для студентов заочной формы обучения содержанием контрольной работы № 3.

Условия задач и таблица с номерами контрольных заданий для каждого варианта приведены в конце пособия. Напомним, что студент должен выполнить контрольное задание по варианту, номер которого совпадает с последней цифрой его учебного шифра.

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

ПОНЯТИЕ ФУНКЦИИ

1.1. В связи с чем возникло понятие функции?

Изучение любого процесса происходит путем изучения характера изменения переменных величин, участвующих в этом процессе. При этом, как правило, характер изменения одних величин зависит от характера изменения других. Понятие функции возникло в связи с необходимостью каким-то образом описать эту зависимость.

Каким должен быть характер изменения

Двух переменных величин, чтобы одна из

них являлась функцией другой?

Функция считается заданной, если задан закон, по которому каждому значению переменной x из некоторого множества X ставится в соответствие единственное значение переменной у из множества Y, в котором эта переменная принимает свои значения.

Для функциональной зависимости приняты обозначения: y = f(x), y = φ(x), y = F(x) и т. п. Множество Х называется областью определения функции, переменная x независимой переменной или аргументом, множество {f(x)} называют областью значений функции y = f(x) (очевидно {f(x)} 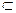Y ).

Часто в качестве синонима слова «функция» используется термин «отображение», при этом говорят, что задано отображение множества X во множества Y и используют обозначение: 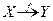. Есл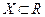и и 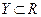, то функция y = f(x) называется вещественнозначной функцией вещественной переменной.

Роль аргумента может играть время, длина дуги, угол и другие переменные величины.

Пример.Материальная точка падает в пустоте под
действием силы тяжести с высоты h.Обозначим через y высоту точки в момент времени t, протекшего от начала движения.
Очевидно, что значение переменной y будет зависеть от значений t, и, следовательно, y является функцией аргумента t. Из курса физики известно, что зависимость y от t выражается формулой

.

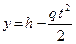В момент падения y = 0 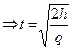. Это означает, что аргумент t принимает свои значения на промежутке 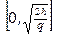, который является областью определения функции. При этом 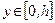,то есть промежуток 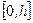– множество значений функции .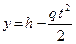