Методика выполнения задания 3
Для решения системы уравнений создадим два М-файла – файл-функцию для решения системы уравнений методом Крамера и файл-сценарий, где будут определяться исходные матрицы и вычисляться вектор корней системы.
3.1. Создайте файл-функцию. Для этого М-файла на панели инструментов нажмите Новый М-файл (New M-file), либо выполните команды File – New–M-file.
Открывается окно М-файла. Сюда введите операторы, соответствующие решению системы уравнений методом Крамера. Назовите функцию Kramer. Входными аргументами являются матрица системы А и вектор свободных членов b, выходными – вектор Х. Название функции, набор входных и выходных параметров определяются первым оператором файла-функции, имеющим следующий вид: function X = Kramer (A, b)
Далее рассчитывается определитель матрицы системы А, вводятся новые матрицы А1, А2, А3 и А4, где соответственно 1-й, 2-й, 3-й и 4-й столбцы заменяются столбцом свободных членов b, рассчитываются определители новых матриц и элементы вектора корней системы Х. Файл-функция имеет вид, представленный на рисунке 1.3. Вектор Х представляет собой вектор-столбец. На это указывает нумерация элементов вектора, где первая цифра номер строки, вторая – номер столбца. Если пронумеровать элементы вектора Х, как Х(1), Х(2), Х(3) и Х(4), то вектор Х будет представлять вектор-строку.
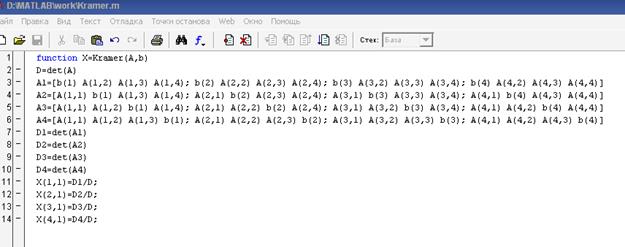
Рисунок 1.3 – Файл-функция решения системы уравнений методом Крамера
3.2. Сохраните файл-функцию под именем Kramer в папке work каталога MATLAB. Обязательное требование – имя файла должно совпадать с именем функции (Kramer).Для этого выберите в строке меню Файл (File) – Сохранить как (Save As), или на Панели инструментов нажмите Сохранить(рисунок 1.4).
Рисунок 1.4 – Сохранение М-файла
3.3. Создайте файл-сценарий, где будут указаны исходные матрицы, произведен вызов созданного ранее файла-функции Kramer и решена система уравнений матричным методом.
Аналогично пункту 3.1 создайте новый М-файл. Запишите в него следующий программный код
% Решение системы уравнений
A=[1 1 1 0; 1 -1 3 1; -1 2 0 3; 3 1 1 -1]
b=[3; 7; -2; 7]
% Решение методом Крамера
Xk=Kramer(A,b)
% Решение матричным методом
Xm=inv(A)*b
3.4. Запустите на выполнение файл-сценарий. Для этого в строке меню выберите Отладка (Debug) – Сохранить и запустить (Save and Run).Следует помнить, что на решение запускается именно файл-сценарий, а не файл-функция. Происходит выполнение программы.
В Окне команд отображаются результаты выполнения каждой строки программы, где в конце строки нетзнака «точка с запятой (;)». Это удобно при отладке программ. Если вы не хотите вывода промежуточных результатов, то в конце соответствующей строки программы поставьте знак «точка с запятой». Ошибки отображаются в Окне команд красным цветом.
3.5. Проанализируйте результаты расчетов. В Рабочей области (Workspace) окна MATLAB отображаются переменные и массивы, введенные в программу и рассчитанные в ней (рисунок 1.5).
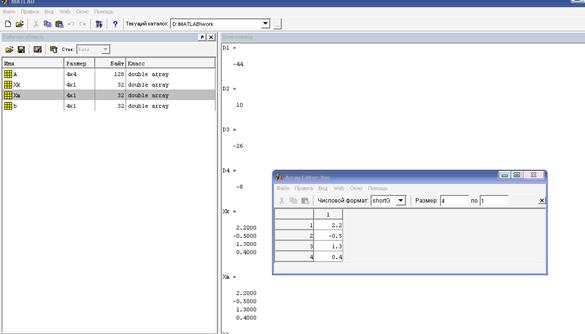
Рисунок 1.5 – Результаты решения задачи
В данном случае будут отображаться матрица А, вектор-столбец b, векторы-столбцы результатов решения системы, методом Крамера – Xk, матричным методом Xm. Щелкнув дважды левой кнопкой мыши по любому массиву или переменной из Рабочей области, можно раскрыть их значения в специальном окне Array Editor.
3.6.Завершите работу MATLAB.
