Представляет собой неопределенное выражение?

Только в одном случае – когда одна из функций является бесконечно малой при 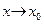, другая бесконечно большой. В этом случае при 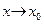произведение 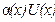называют неопределенным выражением вида (0∙∞).

Например, произведение x lg x является при 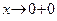неопределенным выражением (0∙∞).

4.7. Что можно сказать о 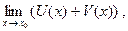если U(x)иV(x)– бесконечно большие приx → x₀?

Если U(x)и V(x) бесконечно большие одного знака, то их сумма тоже будет бесконечно большей величиной того же знака.

Если же U(x) и V(x) являются бесконечно большими при x → x₀ разных знаков, тогда их сумма представляет собой неопределенное выражение вида (∞ – ∞). Например, 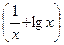– неопределенное выражение вида (∞ – ∞) при x→0+0; выражение 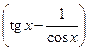является неопределенным выражением вида (∞ – ∞) при .

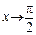Как найти предел степенно-показательной

Функции?

Степенно-показательной называется функция вида

,

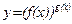функция определена при условии f(x)>0, f(x)≠1. Функция g(x) может принимать любые значения. Чтобы иметь право такую функцию отнести к элементарным, ее принято записывать в виде

.

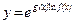Таким образом,

.

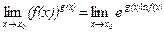В случае, когда функции f(x) и g(x) непрерывны в точке x₀, будем иметь:

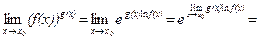
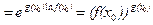при условии, что f(x)>0 .

Например, .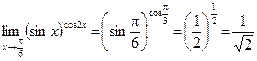

4.9. В каких случаях 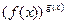будет при x →x₀

Неопределенным выражением?

При вычислении пределов степенно-показательных функций могут встретиться неопределенные выражения трех видов: (0⁰); (∞⁰); (1^∞).

Например,

x ^x – неопределенное выражение вида (0⁰) при x →0+0;

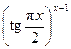– неопределенное выражение вида (∞⁰) при x→1–0;

(cos x)^1/x – неопределенное выражение вида (1^∞), при x →0.

На основании всего вышеизложенного перечислить все возможные неопределенные выражения

Пусть , , , ,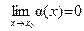

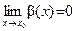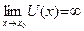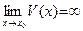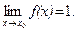
Тогда неопределенными при x →x₀ будут выражения:

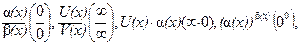
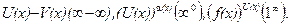
Заметим, что все вышеизложенное имеет место и при x → ∞. Поэтому, в частности, приведенные теоремы можно использовать и при нахождении предела числовой последовательности.

ПРИМЕРЫ НА ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ

ФУНКЦИИ

На основании изложенного выше рекомендуется следующий порядок нахождения предела функции:

1. Если заданная функция непрерывна в точке x₀, нахождение предела сводится к вычислению значения функции в точке x₀.

2. Если при подстановке значения x₀в выражение функции оказалось, что имеет место одна из ситуаций, которые рассмотрены в п.4.3, 4.5 и 4.6, нужно воспользоваться соответствующими теоремами о пределах и свойствами бесконечно малых и бесконечно больших величин.

3. Если оказалось, что при x →x₀ имеет место неопределенное выражение (п. 4.4, 4.6, 4.7, 4.9), следует, установив вид неопределенности, найти специальный прием, позволяющий, как принято говорить, раскрыть данное неопределенное выражение. Специальные приемы раскрытия неопределенностей будут рассмотрены при решении задач.