Динамические переходные процессы на решётке вакуума
Мы живём на решётке вакуума?
Второе издание книги «Мы живём на экране сверхдисплея?
(2007, ISBN 978-5-900891-74-7)
А точнее обратный перевод с английского книги:
“Are we living in the lattice-vacuum?” (2011)
Содержание
Предисловие
От «вакуума» Дирака к «калибровочным полям» Янга-Миллса ……………… 2
Глава Первая
В каком собственно «пространстве» мы живём?
Поль Дирак и его «непустой вакуум» …………………………………………………………… 4
Константа дискретности энергии Макса Планка (h) …………………………………… 5
Попытаемся определить верхнюю границу размера планкеонов ….………… 6
Сеточно-калибровочные поля как «решётка кристалла» в ТТТ ………………… 9
Рис.1. Деформационное поле планкеонов с дефектом в центре ……………… 10
Рис.2. Гравитационное взаимодействие двух дефектов …………………………… 13
Объяснение равенства гравитационной и инертной масс ………………………… 13
Равномерное движение становится “квантовыми скачками” дефектов …… 13
Глава Вторая
Переходные динамические процессы на решётке пространства ……………… 15
Локальная гравитационная волна ……………………………………………………………… 15
Рис.3. Реакция поля планкеонов на скачок дефекта ………………………………… 16
Рис.4. Поле «дефекта» проходит через две щели …………………………………… 18
Фотон как часть электрон-протонного “торнадо” магнитной «жидкости» 19
Глава Третья
Электро-магнитные эффекты в кристаллическом вакууме
Кирхгофф приравнял «ток смещения» к “магнитной жидкости” …………… 20
Попробуем “перевернуть” физическую модель Максвелла …………………… 21
Рис.5. Вакансии электрона и протона с “магнитной жидкостью” …………… 22
Гипотезы о природе Кулоновских сил взаимодействия дефектов ……………23
Первое уравнение Максвелла в "магнитной среде" с дефектами …………….24
Попытки физической интерпретации других уравнений Максвелла ……… 25
Глава Четвёртая
Что сэр Ньютон подразумевал под своими “бесконечно малыми”? ………… 28
Откуда берётся инерция в любой "материальной точке"
Что делать математикам когда они достигают структурных границ?
Физический смысл “роторов” в третьем уравнении Максвелла ………………… 34
Физический смысл E и B компонент магнитной среды ………………..…………… 35
Глава Пятая
Время как мера изменений …………………………………………………………………………… 36
“Принцип наименьшего действия” и другие свойства любых систем ……… 40
Глава Шестая
Иерархия философский определений в контекста понятия “время” ………. 42
Глава Седьмая
Применение локальной меры изменений вместо “времени (t)” ………………… 47
--- <> ---
Предисловие
В этой книге автор пытается предугадать последствия принятия гипотезы «сеточного пространства» («дискретной решётки вакуума»). Подозрение что вакуум это “не совсем ничто” пожалуй впервые «разрешили высказать» только Полю Дираку (примерно в 1930). Позже сам термин (решётчатое пространство) был предложен Янгом и Миллсом (С. Yang and R.Mills) в 1954, когда они пытались объяснить “сильное взаимодействие”. Рождённая в итоге Квантовая Хромодинамика особо не нуждалась в «наглядной интерпретации» и калибровочное сетчатое пространство быстренько замели под ковёр, как ненужный строительный хлам…
Позже было предложено достаточно много вариантов “калибровочных (gauge) дискретных полей“, но только Янг и Миллс удостоились Нобелевской Премии (будем считать что именно за это (:0)).
Большинство типов “калибровочных полей” считались безмассовыми и обычные частицы в них приобретали массу методом нарушения локальной симмметрии этого поля при ускоренном движении…
В этой книге мы попытаемся оценить идею объединения калибровочных и обычных частиц в некое единое «сеточно-кристаллическое» вакуумное поле. Автор даже пытался построить функционирующие компьютерные модели такой решётки пространства с дефектами – и некоторые картинки с экрана функционирующих моделей представлены в книге.
Смысл идеи в том, что в такой объединённой «калибровочной решётке» её узлы при некоторых условиях становятся частицами (в обычном смысле). Но «равномерное движение» частиц при этом приходится заменять на «скачки дефектов» - от одного узла решётки к другому ближайшему…
Подробности новой модели читайте в первой главе книги.
Одним из главных требований теории Янга-Миллса была «калибровочная инвариантность» описания поведения ядерных частиц при движении в сеточно-калибровочном поле, что было возможно только если калибровочные поля были безмассовыми. В те годы (1954) вряд-ли кому-то из физиков приснилось бы в страшном сне, что частицы могут быть одновременно безмассовыми и неподвижными…
У автора есть надежда, что в наше время такого рода «экзотика» уже никого не пугает (?) (:0).
Последствиями принятия такой модели могло быть:
-достаточно убедительное объяснение всех гравитационных эффектов, включая равенство тяжёлой и инертной масс;
-наглядная физическая интерпретация Римановской геометрии с дополнительными «измерениями» - дискретными полями с дополнительными физическими параметрами.
Проще говоря, «кривизна в 4-м измерении» Риманового пространства – с точки зрения физики может описываться тензором деформации нашей «решётки пространства».
Одна из глав книги посвящена попыткам корректной физической интерпретации Ньютоновских «бесконечно малых частиц». Должны ли мы вслед за Ньютоном считать их «безразмерными материальными частицами»? Или всё-таки Макс Планк был прав и «масштабирование» физических процессов нужно останавливать при достижении некоторых качественных структурных границ рассматриваемых систем?
В этом свете, можем ли мы считать «континнуальную» метрику Минковского хорошим основанием для физических моделей на ВСЕХ структурных уровнях?
Однако математики очень давно изобрели замечательный трюк – во всех случаях когда моделируемой «континнуальной» системе необходимо добавить некую «степень свободы» (для выхода за её структурные границы) – они применяют «мнимые числа»…
Автор пытался понять – есть-ли какой-то физический смысл в таком переходе в «комплексные пространства»? И к удивлению обнаружил, что такой переход в большинстве случаев «спасает» континнуальную парадигму безразмерного поля точек и позволяет получить физически корректный результат из физически неверных предпосылок (:0). Просто потому что в результате наложения «калибровочных мнимых полей» итоговая система получает некоторые дополнительные «степени свободы» - в основном за счёт чисто мнимых частей переменных, которые имитируют некие дополнительные «частоты» - и таким образом система получает некоторый вариант «преобразования по Лапласу»…
Да, переход к мнимым переменным это трюк – но вот прямо сейчас автор не готов предложить для него физически корректную альтернативу. Ну разьве-что компьютерные модели в логике клеточных автоматов…
Последняя глава книги посвящена попыткам корректной физической интерпретации понятия «время».
Автор обнаружил давно забытую идею Тита Лукреция Кара (55 год до н.э., Древний Рим) – что никакого «времени самого по себе» не существует. Время это только мера локальных изменений. Тут нет каких-то особых отличий от времени Минковского-Эйнштейна. Хотя… читайте…
По поводу стиля изложения в книге – и как следствие её целевой аудитории. Автор не «перегружал» книгу формулами. Если честно – их там почти совсем нет (:0). Ну мне же не удалось найти соответствующую группу Ли для описания всех своих идей – так чего уж… (:0). Да и вряд-ли детальный разбор особенностей уравнений Янга-Миллса будет интересен более чем 10 физикам…
Поэтому я приглашаю к обсуждению идей, высказанных в этой книге, ВСЕХ кто считает что ему «есть что сказать» по этому поводу…
Пишите мне:
Картинки в тексте это «срезы» моделей автора. Модели выполнены в логике «клеточных автоматов», но не с помощью Вольфрамовской «Математики», а по моей собственной моделирующей программе (:0).
ГЛАВА ПЕРВАЯ
"В каком собственно пространстве мы живём?"
Многие известные учёные «натыкались» на идею, что наше пространство может быть какой-нибудь «решёткой».
Хочу сразу предупредить, что в этой книге мы НЕ БУДЕМ обсуждать идею «газо-подобного» пространства («эфира»).
В начале 20-го века было очень убедительно доказано, что такого рода идеи совершенно несостоятельны. Для меня наиболее убедительным был аргумент, что в газо-подобных полях нельзя установить недиссипативных статических взаимодействий на сколько-нибудь значительных расстояниях. Если даже предположить, что гравитация имеет «обменный характер», то и в этом случае в газо-подобных средах она не сможет поддерживаться из-за диссипации на частицах среды – особенно на расстояниях в световые годы…
Ну собственно поэтому физики тех времён так единодушно перешли к «абсолютно пустому» вакууму – чтобы он не мешал летать их «обменным частицам» (:0).
К идее что «вакуум» может и не быть «абсолютной пустотой» в 20-м веке пожалуй первым пришёл Поль Дирак. Точнее он был первым из тех кто обладал достаточным авторитетом, чтобы высказать эту идею и не пойти после этого работать дворником…
К тому же к этому моменту у него уже была репутация «эксцентричного» учёного и «нашего шалуна» как-то простили…
Его «квантовое поле» (в работе 1927 года) уже не содержало «просто частиц» - частицы уже были «возбуждёнными состояниями» квантового поля.
Известное уравнение Дирака для электрона движущегося в квантовом поле (1928) допускало решения с «отрицательными энергиями». Поначалу эти решения просто отбрасывались как «физически бессмысленные» (счастливое было время – кто-то ещё вспоминал про смысл (:0)). Но позднее Дирак предположил, что электроны с отрицательной энергией «где-то» существуют. И к всеобщему удивлению через пару лет были открыты «позитроны» (1932).
Оставалось только объяснить откуда они берутся.
Ага, значит (все?) частицы это всего-лишь состояния… чего? Вакуума?
Одним из следствий уравнения Дирака была возможность для электрона излучить фотон и перейти в состояние с отрицательной энергией. Для того чтобы исключить такой переход Дирак вынужден был предположить что «вакуум» состоит из «ячеек» уже заполненных электронами с отрицательной энергией. То есть обычно электрон не имеет возможности так плохо поступить. Но в некоторых специальных случаях он всё-же может «выбить» позитрон и встать на его место. То есть потенциально возможно существование и «незаполненных» слотов…
Но дальше этого у Дирака дело не пошло.
Кто-то из физиков более позднего времени доказал, что «квантовое поле» Дирака рассматривало только электрическую составляющую всех возможных взаимодействий частиц – а значит и не могло дать корректного описания очень многих процессов. По этому поводу было забыто и само исходное предположение Дирака о «непустом вакууме со слотами».
Ну ладно, придётся разбираться самостоятельно (:0).
Предположим, что наше «пространство» («вакуум») состоит из дискретных «слотов», то есть наше пространство НЕ континнуальное а «сетчатое».
И давайте для простоты называть эти узлы сети «планкеонами».
Разумеется планкеон это НЕ ещё одна из множества «обменных частиц» - это что-то гораздо более фундаментальное. Почти как Z-бозон (шучу!).
Макс Планк (в 1900) доказал, что все процессы подчиняющиеся законам Термодинамики, НЕ должны описываться «континнуальными» уравнениями. Он предложил «полу-эмпирическую» формулу энергетического спектра «чёрного тела», которая базировалась на понятии «кванта энергии» - дискретной порции энергии которая должна быть излучена по принципу «всё или ничего».
Излучаемые порции энергии должны быть кратны постоянной Планка:
h = 6,626 * 10-34 [J*sec]
Размерность постоянной Планка не совсем энергия, а энергия-на-время – то есть работа. Это работа по излучению «кванта» из… из чего?
Можем ли мы использовать полученные Планком результаты термодинамического исследования излучения «чёрного тела» - прямо к «решётке вакуума»? И таким образом попытаться определить размеры «квантовой ячейки» («планкеона»)? Скорее всего не напрямую, потому что это будет зависеть от того что считать «чёрным телом» на этом структурном уровне.
Естественно предположить, что излучение происходит со скоростью света:
c = 299 792 458 [m/sec] ≈ 3*108 [m/sec].
И остаётся прикинуть сколько узлов решётки может участвовать в излучении одного Планковского кванта энергии (что бы он из себя не представлял).
По формуле Планка:
E = h*ω = (h*c) / λ
Где λ это длина волны излучённой энергии.
Этой формулы пока не достаточно для определения размеров узла решётки, потому что формула сама по себе не содержит ограничений на энергию излучённой частицы… Нужны ещё какие-то ограничения на допустимые частоты…
Попробуем ввести дополнительные ограничения из-каких-нибудь «практических» соображений.
Самые жёсткие γ-лучи имеют длину волны около 0,01 [nm] = 0,1 [Å]- и это пока ещё размеры орбиты электрона в атоме.
Энергия таких лучей (гамма-фотонов) оценивается в 124000 [eV] ≈ 0,1 [MeV] – эту величину мы потом используем для преобразований энергии в длину волны.
“Низко-энергетические” ядерные реакции (типа Хиросимы) идут с энергией порядка 10 [MeV] – что даёт нам длину волны порядка 0,1[Å]/100 = 10-3[Å].
“Высоко-энергетические” ядерные реакции (в фазотронах) идут с энергией порядка 1000[MeV] = 1 [GeV], что даёт нам длину волны порядка 10-5[Å].
Последние исследования на Теватроне и БАК (LHC) идут с энергиями порядка 100 [GeV] – и поскольку они всё ещё выдают какие-то новые преобразования частиц – естественно предположить что и это ещё не уровень самой решётки (узлов, планкеонов)…
То есть 10-7[Å] – даже ещё не «верхняя оценка» размеров волн от планкеона.
Давайте для надёжности пересчитаем эту величину другим способом (по размерности электрон-вольта):
1 [eV]=1,6*10-19[J]
1 [MeV] = 1,6*10-13[J]
1 [GeV] = 1,6*10-10[J]
100 [GeV] = 1,6*10-8[J]
λ = (h*c)/E = (6,6*10-34 * 3*108)/ 1,6*10-8[J] =
≈ 10-17 [m] = 10-7[Å]
Хочу напомнить, что пока мы определяли только верхнюю границу длины волны, которую можно было-бы излучить «непосредственно планкеоном» - но между длиной волны и размерами излучателя может быть разница в несколько порядков…
Особенно при такой скорости излучения…
Но мы не можем просто «взять и поделить» (на скорость света). Кстати, в первой книге я именно так и сделал (:0).
Это была бы чисто математическая операция не имеющая особого физического смысла. Как-бы предположить, что в длине волны должно укладываться именно © источников… С чего-бы?
Для сравнения методов, можно было-бы предложить аналогию из газовой акустики, где считается что устойчивая стоячая волна не может образоваться если излучатель не имеет размеров хотя-бы в четверть длины волны. Но это тоже перебор, только в другую сторону – всё-таки у нас кристалл, а не газ…
Средняя из этих аналогий – по длине свободного пробега в жидкостях – даёт разницу между длиной волны и размерами источника аж до 105. Не исключено…
В одной «очень современной» теории про «глюоны» размеры «кварков» оцениваются как «меньше чем» 10-19 [m] = 10-9[Å].
Вот эту цифру скорее всего и можно взять в качестве верхней границы оценки размеров планкеона…
--- <> ---
Ну ладно, а после Дирака всё-таки кто-нибудь высказывал предположения что «вакуум» не совсем пустой?
Просматривая некоторые работы, которые могли бы близко подойти к такой идее, я нашёл статьи Карло Ровелли по «Замкнутой Квантовой Гравитации» (LQG).
Он «немножко критикует» Квантовую Теорию Поля (QFT) за то что в ней квантово-механические процессы происходят «на фоне» квантового поля (то есть отдельно от него - не совсем так как было у Дирака). И в то же время частицам в QFT разрешено самостоятельно порождать какие-то «структуры» в квантовом поле. Он определяет такое состояние QFT как «нездоровый дуализм», который приводит к противоречиям QFT и Общей Теории Относительности (GR).
Ровелли предлагает рассматривать «компоненты пространства-времени» в QFT как результат квантовых операций над QFT-частицами – то есть процессы в частицах будут как-бы «порождать пространство-время». И это, по его мнению, может привести к счастливому объединению QFT и GR.
Основной целью своей новой теории (LQG) он объявляет «QFT без статического фона пространства-времени» (вот интересно как-бы к этому отнёсся Энштейн, услышав что его теория теперь «вторична»). Теперь всё это является уже следствием квантовых процессов (с частицами) – они «поднимают» квантовую волну в квантовом поле (?) и эта волна состоит из (не очень мне понятных) «круговых нормировок» (loop gauges) - «круговых состояний» квантового поля вокруг квантовых процессов.
Физический смысл я сюда прицеплю позже, а пока рассмотрим обещанный в предисловии «апофеоз» нормировок предложенный Янгом и Миллсом.
Ровелли, как оказалось, был совсем не первый с подобного рода (гнусными) предложениями. Всего-то 50 лет до него Янг и Миллс, оказывается, примерно так-же порезвились со своими «нормировочными полями», правда не по столь глобальному поводу как объединение QFT и GR.
В отличие от Ровелли, их нормировочные поля (loop gauges) имели «конечные нормы», потому что были дискретными – а Ровелли себе этого позволить не мог, потому что как-бы он тогда из них вывел GR? Пришлось-бы применять Ли-группы – а там сплошные неопределённости…
Некоторое конечное число «круговых нормировок» дискретного поля частицы («спинового поля») у Янга-Миллса составляли орто-нормальный базис состояний частицы в Гильбертовом пространстве состояний.
Проще говоря, разрешённые состояния частицы определялись конечным числом состояний окружающих её калибровочных «спинорных полей». Но эти «спинорные поля», в свою очередь, не были независимыми. Они возникали как результат «калибровочной процедуры» (иногда «gauge» переводится как «измерительная процедура» в Фарадеевском смысле, то есть взаимо-воздействие) – результат взаимодействия между частицей и сгенерированным ей (и возможно другими частицами) полем…
Уф… Миллс и Ровелли «чистые математики» и никогда не пошевельнут пальцем чтобы подложить под свои построения хоть какую-то наглядную картину. Ну что-ж, попробуем сделать это за них.
Предположим (вместе с Дираком), что их «поля» это какие-либо состояния физического вакуума.
Ура – наконец-то всё становится на свои места (и мозги тоже).
Частицы и ближайшие к ним узлы вакуума оказывается (по Янгу-Миллсу-Ровелли) обязаны составлять физическое ЕДИНСТВО.
Частица в квантовых процессах «генерирует» в вакууме (спинорном поле, сеточном пространстве – как не назови) – затухающую «замкнутую»(«loop») волну. Кстати, в следующей главе даже у этой «замкнутости» появится физический смысл.
Хотя ведь на английском loop может означать ещё и «обратную связь», обратное воздействие…
И наоборот – следующее состояние в которое может перейти частица будет определятся состоянием этой loop-волны (в вакууме).
Шутка юмора в том, что Дирак говорил, что электрические свойства частиц являются «возбуждёнными состояниями» окружающего её вакуума – а Янг-Миллс-Ровелли замахнулись уже на самое святое – на гравитационные и пространственно-временные её свойства. И как ни странно и у Дирака и у Миллса всё выглядит очень похоже на правду (:0).
То есть вообще все (!) свойства частиц являются «возбуждёнными состояниями» вакуума?!
Ну ваще…
Хым-м-м.. а может никаких «частиц» на самом деле и нету, а есть только «возбуждённые» состояния вакуума?
--- <> ---
Наши (так и тянет сказать «бесстрашные») русские специалисты в области ТТТ (Шипицын – Живодёров – Горбич [3]) пришли к аналогичной идее как мне кажется совершенно без всякого влияния со стороны Дирака и Янга-Миллса (:0).
У них в распоряжении была Теория Твёрдого Тела (ТТТ) – зачем им какие-то Янг и тем более Миллс?
Они предположили, что «вакуум», как единое целое, можно считать чем-то вроде «кристалло-подобной» структуры.
А различные виды «дефектов» этой кристаллической структуры можно считать тем, что традиционно называется «ядерными частицами».
На первый взгляд эта идея кажется слишком дерзкой.
Но если «приглядется» - она ничем не противоречит идеям Дирака-Янга-Миллса и даже помогает устранить некоторые их проблемы.
Взгляните с близкого расстояния на ваш плоский монитор. Вы разглядели там «сеточное поле»? Попробуйте слегка нажать на экран – заметили как от вашего пальца расходятся какие-то статические волны? (На мониторах с очень мелким зерном эффект трудно обнаружить). Я вас поздравляю – вы обнаружили простейшую модель гравитационного поля…
А теперь представьте что Поле Вакуума имеет какое-то постоянное внутреннее давление (сжатие) между плакеонами…
Мне не очень хочется начинать дискуссию о природе этого сжатия – вполне подойдёт какой-нибудь «космогонический» процесс, например внутренняя тенденция всех планкеонов к расширению. Если эта гипотеза кажется вам скучной – вообразите что «Big Bang» всё-таки был – кто-то очень большой чем-то шарахнул по тому «сверх-дисплею» на экране которого мы все и живём (возможно что благодаря этому удару все частицы и образовались)(:0). Шучу конечно…
Итак, планкеоны в нормальном состоянии «предсжаты».
Второе предположение. Наше сеточное пространство «неоднородно». Очень красиво было-бы сказать что в математическом смысле (как у Янга-Миллса) – но к сожалению в самом тривиальном – среди ячеек сетки есть какие-то дефекты…
С точки зрения ТТТ дефекты в кристаллах это вполне обычное дело. Простейший вариант дефекта в кристалле – это просто «дырка» (вакансия). Ближайшие к вакансии планкеоны поменяют своё напряжённо-деформированное состояние на более «расслабленное» - так что в статическом пределе мы увидим что-то похожее на Рис.1.
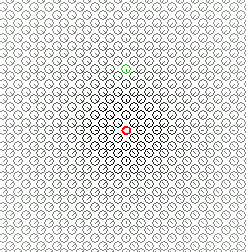
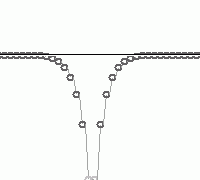
Рис.1. Деформация поля планкеонов с дефектом в центре.
Ниже диаграмма скаляра тензора деформации по центральной оси.
Если вам это ещё ничего не напомнило – я подскажу – это гравитационное поле…
Разумеется это пока ещё очень упрощённое изложение идей Шипицина-Живодёрова. На самом деле они предположили, что дефект это не просто «вакансия» - дефекты тоже имеют какую-то внутреннюю стуктуру. Под первым слоем планкеонов («калибровочных частиц») по их мнению находится как минимум ещё один структурный уровень.
Сравнивая это с тем, что на сегодняшний день считается «догматом веры», я имею в виду «кварки и глюоны», - я вижу со стороны Шипицина-Живодёрова только одно «упущение» - они не упомянули о «глюонах». Сначала я хотел приравнять «глюоны» к калибровочным частицам Янга-Миллса – но теперь понимаю что «глюоны» не стоит вытаскивать на один структурный уровень выше – для них найдётся работа и на более низком уровне – например в качестве «магнитной среды». Но об этом где-нибудь в других главах…
Их дальнейшие «спекуляции» - относительно «кваркового» уровня - уже были вполне «религиозными». На момент когда я читал их сайт ([3]), они остановились на «трёхкомпонентной» структуре кварков (внутренней структуре планкеонов). Это позволило им в основных чертах повторить достижения «Квантовой Хромодинамики». Но результат был достигнут значительно проще – без подключения 32-мерных пространств…
Но давайте пока временно забудем, что «дефекты» вакуума на самом деле имеют какую-то внутреннюю структуру, и обсудим те результаты, которые даёт нам упрощённая модель (с простой «вакансией» на месте дефекта).
Несмотря на всю простоту такой модели, она тем не менее позволяет нам объяснить как работает гравитация (практически во всех деталях).
Для тех кто хотел-бы понять как работает эта модель на более простой аналогии – я могу предложить сравнить это с пузырями воздуха в воде. Одиночный пузырёк воздуха всплывает в градиенте плотности (давления) воды. А теперь остаётся напомнить, что дефекты тоже создают изменения плотности в своей «среде». И другие дефекты будут испытывать притяжение в их градиентных полях.
Картина такого взаимодействия может быть следующей (смотрите срез модели на Рис.2):
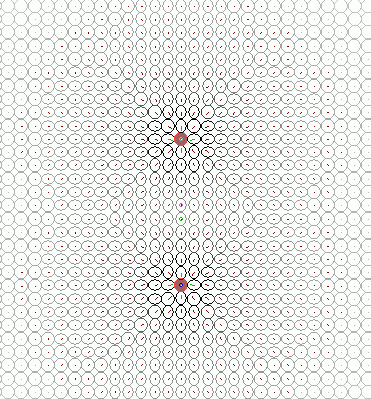
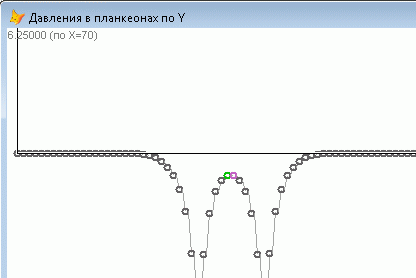
Рис.2. Гравитационное взаимодействие двух вакансий.
Еще одним результатом такой упрощённой модели может быть объяснение эквивалентности между тяжёлой и инертной массами. Объяснение, которое даётся в модели Янга-Миллса в общих чертах то же самое (:0) – я имею в виду объяснение гравитации с помощью калибровочных полей и частиц нарушающих их «калибровочную симметрию».
Поскольку масса в обоих случаях является «нарушением симметрии калибровочных полей» - не имеет значение по внешним (инерционным) или по «внутренним» (гравитационным) причинам эта симметрия была нарушена.
«Тяжёлая» (гравитационная) масса проявляется при ускорении вакансии во внешнем гравитационном поле (Земли).
«Инерционная» масса проявляется при НЕ-гравитационном ускорении той-же самой вакансии – таким образом для достижения точно такого-же ускорения (g) в каком-либо направлении (например параллельно поверхности земли) внешняя «сила» (электромагнитная например) вынуждена будет создать такую же по величине «асимметрию» гравитационного поля вакансии.
Как вы видите на диаграмме во второй половине Рис.2. – деформационные поля от каждой вакансии складываются и в общей центральной части возникает общая «асимметрия», которая объясняет природу гравитационного притяжения двух частиц.
Промоделировать точно такую-же ассиметрию за счёт «электромагнитного возмущения» мне пока достаточно сложно (:0).
--- <> ---
Вот с этого места наша история становится уже не такой «гладкой». Основное отличие нашей русской версии ваккума от вакуума Янга-Миллса, как я уже говорил, состоит в позиции «калибровочного поля» по отношению к частицам.
Частицы Янга-Миллса являются «чем-то внешним» по отношению к «вакууму» их калибровочных полей. И в отсутствии сил и ускорений их частицы могут совершать обычное «равномерное движение».
Мои дерзкие соотечественники, объединив вакуум и частицы, теперь уже просто вынуждены были «запретить» равномерное движение. Ну если Планку было разрешено квантовать энергию (резать её на дискретные части) – то почему моим соотечественникам нельзя позволить «нарезать на части» равномерное движение? Опять дискриминация? (:0).
Таким образом частицы, являясь всего-лишь дефектами вакума, могут «иммитировать» равномерное движение только «интегрально», с точки зрения структурного уровня электронов на орбите атома, например. Поскольку между ними (размером планкеона и орбитой электрона в атоме) разница минимум на пять порядков…
Разумеется внутренние механизмы этих «скачков» вакансий – пока не совсем ясны.
Наши специалисты по ТТТ предпочитают объяснять их в терминологии «диффузия дефекта» в кристалло-подобной среде и т.п.
Возможно это станет понятнее когда появится сколько-нибудь внятная физическая (а не математическая) модель «кваркового» уровня дефектов.
А пока можете считать такое движение результатом простой «рекомбинации» вакансии с соседним планкеоном.
Узлы решётки пространства разумеется не могут оставаться в «абсолютном покое» - есть предположение что решётка всё-время чуть-чуть дрожит («реликтовое излучение»). Возможно это даёт достаточный уровень «стохастики» для появления ненулевой вероятности спонтанных «рекомбинаций» дефектов и планкеонов. А отсюда уже недалеко и до «равномерного движения» в случае приложения какого-то «внутреннего статического потенциала асимметрии» к такому полю.
Возможно кому-то это станет понятнее, если ввести понятие «подвижность» дефекта (по аналогии с подвижностью электрона в плотной среде).
Электрон даже при наличии «подвижности» не начинает равномерного движения пока к среде не будет приложен электрический потенциал. Кстати, аналогия-то достаточно прямая, поскольку электрон это как-раз и есть наша частица (дефект) – только в данном случае мы говорим не о электромагнитной а о «гравитационной подвижности». Хотя ещё неизвестно есть ли между ними принципиальные отличия для частиц с зарядом…
Различный внешний потенциал приведёт к различной скорости «дрейфа» электрона (это я говорю про ТТТ а не про вакуум). Значит нам остаётся только найти для дефектов вакуума те же параметры, которые определяют их подвижность в макро-средах – и сделать перенос «по аналогии». Хотя эта идея может и не сработать на кварковых уровнях (:0).
Итак, мы с вами, читатель, всего-лишь компактная группа «дефектов» загадочным образом плывущая как единое целое по решётке вакуума… Ну и как ощущения? (:0).
--- <> ---
ГЛАВА ВТОРАЯ
Динамические переходные процессы на решётке вакуума
В предыдущей главе мы «постулировали», что вместо равномерного движения наши «вакансии» могут двигаться только скачками – от одного сеточного узла (планкеона) к другому (на его место).
Одним из возможных механизмов такого скачка может быть «рекомбинация» дефекта и планкеона (калибровочной частицы, если использовать терминологию Янга-Миллса).
Мной были предприняты попытки моделирования таких скачков (и их последствий) в поле планкеонов. Модель разработана в логике «клеточных автоматов», то есть каждый нод взаимодействует только с теми ближайшими с которыми он в непосредственном контакте – дальнодействие запрещено.
Одной из серьёзных проблем такой модели является качественная предварительная оценка энергии выделяемой при скачке (и соответственно энергии возникающего при этом переходного процесса).
Если скачок моделируется как «мгновенный», то в «калибровочном поле» возникает слишком большая волна переходного процесса. Разумеется при моделировании с каким-либо реальным шагом эта волна всё-равно сглаживается, но это как раз, в том числе, и вопрос о том какой шаг моделирования нужно выбрать…
Подозреваю что в реальности эта рекомбинация - это тоже процесс (по крайней мере на структурном уровне «кварков»).
А значит импульс переходного процесса значительно уменьшается…
Мы с коллегами также обсуждали вопрос о возможной «энергетической замкнутости» такого перескока. К сожалению к моменту написания этого «обратного перевода» наши дискуссии пока не закончены (:0).
Если вы считаете что «нарушение» принципа «сохранения энергии» является основным аргументом против такой модели – я могу возразить, что дополнительную энергию для начала рекомбинации дефект берёт из изначально предсжатого состояния поля планкеонов… Как я уже «настаивал» выше – изначальный («первичный») вакуум должен содержать огромное количество энергии «закачанной» туда при его «космогоническом сжатии»… Ну да, разумеется «неподтверждённая гипотеза» (:0).
В любом случае (даже если причина перескока чисто «стохастическая») – перескок породит переходный процесс в окружающих планкеонах. Как в любом виде «распределённых сред», переходный процесс будет напоминать «волну». Но в данном случае НЕ просто сферическую…
Поскольку это волна в «калибровочном гравитационном поле» - то можете рассматривать её как «локальную гравитационную волну». И полюбоваться на неё на Рис.3.:

Рис.3. Реакция поля планкеонов на скачок дефекта.
Скачок дефекта произошёл в центре картинки, сверху вниз.
Синим цветом – бегущие вперёд волны ослабления тензора сжатия,
Красным цветом – бегущие назад волны возвращения в исходное сжатие.
В нижней части – ещё один дефект и волна там замедляется
(но это НЕ «граничный эффект» – поле модели намного шире)
(к тому же в модели добавлено подавление граничных эффектов)
Сразу после скачка формируется нечто вроде «динамического гравитационного диполя». В направлении перескока начинает распространятся волна ослабления тензора сжатия (деформации) поля планкеонов. В обратном направлении распространяется волна частичного «возврата в исходное сжатое состояние». В этом смысле это «анизотропная» волна.
Математически «анизотропные» волны описываются совершенно иначе чем обычные сферические…
Это уже будет описание переходного процесса от внезапно возникшего «динамического диполя» в качестве источника.
В отличие от сферической волны, у нашей волны будет нечто вроде «спина» - выделенной оси особых точек на перпендикуляре к вектору перескока. Возможно при рассмотрении с точки зрения фрактальной геометрии, такому «спину» удалось бы приписать «размерность» =1/2 (:0).
Завершая обсуждение энергетического балланса перескока дефекта, можно ещё сказать, что практически весь начальный импульс перейдёт к тому планкеону, который встал на старое место дефекта – таким образом большая часть энергии скачка переходит во внутреннюю «стохастическую» энергию самой сетки (реликтовое излучение). Ну а небольшой остаточек будет добавлен к «массе» (деформированному состоянию поля планкеонов от этого дефекта). И не исключено, что эта добавка будет расти с увеличением (средней) скорости перескока. Хотя это ещё надо проверять (пусть Эйнштейн не обижается).
А теперь возможно самое время вспомнить про «уравнения Хевисайда» (Heaviside, 1893).
По виду они были полностью аналогичны уравнениям Максвелла, только электрическое поле (Е) в них было заменено на «поле массы» (гравитационное), а магнитное поле (В) было заменено на «гиро-гравитационное». С соответствующей заменой констант «проводимости» и т.п.
Хевисайд также предположил, что источником таких волн должен быть «какой-то диполь»…
Разумеется наша модель ещё далека от полноты физической картины – туда пока ещё не добавлено рассмотрение переходного процесса в «магнитной среде» после скачка дефекта. Но в отличие от «динамического гравитационного диполя» - вторая половина электрического диполя находится не рядом с перепрыгнувшим дефектом – а где-то на отдалённых других дефектах – а значит в самом общем случае одиночный перескок «вдали от других зарядов» не вызывает значительного переходного процесса в магнитной среде (?). Но ещё предстоит оценить, что в данном случае считать «вдали»? Ведь электромагнитные взаимодействия в чудовищное количество раз сильнее гравитационных…
Обсуждение динамических процессов в «магнитной среде» перенесено в третью главу книги. А здесь пока продолжим обсуждение переходных процессов от скачка дефекта - в поле планкеонов (гравитационном).
--- <> ---
Как же мы можем пропустить такую интересную тему, как «резонанс электрона на двух щелях»? (:0).
Это про то как электрон «одновременно проходит» через две рядом расположенные тонкие щели, оставляя на детекторах интерференционную картину (при детектировании большого числа одиночных прохождений).
