ЛАБОРАТОРНАЯ РАБОТА №2
Действительные числа. Метод математической индукции. Абсолютная величина.
Опр.1. Числа 1, 2=1+1, 3=2+1,…n-1,n=(n-1)+1… называется натуральными. Таким образом, множество натуральных чисел может быть определено как наименьшее – числовое множество, содержащее число 1 и вместе с каждым числом n содержащее число n+1.
Метод математической индукции: если предложение, зависящее от натурального числа n:
а) верно для некоторого начального значения n=n 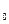 , например, n=1;
, например, n=1;
б) из допущения, что оно верно для n=k, где k 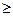 n
n 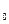 произвольное натуральное число, вытекает, что предложение верно и для n=k+1, то предложение верно при любом натуральном n
произвольное натуральное число, вытекает, что предложение верно и для n=k+1, то предложение верно при любом натуральном n 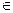 N.
N.
Пример 1. Доказать, что верно равенство:
1  +2
+2  +…+n
+…+n  =
= 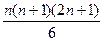 (1).
(1).
Решение: 1.  ] n=1, тогда (1
] n=1, тогда (1  =1)
=1) 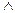 (
( 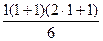 =
= 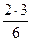 =1), 1=1.
=1), 1=1.
Действительно, равенство верно при n=1.
2. Допустим, что равенство (1) верно при n=k.
3. Докажем верность равенства (1)при n=k+1:
1  +2
+2  +3
+3  +…+k
+…+k  +(k+1)
+(k+1)  =(1
=(1  +2
+2  +…+k
+…+k  )+(k+1)
)+(k+1)  .
.
Т.к. равенство верно при n=k, то (1  +2
+2  +…+k
+…+k  )+(k+1)
)+(k+1)  =
= 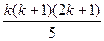 +(k+1)
+(k+1)  =(k+1)[
=(k+1)[ 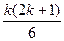 +(k+1)]=(k+1)
+(k+1)]=(k+1) 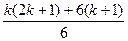 =(k+1)
=(k+1) 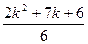 .
.
Разложим 2k  +7k+6 на множители, для этого найдем его нули:
+7k+6 на множители, для этого найдем его нули:
2k  +7k+6 =0
+7k+6 =0
D=49-48=1>0 k 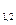 =
= 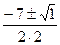 ; k
; k 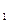 =
= 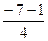 =-2, k
=-2, k 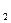 =
= 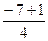 = -
= - 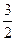
Значит, 2k  +7k+6= 2(k+2)(k+
+7k+6= 2(k+2)(k+ 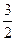 )=(k+2)(2k+3)
)=(k+2)(2k+3)
Таким образом, 1  +2
+2  +3
+3  +…+k
+…+k  +(k+1)
+(k+1)  =
= 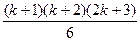 ,
,
Т.е. равенство (1) верно при n=k+1. Значит, это равенство верно при
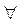 n
n 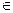 N
N
Опр.2. Множество R называется множеством действительных чисел, а его элементы x 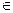 R - действительными числами, если выполняется следующий набор аксиом: (см. В. А. Зорич «Математический анализ» стр. 45)
R - действительными числами, если выполняется следующий набор аксиом: (см. В. А. Зорич «Математический анализ» стр. 45)
I. Аксиомы сложения (?).
II. Аксиомы умножения (?).
III. Аксиомы связи сложения и умножения (?).
IV. Аксиомы порядка (?).
V. Аксиомы связи сложения и порядка (?).
VI. Аксиомы связи умножения и порядка (?).
VII. Аксиомы полноты (?).
Опр.3. Абсолютной величиной (модулем) числа x 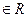 называется число |x|, определяемое условиями: |x|=
называется число |x|, определяемое условиями: |x|= 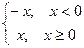
Свойства абсолютных величин:
1. 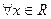 , |x|
, |x| 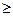 0
0
2. 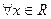 , |x|=|-x|
, |x|=|-x|
3. 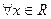 , x
, x 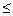 |x|, -x≤|x|
|x|, -x≤|x|
4. 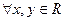 , |x+y|≤|x|+|y|
, |x+y|≤|x|+|y|
5. 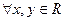 , | |x|-|y| |≤|x-y|.
, | |x|-|y| |≤|x-y|.
6. 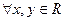 , |xy|=|x| |y|.
, |xy|=|x| |y|.
Неравенство |x|≤ 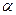 означает, что -
означает, что - 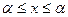 .
.
Неравенство |x| 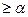 означает, что (x
означает, что (x 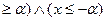 .
.
Пример 2. Решить неравенства: а) |2x-1|<1,
б) |x  -8x+12|>x
-8x+12|>x  -8x+12.
-8x+12.
Решение: а) неравенство |2x-3|<1 равносильно неравенствам –
1<2х-3<1, откуда 2<2x<4 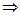 1<x<2.
1<x<2.
Ответ: (1,2).
б) данное неравенство справедливо для тех значений х, при которых x  -8x+12<0. Найдем нули квадратного трехчлена:
-8x+12<0. Найдем нули квадратного трехчлена:
x  -8x+12=0
-8x+12=0
(x 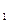 +x
+x 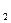 =8)
=8) 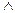 (x
(x 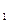 x
x 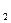 =12)
=12) 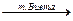 (x
(x  =2)
=2) 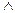 (x
(x 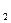 =6)
=6)
Таким образом, x  -8x+12=(х-2)(х-6). Решаем методом интервалов:
-8x+12=(х-2)(х-6). Решаем методом интервалов:

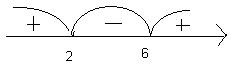
Ответ: (2,6).
Пример 3. Имеет ли решение уравнение: |x|=x+5
Решение: при х 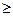 0 имеем х=х+5, решений нет. При х<0 имеем –х+х+5=0
0 имеем х=х+5, решений нет. При х<0 имеем –х+х+5=0 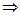 , х=
, х= 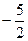 . Это значение удовлетворяет исходному уравнению.
. Это значение удовлетворяет исходному уравнению.
Ответ: х= 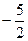 .
.
ВАРИАНТЫ
1. Доказать равенство:
1) 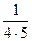 +
+ 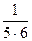 +
+ 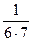 +…+
+…+ 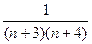 =
= 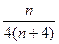
2) 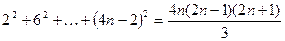
3) 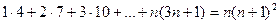
4) 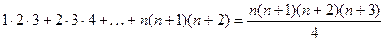
5) 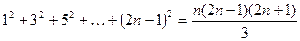
6) 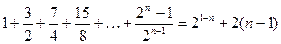
7) 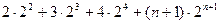 =
= 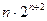
8) 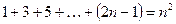
9) 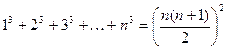
10) 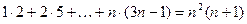
11) 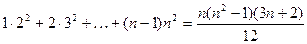
12) 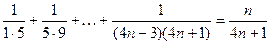
13) 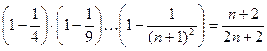
14) 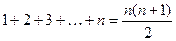
15) 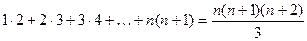
16) 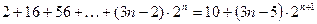
17) 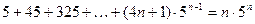
18) 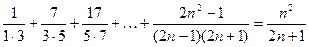
19) 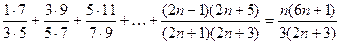
20) 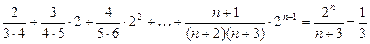
21) 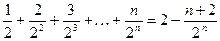
22) 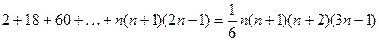
23) 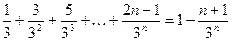
24) 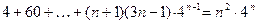
25) 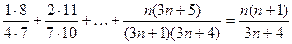
2. Доказать, что для 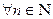 справедливо утверждение:
справедливо утверждение:
1) 6 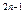 +1 кратно 7 2) 7
+1 кратно 7 2) 7 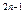 -1 кратно12
-1 кратно12
3) 4  +15n-1 кратно 9 4) n
+15n-1 кратно 9 4) n  -n является четным
-n является четным
5) 5 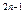 +1 кратно 6 6) 9
+1 кратно 6 6) 9 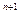 -8n-9 кратно 16
-8n-9 кратно 16
7) 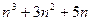 кратно 3 8) 3
кратно 3 8) 3 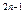 +1 кратно 4
+1 кратно 4
9) 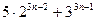 кратно 19 10)
кратно 19 10) 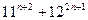 кратно 133
кратно 133
11) 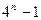 кратно 3 12)
кратно 3 12) 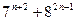 кратно 57
кратно 57
13) 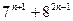 кратно 19 14)
кратно 19 14) 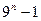 кратно 8
кратно 8
15) 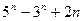 кратно 4 16)
кратно 4 16) 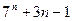 кратно 9
кратно 9
17) 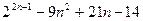 кратно 27 18)
кратно 27 18) 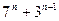 кратно 4
кратно 4
19) 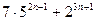 кратно 17 20)
кратно 17 20) 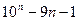 кратно 81
кратно 81
21) 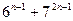 кратно 43 22)
кратно 43 22) 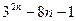 кратно 16
кратно 16
23) 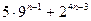 кратно 7 24) n3+5n кратно 6
кратно 7 24) n3+5n кратно 6
25) 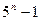 кратно 4
кратно 4
3. Решить уравнение и неравенство:
1) |3x-2|=0,3; |3x-5|-|2x+3|>0
2) |2x+2,5|=|x-3,3|; 2x  -5|x|+3
-5|x|+3 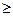 0
0
3) |2x+3|=0,1; |x  -5x|>|x
-5x|>|x  |-|5x|
|-|5x|
4) |x+4|=|x-4|; x  -2|x|-3>0
-2|x|-3>0
5) |x+7|=|x-2|+|x-3|; x  -4|x|+3>0
-4|x|+3>0
6) x  -2|x|-3=0; |x|
-2|x|-3=0; |x| 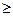 |x-2|
|x-2| 
7) |sinx|=sinx+1; |x-5|<|x-1|
8) |2x+1|=3; |x-1|<|x+1|
9) |x-2|+|x-4|=3; |4x+5|<3
10) 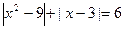 ;
; 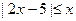
11) 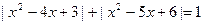 ; |x2-4|<3x
; |x2-4|<3x
12) |x2-x-5|=1; 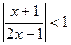
13) x2-|x|-2=0; |3x-2|>|2x+1|
14) 2(x-1)2+|x-1|-1=0; 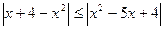
15) x|x|+8x-7=0; 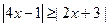
16) |x-2|x-6x+8=0; x2-4|x|<12
17) x2-2|x-1|=2; |x+1|+|x-1| 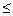 2
2
18) |x+3|=x2+x-6; 2|x-3|+|x+1| 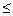 3x+1
3x+1
19) |x2+x-1|=2x-1; |3x-2|x<1
20) |x-1|+|x+2|-2x=1; 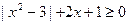
21) 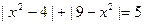 ; |x2+x-2|>
; |x2+x-2|> 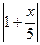
22) |5-3x|=2x+1; 3x+|2-x| 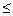 5
5
23) x2-7=|3x-7|; 3x>2-|3-x|
24) x|3x+5|=3x2+4x+3; 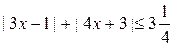
25) |3x-8|-|3x-2|=6; 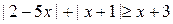
ЛАБОРАТОРНАЯ РАБОТА № 3.
