Теоретическое обоснование. Лабораторная работа 1

Лабораторная работа 1

ОСНОВЫ РАБОТЫ В СРЕДЕ MATLAB (4ч)

Цель и содержание работы:научиться проводить прямые вычисления и создавать М-файлы в пакете автоматизации математических расчетов MATLAB.

Теоретическое обоснование

MATLAB(MATrix LABoratory – матричная лаборатория) – является системой автоматизации математических расчетов, построенной на расширенном представлении и применении матричных операций. В MATLAB используются такие типы данных, как многомерные массивы, массивы ячеек, массивы структур и разреженные матрицы, что открывает возможности применения системы при создании и отладке алгоритмов матричных вычислений и крупных баз данных.

Двумерный массив чисел или математических выражений принято называть матрицей, а одномерный массив называют вектором. Размер матрицы определяется числом ее строк m и столбцов n (указывают как 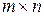). Примеры вектора и матрицы: 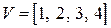– вектор из 4 элементов; 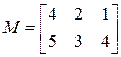– матрица размера 2x3.

Обычные числа и переменные в MATLAB рассматриваются как матрицы размера 1x1, что дает единообразные формы и методы проведения операций над обычными числами и массивами. Данная операция обычно называется векторизацией. Векторизация обеспечивает и упрощение записи операций, производимых одновременно над всеми элементами векторов и матриц, и существенное повышение скорости их выполнения.

Система MATLAB выполняет сложные и трудоемкие операции над векторами и матрицами даже в режиме прямых вычислений без какого-либо программирования. В этом случае работа происходит в режиме «вопрос – ответ», что напоминает работу в MathCAD. Ею можно пользоваться как мощным калькулятором, в котором наряду с арифметическими и алгебраическими действиями могут использоваться сложные операции: инвертирование матрицы, вычисление ее собственных значений и принадлежащих им векторов, решение систем линейных уравнений, вывод графиков двумерных и трехмерных функций и многое другое.

В режиме непосредственных вычислений, которые проводятся в командном режиме, можно решать множество математических задач.

Существует ряд основных команд управления Окном командного режима (Command Window):

clс– очищает экран и размещает курсор в левом верхнем углу пустого экрана;

home– возвращает курсор в левый верхний угол окна;

mоrе on – включает режим постраничного вывода (полезен при просмотре больших m-файлов);

mоrе off – отключает режим постраничного вывода (в этом случае для просмотра больших фалов надо пользоваться линейкой прокрутки).

В системе MATLAB можно задавать переменным определенные значения. Для этого используется операция присваивания, вводимая знаком равенства, аналогично присваиванию в Visual Basic.

Типы переменных заранее не декларируются и определяются выражением, значение которого присваивается переменной. Например, если выражение – вектор или матрица, то переменная будет векторной или матричной.

Имя переменнойможет содержать сколько угодно символов, но запоминается и идентифицируется только 31 начальный символ. Имя любой переменной не должно совпадать с именами других переменных, функций и процедур системы. Имя должно начинаться с буквы, может содержать буквы, цифры и символ подчеркивания. Недопустимо включать в имена переменных пробелы и специальные знаки, например +, .-, * и т. д.

Существует ряд основных правил для общения с MATLAB:

- для указания ввода исходных данных используется символ >>;

- для блокировки вывода результата вычислений некоторого выражения после него надо установить знак «;» (точка с запятой);

- если не указана переменная для значения результата вычислений, то MATLAB назначает такую переменную с именем ans;

- знаком присваивания является знак равенства =;

- результат вычислений выводится в строках вывода (без знака >>);

- встроенные функции (например, sin) записываются строчными буквами, и их аргументы указываются в круглых скобках;

Оператор – это специальное обозначение для определенной операции над данными – операндами. Используются следующие операторы:

+сложение;

- вычитание;

* умножение;

.* поэлементное умножение массивов;

/деление;

./ поэлементное деление массивов;

\ левое деление (деление справа налево);

^ возведение в степень;

‘ транспонирование

( ) определение порядка вычислений.

Система MATLAB предоставляет большое количество элементарных математических и логических функций, функций обработки множеств и т.д. Несколько специальных функций являются значениями часто используемых констант:

аns – результат выполнения последней операции;

pi – 3.14159265…;

i или j – мнимая единица ( );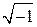

eps – относительная точность числа с плавающей точкой, 2^-52;

realmin – наименьшее число с плавающей точкой, 2^-1022;

realmax – наибольшее число с плавающей точкой, ;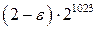

Inf – бесконечность, NAN – не число.

В системе MATLAB определены следующие функции (таблица 1.1).

Таблица 1.1 – Основные функции MATLAB

Функция	Название	Пример
Математические
abs(X)	Модуль.для каждого числового элемента вектора X.	>> abs(-5) ans =
ехр(Х)	Экспонента. Возвращает экспоненту для каждого элемента X.	>> ехр([1 2 3]) ans = 2.7183 7.3891 20.0855
inv(A)	Возвращает матрицу А-1, обратную матрице А	A = 1 2 3 5 7 8 3 4 9 >> inv(A) ans = -2.2143 0.4286 0.3571 1.5000 0.0000 -0.5000 0.0714 -0.1429 0.2143
det(A)	Возвращает определитель матрицы А	>> det(A) ans = -14
log(X)	Возвращает натуральный логарифм элементов массива X.	>> Х=[1.2 3.34 5 2.3]; >> log(X) ans= -0.1823 1.2060 1.6094 0.8329
log2(X)	Возвращает логарифм по основанию 2 элементов массива X.	>> log2(X) ans = 0.2630 1.7398 2.3219 1.2016
log10(X)	Возвращает десятичный логарифм элементов массива X.	>> log10(X) ans = 0.0792 0.5237 0.6990 0.3617
sqrt(А)	Возвращает квадратный корень каждого элемента массива А	>> А=[25 21.23 55.8 3]: >> sqrt(A) ans = 5.0 4.6076 7.4699 1.7321
cos(X)	Косинус для каждого элемента X	>> X=[1 2 3]; >> cos(X) ans = 0.5403 -0.4161 -0.9900
acos(X)	Возвращает арккосинус для каждого элемента X	>>Y = acos (0.5) Y= 1.0472
sin(X)	Возвращает синус для каждого элемента X	>> X=[pi/2 pi/4 pi/6 pi]; >> sin(X) ans = 1.000 0.7071 0.500 0.000
asin(Y)	Арксинус для каждого элемента Y	>> Y= asin (0.278) Y = 0.2817

Продолжение таблицы 1.1

Функция	Название	Пример
tan(X)	Тангенс для каждого элемента X	>> Х=[0.08 0.06 1.09] >> tan(X) ans= 0.802 0.0601 1.9171
atan(Y)	Возвращает арктангенс для каждого элемента Y	>> Y=atan(1) Y = 0.7854
mod(X,Y)	Возвращает остаток от дедения X на Y	>> mod(5,2) ans =
Функции и операторы отношения Данные операторы выполняют поэлементное сравнение векторов или матриц одинакового размера и возвращают значение 1 (True), если элементы идентичны, и значение 0 (False) в противном случае.
eq	Равно. Оператор: = =	>> eq(2, 2) ans = >> 2==2 ans =
ne	Не равно. Оператор: ~ =	>> ne(l, 2) ans = >> 2 ~- 2 ans =
Lt	Меньше чем. Оператор: <	x<y
Gt	Больше чем . Оператор: >	x>y
Le	Меньше или равно. Оператор: <=	x<=y
Ge	Больше или равно. Оператор: >=	x>=y
Логические операторы и функции
And	Логическое И (AND) &	»А=[1 2 3]; »В=[1 0 0]; » and(A.B) ans = 1 0 0
Or	Логическое ИЛИ (OR) |	>> оr(А.В) ans = 1 1 1
Not	Логическое НЕ (NOT) ~	>> not(B) ans = 0 1 1

При решении сложных задач возникает необходимость сохранения полученных вычислений и их дальнейшей модификации. Файлы, которые содержат код на языке MATLAB, называются М-файлами. Существует два вида М-файлов:

- файлы-сценарии, которые не имеют входных и выходных аргументов;

- файлы-функции, которые имеют входные и выходные аргументы.

Файл-сценарий, именуемый также Script-файлом, является просто записью серии команд без входных и выходных параметров. Он работает с данными из Рабочей области (Workspace), в процессе работы не компилируется и представляет собой зафиксированную в виде файла последовательность операций, полностью аналогичной той, что используется при прямых вычислениях. В MATLAB можно использовать комментарии, которые должны начинаться с символа %. При правильной записи комментария он выделяется зеленым цветом, в противном случае – красным.

Файлы-функции – это М-файлы, которые имеют входные параметры и возвращают выходные. Имя М-файла и имя функции должно быть одним и тем же. Функции работают с локальными переменными в пределах их собственного рабочего пространства. Первая строка файла-функции начинается со слова function. Здесь происходит задание имени функции со списком входных и выходных аргументов. Остальные строки файла представляют собой исполняемый код MATLAB. Например, на рисунке 1.1 представлен файл-функция fun двух переменных х и у, вычисляющая .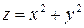

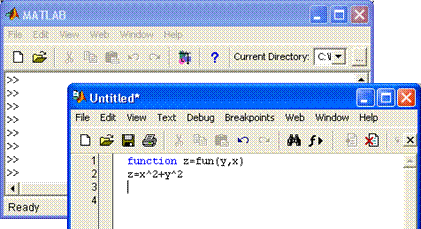
Рисунок 1.1 – Создание файла-функции

Если функция имеет несколько выходных параметров, то эти параметры записываются в квадратных скобках перед именем функции через запятую в той последовательности, в которой они будут возвращаться. Синтаксис записи такой функции выглядит следующим образом:

function [Выходные_параметры]=f_name (Список_входных_параметров)

Функцию можно вызывать как из файла-сценария, так и в режиме прямых вычислений.

Аппаратура и материалы:ПК не ниже Pentium II, OC семейства Windows, математический пакет MATLAB 7.

Техника безопасности

Соблюдать требования по охране труда при работе в компьютерных классах (инструкция № 140).

Задания

1. Ознакомиться с интерфейсом системы MATLAB. Изучить правила ввода матриц и векторов, использования операторов.

2. В режиме прямых вычислений двумя методами (методом Крамера и матричным методом) решить систему линейных уравнений:

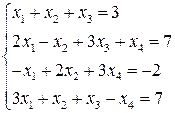
3. Решить приведенную выше систему уравнений путем создания М-файлов.