Свойства неопределенного интеграла

1. (òf(х)dх)'= f(х)

2.dòf(х)dх)'=f(х)dх

3. òdF(х)=F(х)+С

4. òkf(х)dх=kòf(х)dх, k¹0.

5. ò(f(х)±g(х))dх= òf(х)dх±òg(х))

Таблица основных неопределенных интегралов.

1. ò0dх=С.

2. 2.òхdх= х+С.

3. 3. òх^adх= 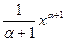+С, a¹1.

4. òсоsхdх=sinх+С; 5. òsinхdх= –соsх+С;

6. ò 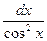=tgх+С; 7. ò 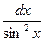=-сtgх+С;

8. ò 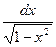= 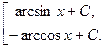; 8а. ò = ;

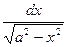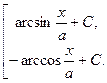9. ò 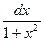= 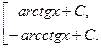; 9а. ò = ;

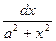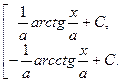10. òа^хdх= а^х/lnх+С; 10а. òе^хdх= е^х + С;

11. ò 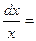ln|х|+С;12. ò 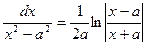+С; 13 ò 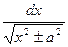=ln|х+ 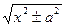|+С

Задача о площади (площадь криволинейной трапеции).

y=f(x) – [a; b], f(x)≥0

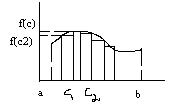
Найти S:

Для решения, разобьем [a; b] на n частичнымх отрезков [xk; xk+1]; a=x0<x1<…<xn=b.

Эти точки xk – разбиение [a;b].

Внутри кажд. частичного отрезка выберем точку Ck принадлеж. [xk; xk+1] и найдем знач. ф-ии в Ck

f(ck),k=0,…n-1

Sn – площаль всех прямоуг-ов: Sn=(x1-x0)f(c1)+(x2-x1)f(c2)+..+f(xn-xn-1)f(Ck)

xk-xk-1=∆xk

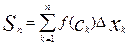(1)

Пусть S – площадь криволин. трапеции, тогда при больших n имеет место приближ рав-во S≈Sn, причем, чем больше отрезков берем, тем точнее рав-во.

Пусть λ=max∆Xk – наиб. из длин частичных отрезков – диаметр разбиения.

Если в (1) перейти к пределу так, чтобы кол-во част. отрез-ов неогран. возрасло и при этом λ->0, то мы получим знач S криволин. трап:

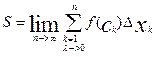
Определенный интеграл.

Определённым интеграломфункции f(х) непрерывной на отрезке [а, b] называется предел интегральной суммы, независящий от дробления отрезка [а, b] на частичные и выбора точек a_i когда наибольшая из длин частичных отрезков стремится к нулю.

Свойства определенного интеграла.

Значение о.и. не зависит от выбора переменной интегрирования:

1.

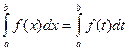
2.

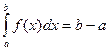
3. 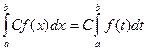С=const

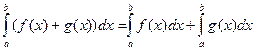
4. 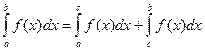для любых a, b, c

5. Если f’(x)>=0, на [a; b] и интегрируема на [a; b ] =>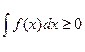

6.f(x)>=g(x), x принадлеж. [a; b], то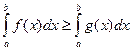

7. пусть f(x) – непрерывна на [a; b ] и m=min f(x), M=max f(x), тогда имеют место неравенства:

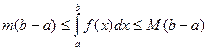
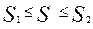
8. Т. О среднем значении если f(x)непрерывна на отрезке [a,b] то сущ.на этом отрезке такая т-ка что ∫_a^bf(x)dx=f(c)(b-a).

Интеграл с переменным верхним пределом и его свойства.

Пусть f(x) непрерывна на отрезке [a,b] тогда она интегрируема на этом отрезке и зн.интегрируема на любом отрезке [a,х] содержащимся в [a,b].

Рассм.ф-цию Ф(х)=∫_а^х f(x)dx- её наз.интегралом с переменным верхним пределом.

Св-ва:

1. Ф(х) непрерывна на [a; b]

2. Если f(x) – непрер. на [a; b], то Ф(х) – дифф-ма на [a; b] и Ф’(x)=f(x).

Формула Ньютона-Лейбница.

Если ф-ция f(х) непрерывна на [a,b] и ф-я F(x) какая-либо первообразная для f(x) на отрезке[a,b] то справедлива формула

.

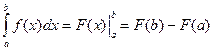Док-во:

пусть F(x)первообразная для f(x) на отрезке [a,b], ф-ция Ф(х) так же явл.первообразной. по теореме о множестве первообразных имеем Ф(х)-F(x)=C. Подставим в последнее рав-во вместо х сначала а, потом b=х получим:

Ф(а)-F(a)=C Ф(b)-F(b)=C Ф(а)=∫_a^a f(x)dx=0 Ф(b)=∫_a^b f(x)dx

Имеем C=-F(a) ∫_a^b f(x)dx+F(a)=F(b) ∫_a^b f(x)dx=F(b)-F(a)

Длина дуги плоской кривой.

Пусть некот. линия y=f(x), где f(x) – дифф. на отрезке [a; b]

Y(k-1) M(k-1)

M1

yk A Mk

M(n-1) B

a=x0 x1 x2 xk x(n-1) b=xn

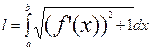- длина дуги АВ