Основные формулы комбинаторики

Перестановкаминазывают комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возмож­ных перестановок

P_n = n!

где n!= 1∙2∙3...п.

Размещенияминазывают комбинации, составленные из п различных элементов по т элементов, которые от­личаются либо составом элементов, либо их порядком. Число всех возможных размещений

.

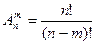Сочетанияминазывают комбинации, составленные из п различных элементов по т элементов, которые отли­чаются хотя бы одним элементом.

Число сочетаний

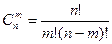
При решении задач комбинаторики используют сле­дующие правила:

Правило суммы. Если некоторый объект Аможет быть выбран из совокупности объектов т способами, а другой объект Вможет быть выбран п способами, то выбрать либо А, либо Вможно т + п способами.

Правило произведения. Если объект Аможно выбрать из совокупности объектов т способами и после каждого такого выбора объект Вможно выбрать п спо­собами, то пара объектов (А, В)в указанном порядке может быть выбрана тп способами.

Случайная величина и закон её распределения

Случайной называют величину, которая принимает в ре­зультате испытания то или иное возможное значение, зара­нее неизвестное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств.

Случайные величины могут быть дискретными и непре­рывными.

Дискретнойназывают такую случайную величину, кото­рая принимает счетное множество значений, т.е. такое мно­жество, элементы которого можно подсчитать.

Непрерывнойназывают такую случайную величину, ко­торая может принимать любые значения в определенном интервале. Занумеровать все значения величины, попадаю­щие даже в узкий интервал принципиально невозможно. Эти значения образуют несчетное бесконечное множество.

Распределение дискретных и непрерывных случайных величин

Случайная величина считается заданной, если известен закон распределения случайной величины.

Распределением (законом) случайной величины называет­ся всякое соотношение между возможными значениями слу­чайной величины и соответствующими им вероятностями.

Таблица, содержащая возможные значения случайной величины и соответствующие вероятности, является простей­шей формой задания распределения дискретной случайной величины:

Значения случайной величины Х	x1	x2	…	xn
Вероятности значений рi	р1	р2	…	pn

р₁ + р₂ + … + p_n = 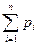= 1.

Табличную формулу задания называют также рядом распределения.