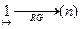Эмпирическая функция распределения

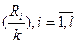
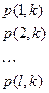
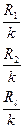
Хи – квадрат.

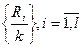
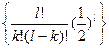
Тест многомерной равномерности.

(x₁, … , x_n)

…………………

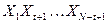
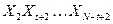
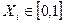
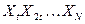
Так как числа распределены по равномерному закону, они все заключены в куб с единичными сторонами.

Вероятность попадания каждой из точек в гиперкубик равна: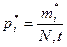

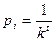
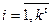
Выбор числа гиперкубиков.

Число гиперкубиков должно быть как можно больше, но при тестировании по критерию Хи – квадрат число должно быть равно 10 ¸ 20 (20 ¸ 30), поэтому существует ограничение на число гиперкубиков.

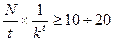, k – количество интервалов, на который разбит гиперкубик.

Сторона гиперкуба.

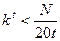
из этой формулы следует, что количество отрезков разделяющих гиперкубик ограничено сверху.

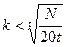, t – число групп.

Тест наибольшей из t.

Разделение последовательности на t групп, N/t – подпоследовательности.

Алгоритм.

В каждой из подпоследовательностей вычисляем максимальное значение.

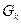
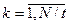
1. максимальное
2. 
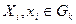
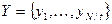
3. рассмотрим вероятность

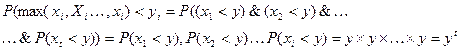
если равномерное распределение

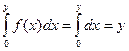
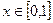
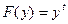
Указанные функции сравниваем по критерию Колмогорова при этом задаются с некоторой доверительной вероятностью a. Если указанные функции совпадают с указанным критерием, то можем судить, что последовательность распределена по нормальному закону.

Серия- это любой отрезок последовательности, который состоит из следующих друг за другом элементов одного вида.

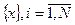
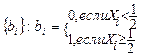
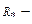число серий

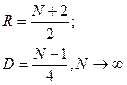
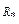
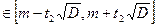
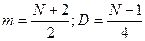
С вероятностью L последовательность можно считать случайной.

Тест монотонности

Последовательность разбиваем на непересекающиеся следующие друг за другом интервалы, элементы которых не убывают и не возрастают.

Пример: 0,30,1 0,5 0,30,70,30,2 0,6 0,70,4

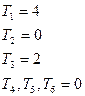T_i-количество подпоследовательностей имеющих длину равную i.

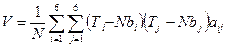
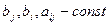
V-статистическая

Тест апериодичности, только для псевдослучайных чисел.

X_i X_i+T X_i+2T

L

Задача: найти X_i,X_i+T

Моделирование случайных воздействий

ДСС

Случайные коды:

1)последовательная схема

ДСС→‎

Достоинства: простота.

Недостатки: высокая задержка.

2)параллельная схема

	ДСС1		RG(n)
		ДССn

®

.

.

Достоинства: быстродействие.

Недостаток: сложность.

3)параллельно-последовательная схема

Соблюдается компромисс между быстродействием и сложностью в зависимости от k.

Программный метод получения псевдослучайных чисел.

1. Метод середины квадрата

1 n

n-разрядное число возвести в степень k, то получим

( )

1 n R_n

n-разрядов, которые мы потом опять возводим в степень R

-выбор n-разрядного числа X.

-y= 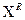- 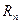разрядное число

-выбор в середине n-разрядов

-переход к 1 шагу, если <N

Метод умножения.

-

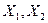
-y=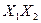

X

( ( ) )

2n

X₁¹ 0,X₂¹0