Обыкновенные дифференциальные уравнения (29)
1. Задачи приводящие к дифференциальным уравнениям:
Условие: тело массой m, падает на поверхность земли с высоты h, найдем закон движения υ(x): 
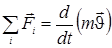 в нашем случае m=const, проектируя это уравнение на ось ОХ получим:
в нашем случае m=const, проектируя это уравнение на ось ОХ получим:
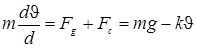 где
где 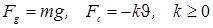 ; или
; или 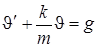 - дифференциальное уравнение 1го порядка.
- дифференциальное уравнение 1го порядка.
Дифференциальное уравнение 1го порядка: Уравнения, связывающее независимую переменную х, функцию у, и ее производную 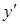 т. е. уравнение вида
т. е. уравнение вида 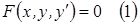 называется дифференциальным уравнением первого порядка (обыкновенные). Порядок дифференциального уравнения определяется порядком производных. Примечание: Обыкновенные дифференциальные уравнения связывает независимую переменную х функцию у и ее производные до n-го порядка включительно и записывают
называется дифференциальным уравнением первого порядка (обыкновенные). Порядок дифференциального уравнения определяется порядком производных. Примечание: Обыкновенные дифференциальные уравнения связывает независимую переменную х функцию у и ее производные до n-го порядка включительно и записывают 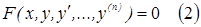 . Решение дифференциального уравнения называют такую функцию
. Решение дифференциального уравнения называют такую функцию 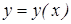 которая будучи подставлена в дифференциальное уравнение (1) обращает его в тождество. Если дифференциальное уравнение (1) можно разрешить относительно производной
которая будучи подставлена в дифференциальное уравнение (1) обращает его в тождество. Если дифференциальное уравнение (1) можно разрешить относительно производной 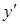 то его называют дифференциальным уравнением первого порядка разрешенным относительно производной и записывают
то его называют дифференциальным уравнением первого порядка разрешенным относительно производной и записывают 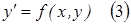 . Для уравнения (3) справедлива теорема о существовании и единственности его решения: Если для дифференциального уравнения
. Для уравнения (3) справедлива теорема о существовании и единственности его решения: Если для дифференциального уравнения 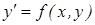 функция
функция 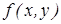 и ее частная производная определены и непрерывны в некоторой области D на плоскости ОХY содержащей некоторую точку с координаты
и ее частная производная определены и непрерывны в некоторой области D на плоскости ОХY содержащей некоторую точку с координаты 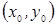 , то существует и притом единственное решения дифференциального уравнения
, то существует и притом единственное решения дифференциального уравнения 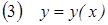 удовлетворяющая условию
удовлетворяющая условию 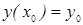 при этом условие
при этом условие 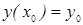 называется начальным условием для дифференциального уравнения (3). Геометрический смысл начального условия: Если y=y(x) решение дифференциального уравнения, то кривая описывающая этим решение проходит через точку (x0,y0=y(x0)). Функция
называется начальным условием для дифференциального уравнения (3). Геометрический смысл начального условия: Если y=y(x) решение дифференциального уравнения, то кривая описывающая этим решение проходит через точку (x0,y0=y(x0)). Функция 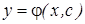 называют общим решением дифференциального уравнения (3) если: 1. она удовлетворяет при любом с дифференциального уравнения (3). 2. для данного начального условия
называют общим решением дифференциального уравнения (3) если: 1. она удовлетворяет при любом с дифференциального уравнения (3). 2. для данного начального условия 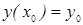 существует такое значение с=с0, что
существует такое значение с=с0, что 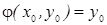 . Общим интегралом дифференциального уравнения (3) называют общее решение задаваемое не явно в виде уравнения
. Общим интегралом дифференциального уравнения (3) называют общее решение задаваемое не явно в виде уравнения 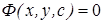 в частности общее решение
в частности общее решение 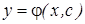 можно записать в виде общего интеграла
можно записать в виде общего интеграла 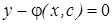 . Частым решение называют общее решение при частном значении параметра с=с0 т. е.
. Частым решение называют общее решение при частном значении параметра с=с0 т. е. 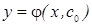 - частное решение. Частный интеграл это общий интеграл при частном значении с=с0 т. е.
- частное решение. Частный интеграл это общий интеграл при частном значении с=с0 т. е. 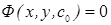 частный интеграл. Геометрический смысл общего решения (общего интеграла): общее решения
частный интеграл. Геометрический смысл общего решения (общего интеграла): общее решения 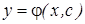 дифференциального уравнения (3) описывает семейство кривых на плоскости ОХY . Аналогично общий интеграл – семейство кривых на плоскости OXY. Частный интеграл (частное решение) описывает ту кривую на плоскости OXY из семейства кривых, которая проходит через точку с координаты
дифференциального уравнения (3) описывает семейство кривых на плоскости ОХY . Аналогично общий интеграл – семейство кривых на плоскости OXY. Частный интеграл (частное решение) описывает ту кривую на плоскости OXY из семейства кривых, которая проходит через точку с координаты 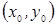 . Решить дифференциальное уравнение это значит: 1. найти его общее решение (или общий интеграл). 2. найти частное решение (или частный интеграл) если заданно начальное условие. В этом случае говорят – решить задачу Коши.
. Решить дифференциальное уравнение это значит: 1. найти его общее решение (или общий интеграл). 2. найти частное решение (или частный интеграл) если заданно начальное условие. В этом случае говорят – решить задачу Коши.
