Локальная формула муавра-лапласа

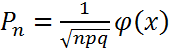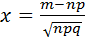, где , а 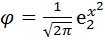– функция Гаусса, для кот имеются таблицы.

ИНТЕГРАЛЬНАЯ ФОРМУЛА МУАВРА-ЛАПЛАСА.

,

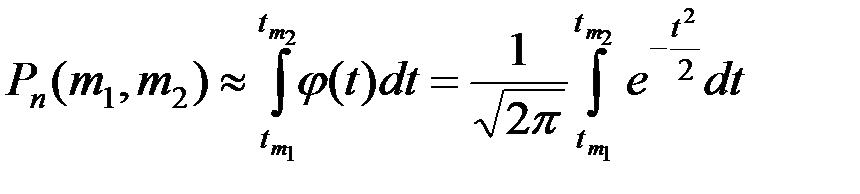где , .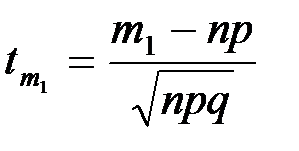

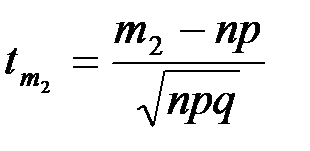СЛУЧАЙНАЯ ВЕЛИЧИНА.

Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.

Случайная величина обычно обозначается прописной латинской буквой ( 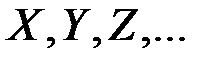), ее конкретные значения – строчными буквами ( ).

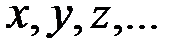Случайной величиной называется функция 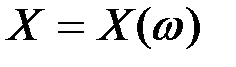, определенная на множестве элементарных событий , .

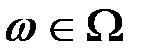Случайные величины делятся на дискретные и непрерывные.

Величина называется дискретной, если она может принимать определенные, фиксированные значения.

Случайная величина называется непрерывной, если она может принимать значения, сколь угодно мало отличающиеся друг от друга.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ЕЕ СВ-ВА

Свойства функции распределения

1. Функция распределения принимает значения из промежутка : .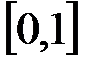

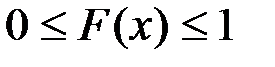2. Вероятность того, что случайная величина примет значение из полуинтервала 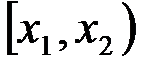, равна разности : .

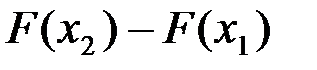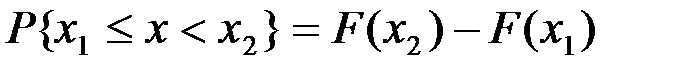3. Функция распределения – неубывающая функция, т.е. 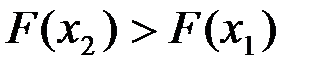при .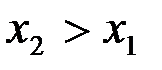

4. .

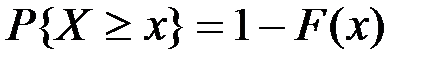5. Если 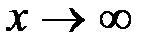, то .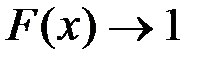

6. Если 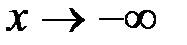, то .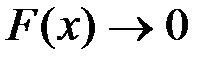

ОПР: функция распред-я любой дискрет-й случ величины есть разрывчатая ступенчатая функция, скачки которой происходят в точках соотв. возм-х значениям случ величины и равны вероят-м этих значений.

Дискретно распределенная случайная величина

ОПР: Математическое ожидание дискретной случайной величины – это сумма парных произведений всех возможных ее значений на соответствующие вероятности:

,

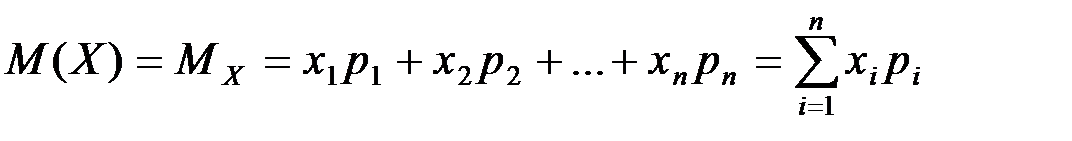где .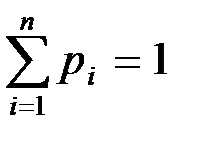

Свойства математического ожидания

1. Математическое ожидание постоянной величины 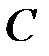равно этой величине.

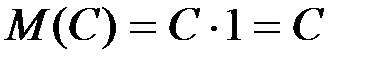
2. M(CX)= C·M(X)

3. M(X+Y)=M(X)+M(Y)

4.

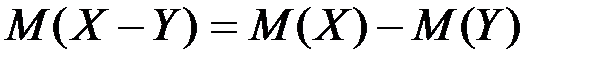
5.

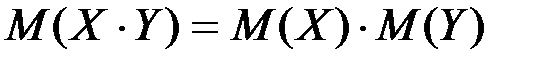
ОПР: Дисперсией случайной величины 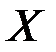называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания:

.

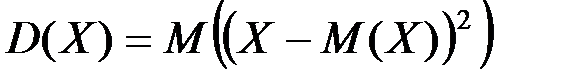Свойства дисперсии

1. Дисперсия постоянной величины равна нулю.

2.

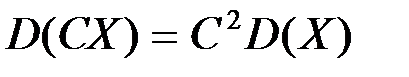
3.

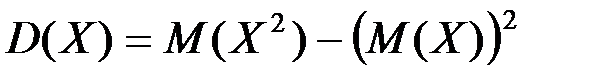
4.

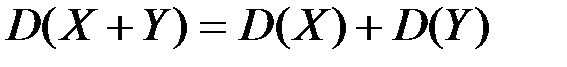
5. D(X-Y)= D(X)-D(Y)

ОПР: Средним квадратичным отклонением (или стандартом) случайной величины 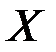называется корень квадратный из дисперсии 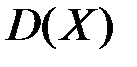этой величины: .

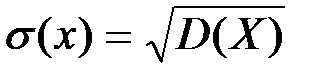НЕПРЕРЫВНО РАСПРЕДЕЛЕННАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА.

Математическим ожиданием непрерывной случайной величины 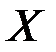называется значение интеграла:

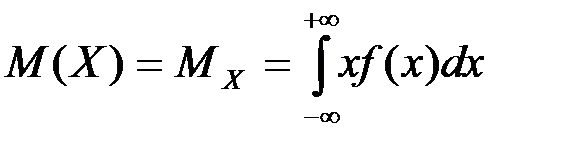
Дисперсией непрерывной случайной величины 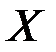называется значение интеграла:

.

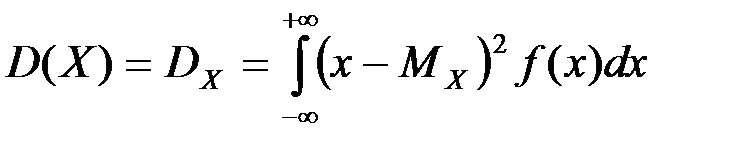Среднее квадратичное отклонениенепрерывной случайной величины 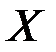вычисляется как корень квадратный из дисперсии:

.
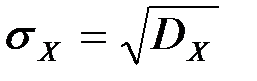