Уравнение прямой на плоскости

а) Каноническое уравнение прямой на плоскости имеет вид 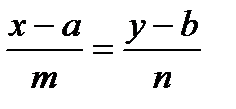, где точка 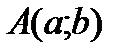лежит на прямой, а вектор 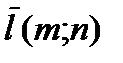является направляющим вектором прямой (он параллелен прямой).

б) Общее уравнение прямой на плоскости имеет вид 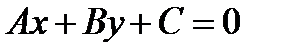. Легко видеть, что вектор 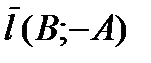является направляющим вектором прямой (он параллелен прямой). Вектор 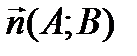называется нормалью к прямой (он перпендикулярен к прямой).

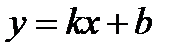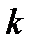в) Часто используется уравнение с угловым коэффициентом: , где равен тангенсу угла между данной прямой и осью ОХ.

Две прямые параллельны, если их направляющие векторы параллельны. Если две прямые перпендикулярны, то нормаль к одной из прямых является направляющим вектором другой прямой.

Пример.Написать уравнение плоскости P, проходящей через точку 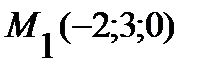перпендикулярно вектору 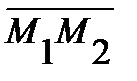, если .

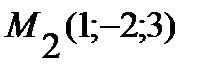Решение: а) Пусть 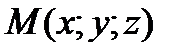– текущая точка плоскости P. Вывести уравнение плоскости – это значит записать аналитически условие, при котором произвольная точка (текущая точка) 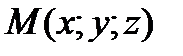будет принадлежать этой плоскости. Рассмотрим взаимное расположение произвольного вектора, принадлежащего плоскости 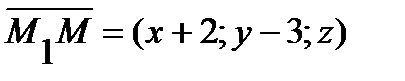и нормального вектора плоскости 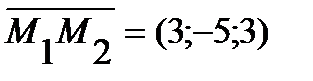. Очевидно, что точка 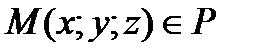, когда указанные векторы ортогональны. Условием ортогональности этих векторов является равенство нулю их скалярного произведения, т.е. 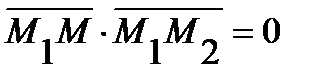. Записав это равенство через координаты векторов, получим уравнение искомой плоскост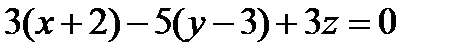и или .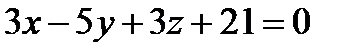

Пример. Найти угол между плоскостью P₁, проходящей через три точки 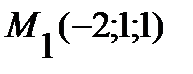, , 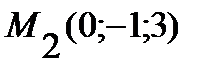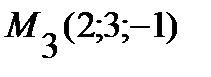и плоскостью P₂, заданной уравнением .

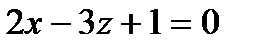Решение. Угол между плоскостями 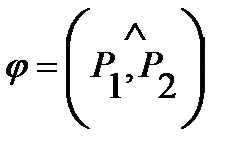равен углу между их нормальными векторами. Поэтому

.

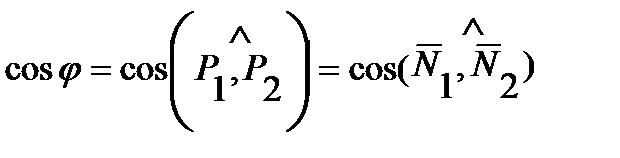Найдем нормальный вектор плоскости P₁ через векторы 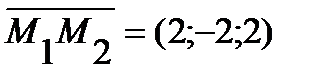, 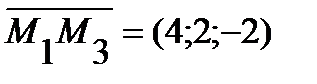. Очевидно, в качестве этого вектора можно взять вектор

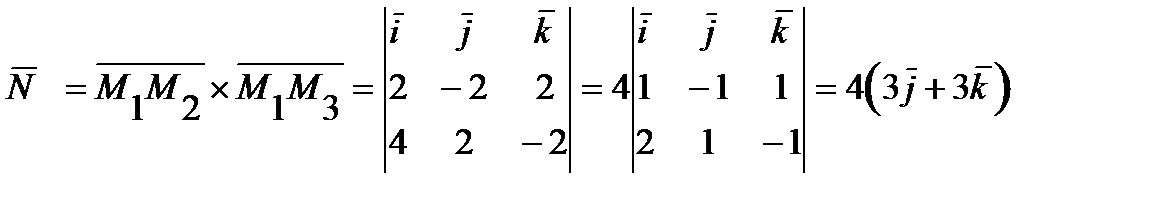
или ему коллинеарный вектор 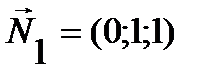. Нормальным вектором плоскости P₂ является вектор 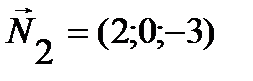. Угол между плоскостями определим из равенства

,

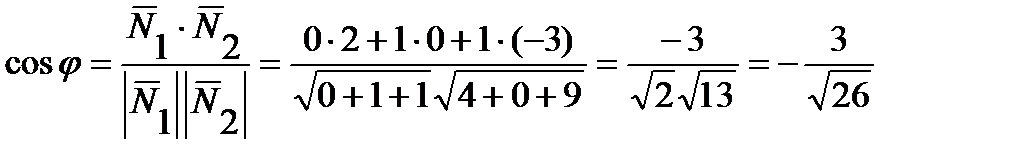откуда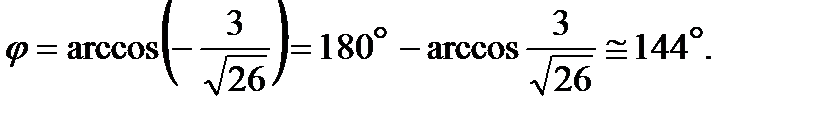

Пример. Прямая L задана общими уравнениями: 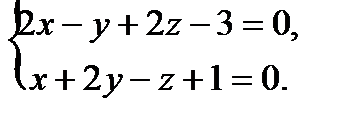Написать для этой прямой канонические, параметрические уравнения.

Решение. Выберем одну из точек, через которую пройдет указанная прямая, заданная пересечением плоскостей. Исходная система имеет бесчисленное множество решений, одно из которых получим придавая одной из переменных конкретное значение. Пусть 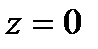, тогда значения других неизвестных находим из системы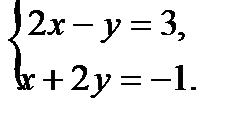

Решением этой системы является пара чисел .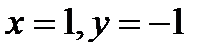

В результате получим точку 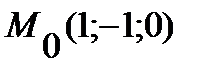, через которую проходит искомая прямая. В качастве направляющего вектора прямой можно взять вектор 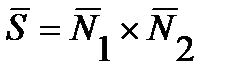, где 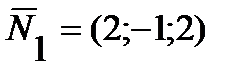, 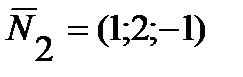- нормальные векторы плоскостей, линией пересечения которых является прямая. Таким образом,

.

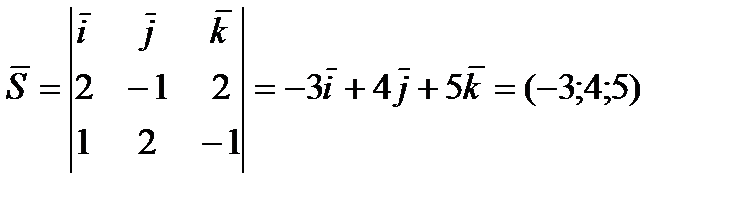Запишем канонические уравнения прямой: .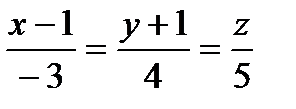

Обозначив равные отношения буквой t, получим параметрические уравнения прямой: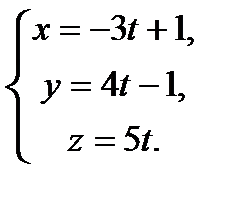

Пример.Даны вершины треугольника ABC: A(-4;2), B(8;-6), C(2;6).

Найти:

1) уравнение стороны AB;

2) уравнение высоты CH;

3) уравнение медианы AM;

4) точку N пересечения медианы AM и высоты CH;

5) уравнение прямой, проходящей через вершину C параллельно стороне AB.

Решение. 1) Используем уравнение прямой, проходящей через две точки A и B. Получим уравнение стороны AB: 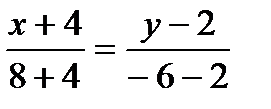, откуда 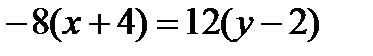или .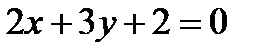

2) Высота опускается из точки C на сторону AB, угловой коэффициент которой 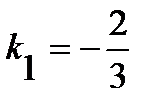. Если обозначим угловой коэффициент стороны CH через 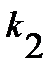, то согласно условию перпендикулярности 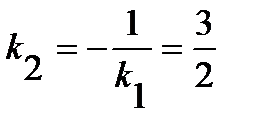. Воспользуемся уравнением пучка прямых, проходящих через точку C: 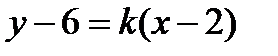. Из этого пучка выберем прямую, перпендикулярную AB, придав значение 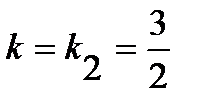. Получим 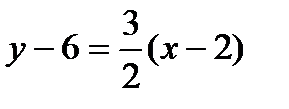или .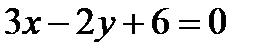

3) Предварительно найдем координаты середины М отрезка ВС: 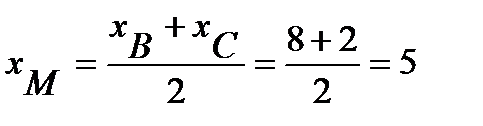, 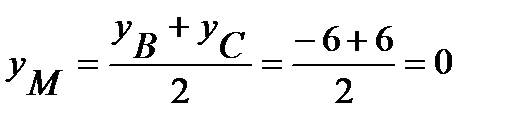. По известным двум точкам составляем уравнение прямой АМ:

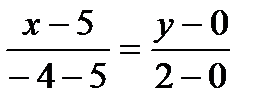или .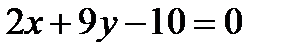

4) Точку пересечения N медианы АМ и высоты CH находим из совместного решения им соответствующих уравнений: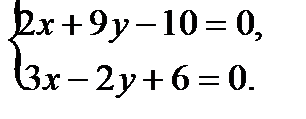

Решив эту систему, получим .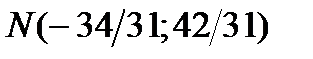

5) Воспользуемся уравнением пучка прямых, проходящих через точку С: 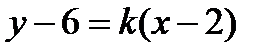. Выберем из него прямую, параллельную прямой AB, придав значение 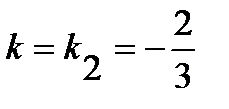. Получим уравнение искомой прямой в виде

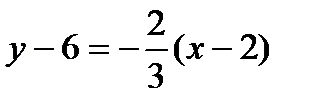или .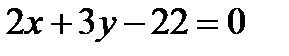

Задача. Даны координаты вершин пирамиды: 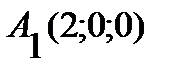, , 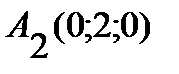, 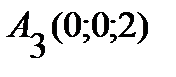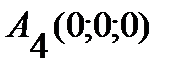. Найти: 1) длину ребра 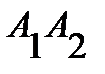; 2) угол между ребрам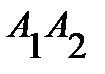и и 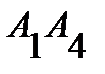; 3) угол между ребром 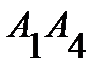и гранью 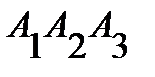; 4) площадь грани 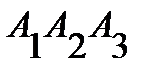; 5) объем пирамиды; 6) уравнение прямой 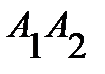; 7) уравнение плоскости 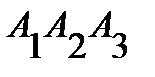; 8) уравнение высоты, опущенной на грань 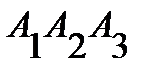(рис.1).

Рис.1

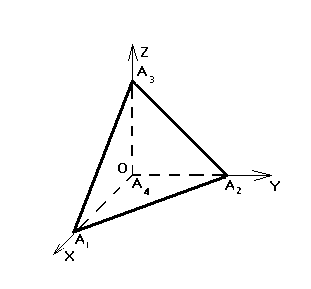
Решение: 1) длина ребра 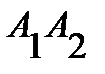есть длина вектора 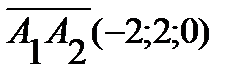. Следовательно, ;

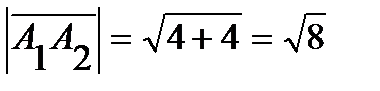2) угол между ребрам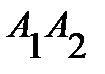и и 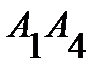есть угол между векторам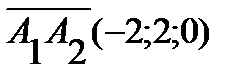и и 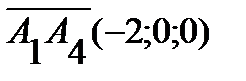. Поэтому

.

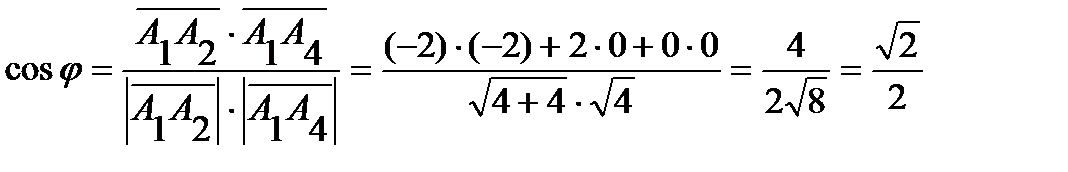Отсюда следует, что ;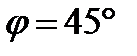

3) угол между гранью и ребром 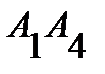есть угол между наклонной 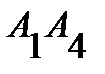и плоскостью, задаваемой точками 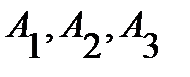. Из чертежа видно (рис.2), что 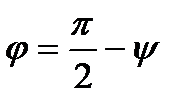, где 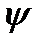- угол между вектором нормали 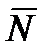плоскости 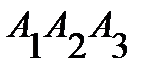и направляющим вектором 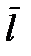прямой.

Так как по определению векторного произведения вектор 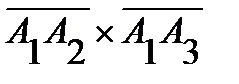перпендикулярен плоскости 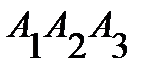, то его можно взять в качестве вектора нормали 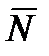. Итак, 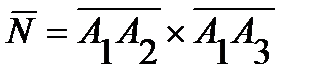. Найдем вектор :

.

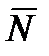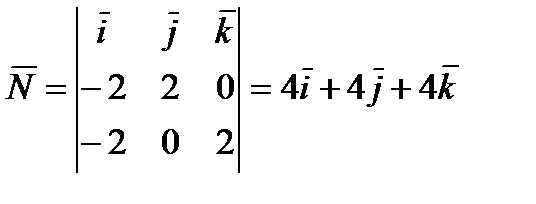Но тогда .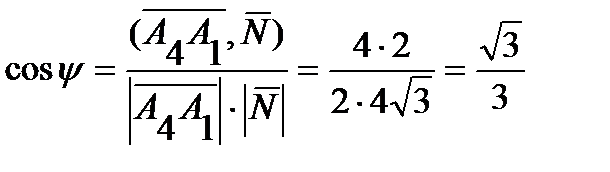

Отсюда .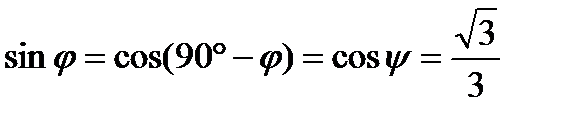

Искомый угол .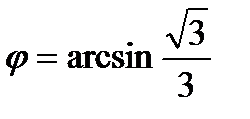

4) площадь грани ;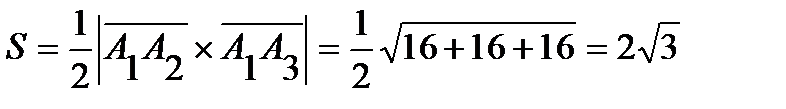

5) 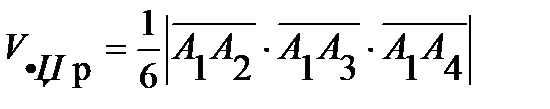. Но так как

,

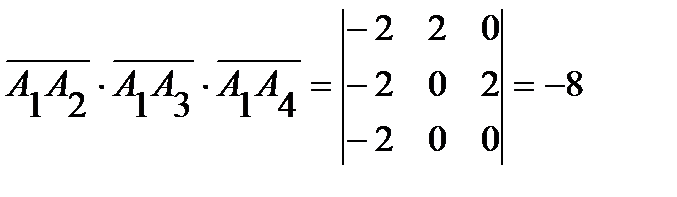то ;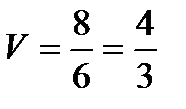

6) в качестве направляющего вектора прямой 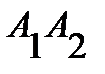можно взять 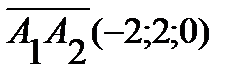. Поэтому уравнение прямой имеет вид

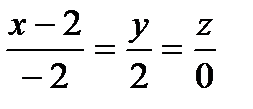или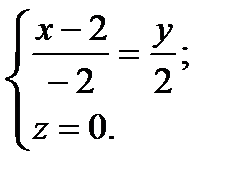

7) плоскость проходит через точку 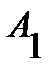перпендикулярно вектору 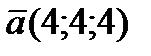. Поэтому уравнение грани 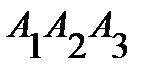имеет вид

.

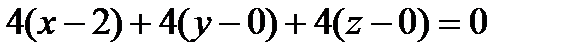Окончательно .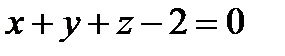

8) в качестве направляющего вектора высоты 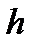можно взять вектор 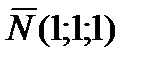нормали плоскости . Поэтому уравнение искомой высоты имеет вид

.
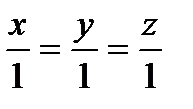