Способы описания и задания графов
1) Графический.
Данный способ задания подразумевает схематическое изображение графа на рисунке с указанием всех необходимых данных. В качестве примера можно привести
рис. 8.1 – 8.5.
2) Перечисление всех вершин и дуг.
Вершины: 1, 2, 3, 4, 5, 6.
Дуги: x1 <1, 2>, x2 <1, 3>, x3 <2, 5>, x4 <2, 4>, x5 <3, 6>, x6 <4, 6>, x7 <5, 6>.
3) Матрица смежности.
Если G=<V, X>, где V – совокупность вершин (n вершин), а X – совокупность дуг, то матрицей смежности этого графа называется квадратная матрица А(G) порядка n × n, где элемент матрицы либо 0, либо 1, в зависимости от того, смежны ли вершины.
A(G)=[ai j], где ai j =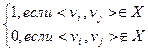 
Построим матрицу смежности для графа рис.8.5.
Таблица 8.1.
| A(G) | ||||||
4) Матрица инцидентности.
Если G=<V, X> – ориентированный граф, где V – совокупность вершин (n вершин), а X – совокупность дуг (m дуг), то матрицей инцидентности этого графа называется матрица B(G), размера n × m, где элемент матрицы либо 1, либо 0,
либо –1.
B(G)=[bi j], где bi j=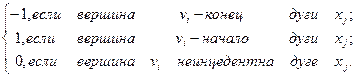 
Построим матрицу инцидентности для графа рис. 8.5.
Таблица 8.2.
| B(G) дуги вершины | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | -1 | -1 |
5) Матрица длин дуг.
Если G=<V, X> – ориентированный граф, где V – совокупность вершин (n вершин), а X – совокупность дуг, то матрицей длин дуг этого графа называется матрица С(G), размера n × n, где элемент матрицы это значения весовой функции для каждой из дуг или ребер.
С(G)=[сi j], где сi j=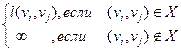 
Построим матрицу длин дуг для графа рис. 8.5.
Таблица 8.3.
| C(G) | ||||||
| ∞ | ∞ | ∞ | ∞ | |||
| ∞ | ∞ | ∞ | ∞ | |||
| ∞ | ∞ | ∞ | ∞ | ∞ | ||
| ∞ | ∞ | ∞ | ∞ | ∞ | ||
| ∞ | ∞ | ∞ | ∞ | ∞ | ||
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
Задача нахождения кратчайшего пути
Рассмотрим решение задачи нахождения кратчайшего пути методом «волны».
Пример
Допустим, в п. 1 находится склад, а в остальных пунктах – строительные площадки компании (рис. 8.6).
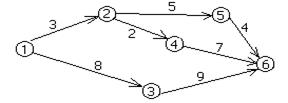Показатели на дугах – расстояния в километрах. Надо найти кратчайшие расстояния от склада до каждой строительной площадки.
Рис. 8.6.
Первый пункт является стартовым и ему присваивается постоянная метка.
Постоянная метка присваивается тем пунктам, если для них определено кратчайшее расстояние.
1) рассмотрим каждый пункт, в который можно попасть непосредственно из пункта 1.
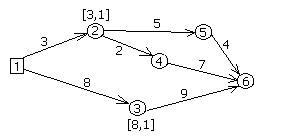До п. 2 расстояние в 3 км, до п. 3 – 8 км. Т.о. пунктам 2 и 3 присвоены временные метки [3,1] и [8,1] соответственно (рис. 8.7). Первое число в метке обозначает расстояние от п.1, второе число – это номер пункта, из которого непосредственно «пришли» в рассматриваемый пункт. Далее рассматриваются все временные метки на предмет нахождения метки с минимальным расстоянием. На данный момент это метка [3,1]. Пункту 2 присваиваем постоянную метку и фиксируем дугу из п.1 в п.2 (рис. 8.9).
Рис. 8.7
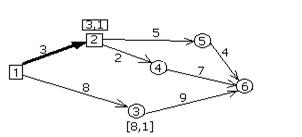
Рис. 8.9.
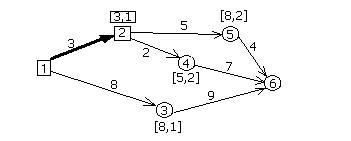2) теперь рассматриваются все пункты, которые ещё не имеют постоянных меток и непосредственно связаны с пунктом 2, т.е. мы рассматриваем п. 4 и п. 5. Достичь п. 4 можно, преодолев 3+2=5 км., а п. 5 – преодолев 3+5=8 км. Т.о. п. 4 и п. 5 присваиваются временные метки [5,2] и [8,2] соответственно (рис.8.10). Теперь снова рассматриваем временные метки и выбираем из них ту, которая имеет в своём обозначении кратчайшее расстояние, т.е. метку [5,2] для п.4. Эта метка теперь получает статус постоянной и фиксируем дугу из п.2 в п.4 (рис.8.11).
Рис. 8.10.
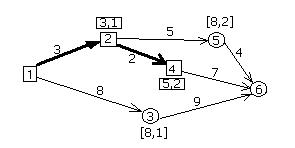
Рис. 8.11.
3) следующий этап начинается в п. 4, последнем, помеченном постоянной меткой. Как и раньше, рассматриваем каждый пункт без постоянной метки, в который можно попасть непосредственно из п. 4. В этом случае, это единственный п. 6. Для того, чтобы достичь
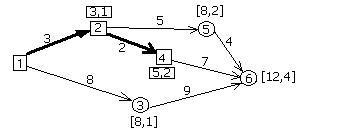п. 6 надо преодолеть 5+7=12 км.
Временная метка пункта 6 будет иметь вид [12,4] (рис. 8.12). Среди всех временных метках, которые имеются на данный момент, выбираем ту, которой соответствует наименьшее количество километров. Таких пунктов два: п. 5 и п. 3 ( до каждого из них длина равна 8 км.). Выбираем любой из этих пунктов, например, п. 5. Эта метка
Рис.8.12. фиксируется как и путь из п. 2 в п. 5 (рис. 8.13).
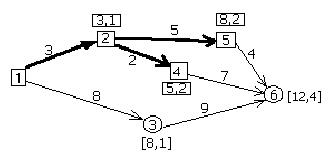
Рис. 8.13.
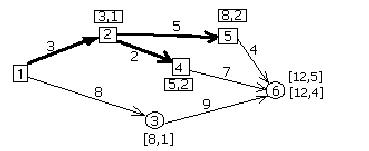4) теперь рассмотрим пункты, в которые можно попасть из п. 5. Таковым является только п. 6, имеющий уже временную метку. Добавляем к этой временной метке ещё одну, относящуюся к п. 5 (рис. 8.14).
Из имеющихся трёх временных меток опять выбираем ту, в которой указано минимальная длина пути от п. 1 до данного пункта. Таковой меткой является
Рис. 8.14 метка [8,1] для п. 3. Эти пункт и метка получают статус стационарных и путь из п. 1 в п. 3 фиксируется (рис. 8.15).
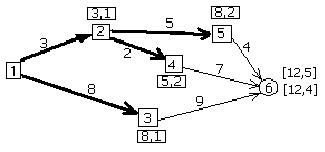
Рис. 8.15.
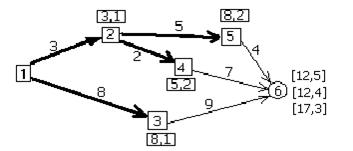5) из фиксированного п. 3 можно попасть в п. 6, у которого уже есть две временные метки, но нет постоянной. Добавляем п. 6 ещё одну временную метку [17,3] (рис. 8.16). Т. о. п. 6 имеет три временные метки, т. е. до п. 6 можно пройти тремя путями различной длины. Выбираем наикратчайший путь. Таких пути два: через п. 5 и через п. 6. Выбираем любой, потому что длина их одинаковая. Пусть это будет путь,
проходящий через п. 4. Тогда фиксируем
Рис. 8.16 метку [12,4], п. 6 и путь из п. 4 в п. 6 (рис.8.17).
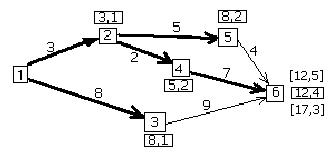
Рис. 8.17.
Теперь можно использовать информацию в постоянных метках для нахождения кратчайшего пути из п. 1 в любой другой пункт. Например, кратчайший путь из п. 1 в п. 4 есть путь 1 – 2 – 4 и длина его 5 км. Используя этот подход, можно определить кратчайшие пути применительно ко всей сети компании, состоящей из её строительных площадок.
Таблица 8.4.
| Пункт | Кратчайший путь из п.1 | Расстояние, км. |
| 1 – 2 1 – 3 1 – 2 – 4 1 – 2 – 5 1 – 2 – 4 – 6 |
Сетевой график
Сетевой график — это динамическая модель производственного процесса, отражающая технологическую зависимость и последовательность выполнения комплекса работ, увязывающая их свершение во времени с учетом затрат ресурсов и стоимости работ с выделением при этом узких (критических) мест.
Примером сетевого графика может быть граф, вершины которого отображают состояния некоторого объекта (например, строительства), а дуги — работы, ведущиеся на этом объекте. Каждой дуге сопоставляется время, за которое осуществляется работа и/или число рабочих, которые осуществляют работу. Часто сетевой график строится так, что расположение вершин по горизонтали соответствует времени достижения состояния, соответствующего заданной вершине.
Основными элементами сетевого графика являются: работа, события, пути.
Работа
Работа отражает трудовой процесс, в котором участвуют люди, машины, механизмы, материальные ресурсы (проектирование сооружения, поставки оборудования, кладка стен, решение задач на ЭВМ и т. п.) либо процесс ожидания (твердение бетона, сушка штукатурки и т. п.). Каждая работа сетевого графика имеет конкретное содержание.
Виды работ
· действительная работа в прямом смысле слова (например — подготовка трассы соревнований), требующая затрат труда, материальных ресурсов и времени;
· ожидание — работа не требующая затрат труда и материальных ресурсов, но занимающая некоторое время;
· фиктивная работа (зависимость) — связь между двумя или более событиями, не требующая затрат труда, материальных ресурсов и времени, но указывающая, что возможность начала одной операции непосредственно зависит от выполнения другой. Продолжительность такой работы = 0.
Фиктивные работы изображают штриховыми линиями в виде дополнительных дуг и используют для правильного и наглядного отображения порядка предшествования работ при построении сети.
Всякая работа в сети соединяет два события: предшествующее (являющееся для нее начальным) и следующее за ней (конечное).
Событие
Событие выражает факт окончания одной или нескольких непосредственно предшествующих (входящих в событие) работ, необходимых для начала непосредственно следующих (выходящих из события) работ. Событие, стоящее в начале работы, называется начальным, а в конце – конечным.
Виды событий
· исходное событие — начало выполнения комплекса работ;
· завершающее событие — конечное событие, означающее достижение конечной цели комплекса работ;
· промежуточное событие, как результат одной или нескольких работ, представляющих возможность начать одну или несколько непосредственно следующих работ. Продолжительность промежуточного события во времени всегда = 0.
В исходное событие сетевого графика не входит, а из завершающего не выходит ни одна работа. В отличие от работ, события совершаются мгновенно без потребления ресурсов.
Следует отметить, что событие определяет состояние, а не процесс.
Пути
Любая последовательность работ в сетевом графике, в котором конечное событие каждой работы этой последовательности совпадает с начальным событием следующей за ней работой, называется путем.
Виды пути
- полный путь — начало которого совпадает с исходным событием сети, а конец — с завершающим, называется полным путем;
- путь, предшествующий событию — путь от исходного события сети до данного события;
· путь, следующий за событием — путь, соединяющий событие с завершающим событием;
- путь между событиями i и j — путь, соединяющий какие-либо два события i и j, из которых ни одно не является исходным или завершающим событием сетевого графика;
- критический путь — путь, имеющий наибольшую продолжительность от исходного события до завершающего.
Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь наибольшей длины между исходными и завершающими событиями называется критическим (Lm).
Если критическое время не соответствует заданному или нормативному, сокращение сроков производственного процесса необходимо начинать с сокращения продолжительности критических работ.