Проводник в электрическом поле

Вещество или материальное тело, в котором имеются заряды, способные переносить электрический ток, называется проводником. В металлах переносчиками тока служат свободные (т.е. не привязанные к атомам) электроны, в электролитах — ионы, в плазме — и электроны, и ионы. Для электростатических явлений поле внутри проводника равно нулю:

E→in ≡ 0 .

Механизм исчезновения электрического поля в проводниках связан со смещением свободных зарядов ровно настолько, чтобы как раз компенсировать внешнее электрическое поле, если таковое имеется. При изменении внешнего поля свободные заряды в проводнике перераспределяются, а в момент перераспределения в проводнике течет ток. Пример такой компенсации внутри проводящей пластины изображен на рис. 1.25.

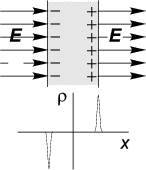
Рис. 1.25: Проводящая пластина в однородном электрическом поле и распределение плотности заряда в объёме проводника. В плазме толщина заряженного слоя на поверхности составляет несколько радиусов Дебая, в металле — несколько длин Ферми.

Поскольку E→in = 0, то и плотность заряда внутри проводника также равна нулю:

ρin = 1 4π divE→in ≡ 0.

Заряды, компенсирующие внешнее поле, могут размещаться только на поверхности проводника. В связи с этим говорят, что проводник квазинейтрален. По аналогии с объёмной плотностью заряда ρ = limΔV →0Δq∕ΔV , поверхностную плотность определяют, как предел отношения заряда на физически малом участке поверхности Δq к площади этого участка ΔS:

σ = limΔS→0Δq∕ΔS .

Все точки проводника имеют одинаковый потенциал, так как gradϕin = −E→in = 0. Поверхность проводника также эквипотенциальна. Следовательно, электрическое поле перпендикулярно к ней. Этот факт иногда формулируют в виде равенства нулю тангенциальной (касательной к поверхности проводника) проекции внешнего электрического поля E→t = [[n→,E→],n→]:

E→t = 0.

Здесь и далее n→ обозначает внешнюю нормаль к поверхности проводника.

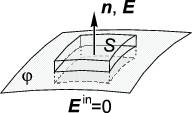
Рис. 1.26: Поток через верхнюю грань параллелепипеда, натянутого на элемент поверхности S, равен En S; поток через остальные грани равен нулю. Сравнивая En S с полным зарядом 4π σ S внутри параллелепипеда, получаем граничное условие En = 4πσ.

Нормальная компонента электрического поля на поверхности проводника En = (n→,E→) однозначно связана с поверхностной плотностью зарядов. Применяя теорему Гаусса к параллелепипеду, натянутому на элемент поверхности проводника (рис. 1.26), получаем:

E→n = 4πσ .

Обычно распределение зарядов σ по поверхности проводника неизвестно. Если нужно, его находят в результате решения задачи (см. след. параграф). Однако одну существенную закономерность можно указать из качественных соображений (Б.Франклин, 1747 г.). Так как одноименные заряды (заряды одного знака) отталкиваются, они стремятся разойтись в проводнике как можно дальше. Это приводит к накоплению зарядов на наиболее удаленных участках проводников, например на остриях. Поле вблизи острия можно приближенно представить, как поле заряженной сферы того же радиуса кривизны r. Отсюда можно оценить напряженность электрического поля и поверхностную плотность заряда 4πσ ∼ E ∼ ϕ∕r, где ϕ — потенциал проводника относительно соседних тел. При этом полезно отметить, что полный заряд острия q ∼ πr2σ ∼ ϕr все-таки составляет малую долю заряда всего проводящего тела Q ∼ ϕR, где R — его характерный размер.

Уравнение Лапласа.

При наличии проводников общее решение уравнения Пуассона (10.1) для электростатического потенциала можно представить в виде, явно учитывающем поверхностные заряды на их поверхности: ϕ(r→) = ∫ V ρ(r′→)dV ′ ∣r→ −r′→∣ + ∫ Sσ(r′→)dS′ ∣r→ −r′→∣. (13.1)

Формула (13.1) получается из (11.2), если объемную плотность зарядов в проводниках выразить через поверхностную плотность заряда σ с помощью одномерной δ-функции ρ(z) = σ δ(z), где координата z отсчитывается от поверхности проводника по нормали к ней, а также учесть, что dV = dS dz.

Однако поверхностная плотность σ обычно не известна, а сама зависит от электрического поля (от потенциалов всех проводников). Поэтому формальное решение уравнения Пуассона (13.1) по сути дела само является уравнением, но не дифференциальным, а интегральным, так как неизвестное поле входит под знаком интеграла через граничное условие σ = En∕4π.

Чтобы не заниматься решением интегрального уравнения, можно в уравнении Пуассона учитывать только плотность зарядов вне проводников (эти заряды обычно «закреплены» и поэтому известны), а вместо σ задать потенциалы проводников. Иными словами, нужно решать уравнение Пуассона при дополнительных граничных условиях ϕ(r) ∣Sj = ϕj (13.2)

на поверхности Sj проводников. Иногда бывают фиксированы на потенциалы, а заряды проводников. В этом случае говорят, что потенциалы проводников ϕj «плавают», но всё равно они постоянны на поверхности каждого проводника. Тогда решают задачу, задав некоторый набор констант ϕj, а после того как поле найдено, подгоняют эти константы так, чтобы выполнялись дополнительные условия 1 4π ∮ Sj(E→,dS→) = qj. (13.3)

Встречаются также смешанные постановки задачи, когда для одних проводников заданы потенциалы, а для других — заряды.

Простейшим, но практически очень важным является случай полного отсутствия внешних зарядов, так что ρ = 0. Тогда нужно решать уравнение Лапласа Δϕ = 0 (13.4)

с граничными условиями (13.2) или (13.3). Уравнение Лапласа относится к классу уравнений в частных производных второго порядка. Только в редких ситуациях, когда потенциал зависит лишь от одной пространственной координаты, оно превращается в обыкновенное дифференциальное уравнение. Разработаны изощренные методы решения уравнения Лапласа, которые изучают в курсе математической физики. На простейших примерах некоторые из них изложены в приложении к данному параграфу.

Математики прилагают немало усилий для доказательства единственности решения того или иного уравнения. Физики зачастую считают единственность решения тривиальным фактом. Между тем известно немало систем, которые при одинаковых условиях могут находится в разных состояниях.Уравнение Пуассона с нелинейной правой частью, когда ρ зависит от ϕ, также может иметь решения типа гистерезиса.1 Поэтому мы всё-таки потратим некоторое время, чтобы доказать единственность решения уравнения Лапласа.

Предположим обратное. Пусть ϕ и ϕ̃ — два различных решения уравнения Лапласа или уравнения Пуассона с фиксированной правой частью (т.е. плотность зарядов ρ вне проводников не зависит от электрического поля). Разность этих решений

χ = ϕ −ϕ̃

удовлетворяет уравнению Лапласа

Δχ = 0.

На поверхности проводников с фиксированным потенциалом

χ ∣S = 0,

а на поверхности проводников с плавающим потенциалом

∮ S(∇χ,dS→) = 0,χ ∣S = const .

Воспользуемся теоремой Остроградского–Гаусса

∫ V diva→dV = ∮ S(a→,dS→),

записав её для вектора a→ = gradχ2∕2 = χgradχ:

∫ V div(χgradχ)dV = ∮ S(χgradχ,dS→).

Интеграл в правой части по поверхности проводников равен нулю в силу граничных условий. Подынтегральное выражение в левой части преобразуем с помощью тождества

div(χgradχ) = (gradχ)2 + χdivgradχ.

Так как divgradχ = Δχ = 0 из теоремы Остроградского–Гаусса получаем интегральное уравнение

∫ V (gradχ)2 dV = 0.

Поскольку под знаком интеграла здесь стоит неотрицательная величина (gradχ)2, равенство нулю всего интеграла возможно только при условии, что всюду gradχ = 0. Таким образом, два решения ϕ и ϕ̃ если и различаются, то только на несущественную аддитивную константу. Впрочем, если потенциал хотя бы одного проводника фиксирован, то эта константа с необходимостью равна нулю. Тем самым единственность решения доказана.

Теорема единственности оправдывает использование эвристического подхода к решению задач электростатики. Если решение угадано, то не нужно искать другие решения. Мы воспользуемся этим фактом в следующем параграфе.