Срок сдачи курсовой работы: 02.12.2014г

Курсовая работа по математической логике

ТЕМА: Предикаты и их применение

Цель:Научиться применять предикаты для формализации задачи и уметь определять истинность предикатов на различных множествах.

Задания: 1.В соответствии с вариантом, выполнить задания (к главе 2).

2. Введя соответствующие предикаты, записать на языке логики предикатов какое-либо утверждение (регламент, статья какого-либо закона) из учебника Белов Е.Б, Лось В.П. и др. «Основы информационной безопасности», (возможно выполнение группами численностью не более 3-х человек) (к главе 3)

3. Придумать и сформулировать задачу, относящуюся к специальности, решение которой возможно с помощью логики предикатов (возможно выполнение группами численностью не более 3-х человек) (к главе 3).

Оформление: Работа выполняется на листах формата А4.

Цель работы: расширить знания о методах и способах решения логических задач

Требования к курсовой работе:

1. Курсовая работа выполняется по следующему плану:

1) Титульный лист;

2) Содержание;

3) Пояснительная записка;

4) Глава 1. Основные понятия алгебры предикатов.

5) Глава 2. Предикат и его область истинности.

6) Глава 3. Применение предикатов.

7) Заключение;

8) Список используемой литературы.

2. Пояснительная записка содержит краткое пояснение к каждой из глав курсовой работы.

3. Первая глава содержит основные понятия и определения теории предикатов.

4. Вторая глава содержит решение задач с пояснениями.

5. Третья глава содержит словесную формулировку выбранного утверждения, его формализацию в виде предиката, соответствующую базу данных. На защиту предоставляется презентация по 3-й главе.

6. Оформление: объем работы – не менее 15 страниц; работа сдается на проверку в распечатанном виде (формат А4; шрифт Arial, 14; левое поле – 2,5, остальные поля – 1,5; красная строка - 0,75, полуторный интервал, выравнивание по ширине; нумерация страниц).

Срок сдачи курсовой работы: 02.12.2014г.

Литература:

1. Верещагин Н. К., Шень А. «Лекции по математической логике и теории алгоритмов. Часть 2. Языки и исчисления»
2. Пономарев В.Ф. «Дискретная математика для инженеров»
3. Белов Е.Б, Лось В.П. и др. «Основы информационной безопасности»

Таблица для определения вариантов

№ варианта	Порядковые номера заданий для п.1.
	1.1	3.1	5.1	7.1		11.1	12.1
	1.2	3.2	5.2	7.2	10.1	11.2	12.2
	1.3	4.1	5.3	7.3	10.2	11.3	12.3
	1.4	4.2	5.4	7.4	10.3	11.4	12.4
	1.5	4.3	6.1	7.5	10.4	11.5	13.1
	1.6	4.4	6.2		10.5	11.1	13.2
	1.7	3.1	6.3	7.1	10.6	11.2	13.3
	1.8	3.2	6.4	7.2	10.7	11.3	13.4
	2.1	4.1	6.5	7.3	10.8	11.4	13.5
	2.2	4.2	6.6	7.4	10.9	11.5	13.6
	2.3	4.3	6.7	7.5		11.1	13.7
	2.4	4.4	6.8		10.1	11.2	13.8
	2.5	3.1	6.9	7.1	10.2	11.3	13.9
	2.6	3.2	6.10	7.2	10.3	11.4	12.1
	2.7	4.1	6.11	7.3	10.4	11.5	12.2
	2.8	4.2	6.12	7.4	10.5	11.1	12.3
	2.9	4.3	6.13	7.5	10.6	11.2	12.4
	2.10	4.4	6.14		10.7	11.3	13.1
	2.11	3.1	6.15	7.1	10.8	11.4	13.2
	2.1	3.2	6.16	7.2	10.9	11.5	13.3
	2.2	4.1	6.17	7.3		11.1	13.4
	2.3	4.2	6.18	7.4	10.1	11.2	13.5
	2.4	4.3	6.19	7.5	10.2	11.3	13.6
	2.5	4.4	6.20		10.3	11.4	13.7
	2.6	3.1	5.1	7.1	10.4	11.5	13.8
	2.7	3.2	5.2	7.2	10.5	11.1	13.9
	2.8	4.1	5.3	7.3	10.6	11.2	12.1
	2.9	4.2	5.4	7.4	10.7	11.3	12.2
	2.10	4.3	6.1	7.5	10.8	11.4	12.3
	2.11	4.4	6.2		10.9	11.5	12.4

Задание 1. Среди следующих предложений выделить предикаты и для каждого из них указать область истинности, если М = R для одноместных предикатов и М = R х R для двухместных предикатов:

1) х + 5 = 1;

2) при х = 2 выполняется равенство ;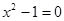

3) ;

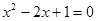4) существует такое число х, что ;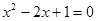

5) х + 2 < 3х-4;

6) однозначное число х кратно 3;

7) (х+2)-(3х-4);

8) .

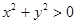Задание 2. Среди следующих предложений выделите предикаты, для каждого из предикатов укажите одну из возможных областей определения и в соответствии с ней область истинности:

1) Луна есть спутник Венеры;

2) Планеты х и у принадлежат Солнечной системе;

3) ;

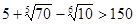4) ;

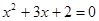5) ;

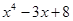6) Любое простое число р не имеет делителей, отличных от себя и 1;

7) Натуральное число n не меньше 1;

8) Треугольник АВС равен треугольнику А₁В₁С₁;

9) х² + 2х + 1 > 0;

10) ;

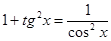11) .

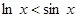Задание 3. Даны предикаты Р(х): «х²- 4 = 0» и Q(x): «3х- 2 < 17». Найдите области истинности этих предикатов, если их область определения есть: 1) R; 2) N.

Задание 4. Найти области истинности предикатов:

1) ;

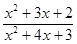2) ;

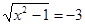3) ;

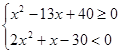4) .

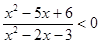Задание 5. Пусть даны предикаты: Р(х): «Х четное число» и Q(X): «Х кратно 3», определенные на множестве N. Найти области истинности предикатов:

1) p(x)&Q(x).

2) p(x)ÚQ(x).

3) ØР(х).

4) р(х)→ Q(x).

Задание 6. На множестве М = {l, 2, 3,...,20} заданы предикаты:

А(х): «x не делится на 5»;

В(х): «х - четное число»;

С(х): «х - число простое»;

D(х): «х кратно 3».

Найдите множества истинности следующих предикатов:

1) А(х)ÙВ(х);

2) С(х) ÙВ(х);

З) C(x) ÙD(x);

4) B(x) ÙD(x);

5) ØB(x) ÙD(x);

6) A(x) Ù ØD(x);

7) ØB(x) Ù ØD(x);

8) A(x) ÙB(x) ÙD(x);

9) А(х) ÚВ(х);

10) В(х) ÚС(х);

11) C(x) ÚD(x);

12) B(x) ÚD(x);

13) ØВ( х)Ú D(x);

14) В(х)ÚØD(x);

15) А(х) ÚВ(х) ÚD(x);

16) С(х) → А(х);

17) D(x) →ØС(х);

18) А(х) →В(х);

19) (A(x) ÙC(x))→ØD(х);

20) (A(x) ÙD(x))→ØС(х).

Задание 7. Изобразите на диаграммах Эйлера-Венна области истинности для следующих предикатов:

1) ØP(x)ÙØQ(x);

2) ØР(х) « Ø Q(x);

3) (Р(х→Q(х))ÚR(x)ÙØQ( x);

4) Р(х)→(Q(х)ÚØQ( x));

5) Р(x)ÙQ(х)→ØR(х).

Задание 8. Пусть даны предикаты А(х,у) и B(x,y), определенные на множестве М =М₁хМ₂ Ì RхR. Найти множество истинности предиката А(х, у)«В(х, у) и изобразить ее с помощью кругов Эйлера-Венна.

Задание 9. Записать предикат, полученный в результате логических операций над предикатами Р(x), Q(x) и R(x) , область истинности которого заштрихована на рисунке.

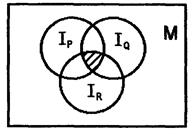
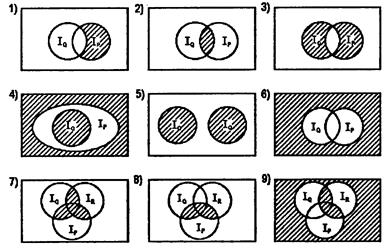
Задание 10. Записать предикаты, полученныe в результате логических операций над предикатами Р(х), Q(x) и R(х), области истинности которых (I) заштрихованы на следующих рисунках:

Задание 11. Выяснить, какие из следующих предикатов являются тождественно истинными:

1) ;

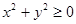2) ;

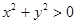3) ;

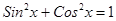4) ;

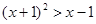5) .

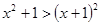Задание 12. Даны предикаты Р(х): х² + х + 1 >0 и Q(х): х²- 4х + 3 = 0 , определенные на множестве R. Требуется установить, какие из следующих высказываний истинны и какие ложны:

1) "x Р(х);

2) $х Р(х);

3) "x Q(х);

4) $х Q(х).

Задание 13. Установить, какие из следующих высказываний истинны, а какие ложны, при условии, что область определения предикатов М совпадает с R:

1) $х (х + 5 = х + 3);

2) $х (х² +х +1/2 =0);

3) "х (х² +х + 1 >0);

4) "х (х²-5х + 6³0);

5) $х ((х²-5х + 6³0)Ù(х²-2х + 1>0));

6) $х ((х^2-5х + 6³0) Ù (х²-6х + 8≤0));

7) "х ((х²-6х + 8³0)Ú(х²-6х + 8<0));

8) $х ((хÎ{2, 5})→(х²-6х + 8 =0));

9) "х ((хÎ{3, 5})→(х²-6х + 8 < 0)).