Для очно заочной формы обучения
Семинар 1 (тема 1)
1. Повторение материала темы.
2. Заданы матрицы A и B

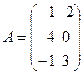 ,
, 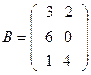
Указать, какие операции над матрицами выполнимы, и осуществить эти операции:
а) 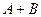 ; б)
; б) 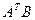 ; в)
; в) 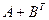 ; г)
; г) 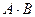 ; д)
; д) 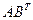 ; е)
; е) 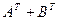 ; ж)
; ж) 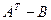 ; з)
; з) 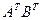 ;
;
k) Найти матрицу C= 6A-3B и матрицу 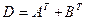 ;.
;.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 2 (тема 1)
1. Задана матрица
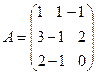
Найти матрицы 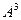 и
и 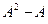
2. Вычислить определители матриц
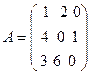 ,
, 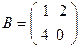 ,
, 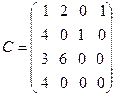
*Примечание: занятие проводится в форме исследования с образованием несколько подгрупп для решения задач по тематике занятия; коллективный обмен результатами работы и анализ выявленных типичных ошибок.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 3 (тема 1)
1. Решить уравнения
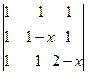 =0,
=0, 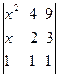 =0.
=0.
2. Найти ранги матриц
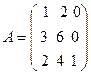 ,
, 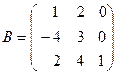 ,
, 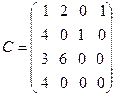 .
.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 4 (тема 2)
1. Повторение материала темы.
2. Решить систему уравнений по формулам Крамера
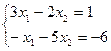 ,
, 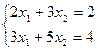 .
. 
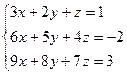
*Примечание: занятие проводится в форме исследования с образованием несколько подгрупп для решения задач по тематике занятия; коллективный обмен результатами работы и анализ выявленных типичных ошибок.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 5 (тема 2)
Записать систему уравнений из Семинара 7 в матричном виде и решить ее как матричное уравнение.
*Примечание: занятие проводится в форме исследования с образованием несколько подгрупп для решения задач по тематике занятия; коллективный обмен результатами работы и анализ выявленных типичных ошибок.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 6 (тема 2)
Решить систему уравнений методом Гаусса
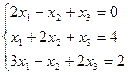
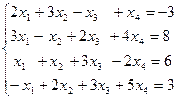
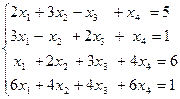
*Примечание: занятие проводится в форме исследования с образованием несколько подгрупп для решения задач по тематике занятия; коллективный обмен результатами работы и анализ выявленных типичных ошибок.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 7 (тема 3)
1. Повторение материала темы.
2. Является ли система векторов 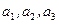 линейно независимой
линейно независимой
а) 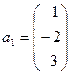 ,
, 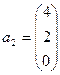 ,
, 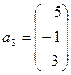 ; б)
; б) 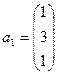 ,
, 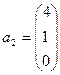 ,
, 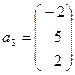 .
.
Если система векторов 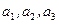 является линейно независимой, то выразить нижеприведенный вектор
является линейно независимой, то выразить нижеприведенный вектор 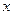 в базисе данных векторов
в базисе данных векторов
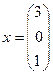 .
.
3. Найти матрицу линейного преобразования, переводящего каждый вектор 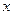 трехмерного линейного пространства в вектор
трехмерного линейного пространства в вектор 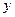 , причем
, причем
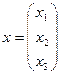 ,
, 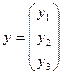 .
.
а) 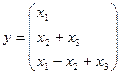 , б)
, б) 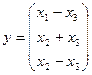 .
.
4. Найти матрицу линейного преобразования, переводящего каждый вектор 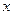 двумерного линейного пространства в вектор
двумерного линейного пространства в вектор 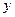 по следующему правилу:
по следующему правилу:
а) Симметричное отображение относительно прямой 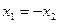 .
.
б) Симметричное отображение относительно прямой 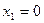 , а затем симметричное отображение относительно начала координат.
, а затем симметричное отображение относительно начала координат.
в) Удвоение значения первой координаты, а затем симметричное отображение относительно прямой 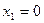 .
.
г) Симметричное отображение относительно прямой 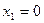 , а затем симметричное отображение относительно прямой
, а затем симметричное отображение относительно прямой 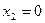 .
.
*Примечание: занятие проводится в форме организационно-деятельностной игры с разбиением группы на подгруппы и постановкой для 2-3-х подгрупп одинаковой задачи с последующим выбором в ходе коллективного обсуждения оптимального способа решения.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 8 (тема 3)
1. Определить косинус угла между векторами 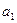 и
и 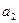 , принадлежащими трехмерному евклидову пространству с ортонормированным базисом
, принадлежащими трехмерному евклидову пространству с ортонормированным базисом
а) 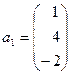 ,
, 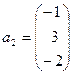 ; б)
; б) 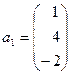 ,
, 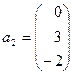 .
.
2. Написать уравнения касательных к параболе 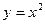 , проходящих через заданную точку плоскости
, проходящих через заданную точку плоскости 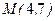 . Составить уравнения нормалей к касательным, построенных в указанной точке
. Составить уравнения нормалей к касательным, построенных в указанной точке 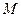 .
.
3. Дана прямая 2x+5y-1=0. Составить уравнение прямой, проходящей через точку M(-1,3) : а)параллельно данной прямой; б) перпендикулярно данной прямой.
4. Через вершины треугольника А(-1,2), В(3,-1) и С(0,4) проведены прямые параллельно противолежащим сторонам. Составить их уравнения.
*Примечание: занятие проводится в форме организационно-деятельностной игры с разбиением группы на подгруппы и постановкой для 2-3-х подгрупп одинаковой задачи с последующим выбором в ходе коллективного обсуждения оптимального способа решения.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 9 (тема 4)
1. Повторение материала темы.
2. Заданы комплексные числа
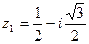 и
и 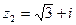 .
.
а) Найти и изобразить на комплексной плоскости числа
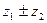 ,
, 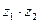 ,
, 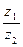 .
.
б) Записать комплексные числа в тригонометрической и экспоненциальной формах.
Найти и изобразить на комплексной плоскости числа
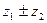 ,
, 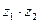 ,
, 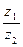 ,
, 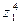 ,
, 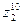 ,
, 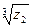 .
.
*Примечание: занятие проводится в форме организационно-деятельностной игры с разбиением группы на подгруппы и постановкой для 2-3-х подгрупп одинаковой задачи с последующим выбором в ходе коллективного обсуждения оптимального способа решения.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 10 (тема 5)
1. Повторение материала темы.
2. Отметить на координатной плоскости множество точек, удовлетворяющих системе неравенств
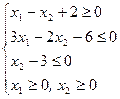
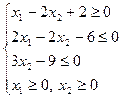
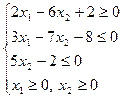
Сформулировать выводы относительно характера решений
*Примечание: занятие проводится в форме исследования с образованием несколько подгрупп для решения задач по тематике занятия; коллективный обмен результатами и анализ выявленных типичных ошибок.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 11 (тема 5)
В указанной ниже задаче требуется
1) Сформулировать задачу как задачу линейного программирования.
2) Найти решение задачи графическим методом.
Автотранспортное предприятие проводит закупку автобусов двух типов А и Б в количестве не более M машин, которые должны обеспечить одновременную перевозку не менее N пассажиров. Стоимость автобуса типа А - 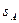 тыс. рублей, стоимость автобуса типа Б -
тыс. рублей, стоимость автобуса типа Б - 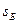 тыс. рублей. Количество пассажиров, которое может разместиться в одном автобусе типов А и Б, равно
тыс. рублей. Количество пассажиров, которое может разместиться в одном автобусе типов А и Б, равно 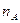 и
и 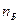 , соответственно. Сколько надо закупить автобусов каждого типа, чтобы минимизировать расходы?
, соответственно. Сколько надо закупить автобусов каждого типа, чтобы минимизировать расходы?
M=20; N = 1500; 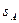 =800;
=800; 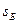 =300;
=300; 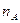 = 100;
= 100; 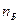 =60.
=60.
*Примечание: занятие проводится в форме исследования с образованием несколько подгрупп для решения задач по тематике занятия; коллективный обмен результатами и анализ выявленных типичных ошибок.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 12 (тема 5)
В указанной ниже задаче требуется
1) Сформулировать задачу как задачу линейного программирования.
2) Найти решение задачи графическим методом.
В ходе выборов кандидата для достижения успеха необходимо охватить теле- и радиорекламой не менее N тысяч человек (с повтором). Известно, что одна 30- секундная телереклама будет просмотрена n тысячами избирателей, одна 30- секундная радиореклама будет услышана m тысячами избирателей. Стоимость трансляции одного телефрагмента составляет 500$, а одного радиофрагмента - 100$. Всего планируется занять не менее t минут эфирного времени. Сколько теле- и радиофрагментов следует транслировать, чтобы минимизировать расходы.
N=720, n=24, m=4, t=40.
*Примечание: занятие проводится в форме исследования с образованием несколько подгрупп для решения задач по тематике занятия; коллективный обмен результатами и анализ выявленных типичных ошибок.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 13 (тема 6)
1. Повторение материала темы.
2. Определить области существования и области значений следующих функций:
а) 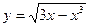 ; б)
; б) 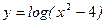 ; в)
; в) 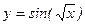 ; г)
; г) 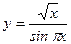 ;
;
д); 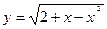 е)
е) 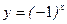 ; ж)
; ж) 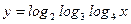 .
.
3. На какое множество 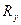 отображает множество
отображает множество 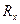 функция
функция 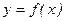
а) 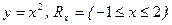 ; б)
; б) 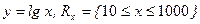
в) 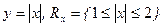 ; г)
; г) 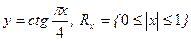 .
.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 14 (тема 7)
1. Повторение материала темы.
2. Вычислить пределы
а) 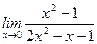 ; б)
; б) 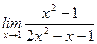 ; в)
; в) 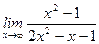 ; г)
; г) 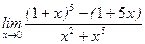 ;
;
д) 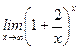 ; е)
; е) 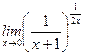 ; ж)
; ж) 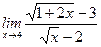 ; з)
; з) 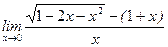 ;
;
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 15 (тема 8)
1. Повторение материала темы.
2. Найти первую и вторую производные функций:
а) 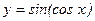 ; б)
; б) 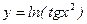 ; в)
; в) 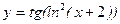 ; г)
; г) 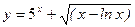 ;
;
д) 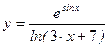 ; е)
; е) 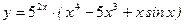 ; ж)
; ж) 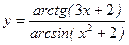 .
.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 16 (тема 8)
Найти первую и вторую производные функций:
а) 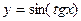 ; б)
; б) 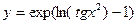 ; в)
; в) 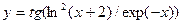 ; г)
; г) 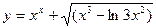 .
.
*Примечание: занятие проводится в форме организационно-деятельностной игры с разбиением группы на подгруппы и постановкой для 2-3-х подгрупп одинаковой задачи с последующим выбором в ходе коллективного обсуждения оптимального способа решения
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 17 (тема 8)
Написать уравнение касательной и нормали к графику функции 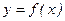 в заданной точке
в заданной точке 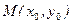
а) 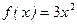 ,
, 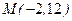 ; б)
; б) 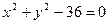 ,
, 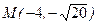 .
.
*Примечание: занятие проводится в форме организационно-деятельностной игры с разбиением группы на подгруппы и постановкой для 2-3-х подгрупп оди-наковой задачи с последующим выбором в ходе коллективного обсуждения оп-тимального способа решения
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 18 (тема 9)
1. Повторение материала темы.
2. Найти неопределенные интегралы методом непосредственного интегрирования
а) 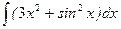 ; б)
; б) 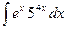 ; в)
; в) 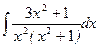 ; г)
; г) 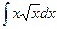 ; д)
; д) 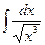 ;
;
е) 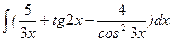 ; ж)
; ж) 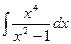 .
.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 19 (тема 9)
Найти неопределенные интегралы методом замены переменной
а) 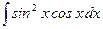 ; б)
; б) 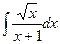 ; в)
; в) 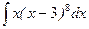 ; г)
; г) 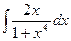 ;
;
д) 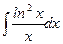 ; е)
; е) 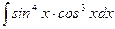 ; ж)
; ж) 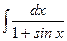 .
.
*Примечание: занятие проводится в форме организационно-деятельностной игры с разбиением группы на подгруппы и постановкой для 2-3-х подгрупп одинаковой задачи с последующим выбором в ходе коллективного обсуждения оптимального способа решения.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 20 (тема 9)
Найти неопределенные интегралы методом интегрирования по частям
а) 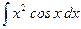 ; б)
; б) 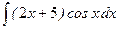 ; в)
; в) 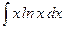 ; г)
; г) 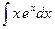 ; д)
; д) 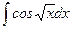
*Примечание: занятие проводится в форме организационно-деятельностной игры с разбиением группы на подгруппы и постановкой для 2-3-х подгрупп одинаковой задачи с последующим выбором в ходе коллективного обсуждения оптимального способа решения.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 21 (тема 10)
1. Повторение материала темы.
2. Доказать непосредственно сходимость рядов и найти их суммы
а) 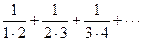 б)
б) 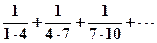
3. Исследовать сходимость знакопостоянного числового ряда
а) 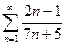 ; б)
; б) 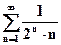 ; в)
; в) 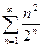 ;
;
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 22 (тема 11)
1. Полагая, что произвольная функция 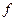 дифференцируема, проверить следующие равенства:
дифференцируема, проверить следующие равенства:
а) 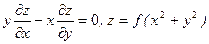 ; б)
; б) 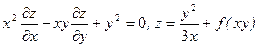 .
.
4. Найти величину и направление градиента функции в точке 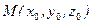
а) 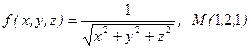 ; б)
; б) 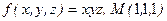 .
.
2. Найти точки локального экстремума функций и проверить в них выполнение достаточного условия экстремума
а)  ; б)
; б)  .
.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 23 (тема 11)
1. Используя метод множителей Лагранжа найти условный экстремум функции при заданных дополнительных условиях
а)  при условии
при условии  ;
;
б)  при условии
при условии  .
.
2. Вычислить двойные интегралы  по заданной области
по заданной области 
а) 
б)  ;
;
в)  ;
;
г)  ;
;
д)  ,
,  -треугольник с вершинами (1,1), (4,1), (4,4).
-треугольник с вершинами (1,1), (4,1), (4,4).
3. С помощью двойного интеграла найти площадь, ограниченную следующими кривыми:
а)  ;
;
б)  .
.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
Семинар 24 (тема 12)
Найти общее решение дифференциальных уравнений второго порядка
а)  ; б)
; б)  ;
;
в) 
*Примечание: занятие проводится в форме исследования с образованием несколько подгрупп для решения задач по заданной тематике; коллективное обсуждение результатов с анализом выявленных типичных ошибок.
Формируемые компетенции: ОК- 15, ОК-17, ПК-31, ПК-32, ПК-33.
