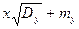Конгруэнтные процедуры

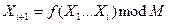
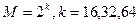
Мультипликативная

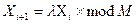
Условия:

X 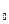-нечетное >0

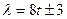
t-нечетное целое >0

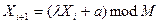
a-нечетное целое положительное число.

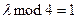
Сопоставление:

Критерий	аппар.метод	прогр.метод
1	2	3
1.формир. СЧ	+	-
2.формир. ПСЧ	+	+
3.надежность	-	+
4.быстродействие	+	-
5.простота реализац.	-	+
6.простота обслужив.	-	+
7.возможн. тиражиров.	-	+

Использование последовательностей равномерно распределенных случайных (псевдослучайных) чисел в задачах статистического моделирования.

1.Формирование случайных воздействий и внутренних характеристик систем, имеющих равномерное распределение.

2.Формирование случайного события или группы несовместных случайных событий.

3.Использование последовательностей в качестве базовых для формирования случайных чисел с заданным законом распределения.

Пусть A- случайное событие.

P(A)=P

P(ùA)=1-p

- +

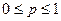
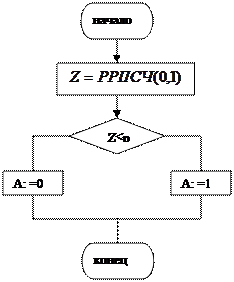Условия:

&

+ -

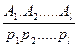
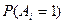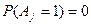
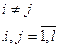
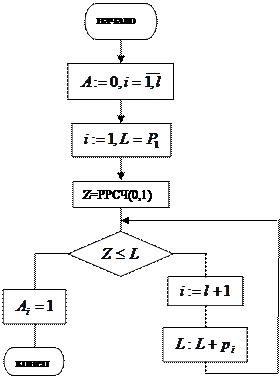
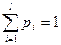
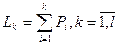
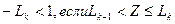
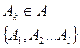
Формирование последовательности случайных чисел имеющих неравномерный закон распределения.

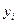-РРСЧ(0,1)

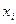-СЧ

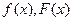
Методы:

а) метод обратной функции

б) метод Неймана

в) метод ступенчатой аппроксимации

Теорема:

а)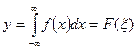

y- равномерно распределенная случайная величина (0,1)

Тогда 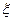имеет распределение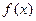

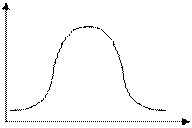б) f(x)

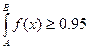
A B

Геометрическая интерпретация метода обратной функции

F(x)

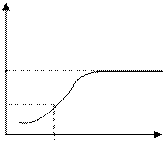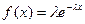
y_i

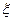
Метод обратной функции

Теорема: y-равномерно распределенная случайная величина (0,1)

Тогда 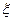распределена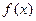

F(x) F^-1(x)

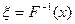
Алгоритм:

0 шаг- поиск обратной функции.

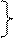1 шаг- формирование y-РРСЧ(0,1)

2 шаг- 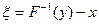{X_i}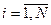

Метод обратной функции для экспоненциального закона.

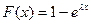
F(x)

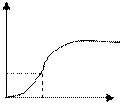
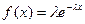
1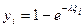

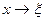
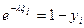
y_{i 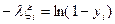,}тогда (1-y_i) тоже (0,1)

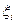x

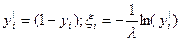
x1	x2	…	xl
F(x1)	F(x2)	…	F(xl)

F(x)-непрерывна, в данном случае дискретна.

Алгоритм:

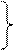1 шаг-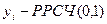

2 шаг- 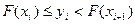N раз,N-длина последовательности.

3-шаг-реализация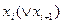

Метод Неймана

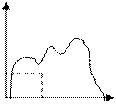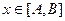=M

x₂

A x₁ B

1)

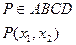
2)

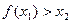
x₁-реализация

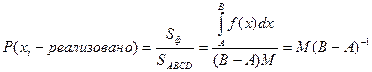
Метод ступенчатой аппроксимации

Геометрическая интерпретация:

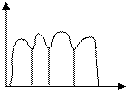
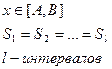
Задача: определить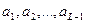

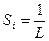
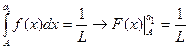
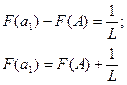
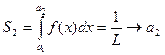
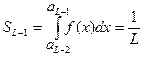
Алгоритм:

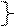1)Z₁-выбираем интервал

2)Z₂-РРСЧ(a_k,a_k+1) (реализация) N раз

Критерии сравнения 3-х методов:

1)простота (подготовки реализации)

2)точность

3)быстродействие

4)синхронность метода (если каждое обращение к процедуре результативно)

1. Метод обратной функции

· синхронный

· реализуется просто, если удается найти обратную функцию.

· метод точный, если удается точно определить обратную функцию F^-1(x)

· быстродействие

2. Метод Неймана

· асинхронный

· прост в реализации

· метод точный, если определена область определения функции

· быстродействие определяется вероятностью результативных обращений к процедуре

3. Метод ступенчатой аппроксимации

· синхронный

· сложный на этапе начальной подготовки, но прост при реализации.

· погрешность есть всегда, так как функция плотности распределения заменяется кусоной функцией.

· быстродействие зависит от количества интервалов.

Специализированный метод для реализации последовательности ПСЧ по нормальному закону распределения.

Теорема: Сумма РРСЧ есть СВ., распределенная по нормальному закону.

Дано:N-(кол-во чисел) РРСЧ (0,1)

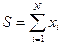
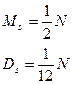
Сформировать СВ. по нормальному закону m=0,D=1

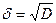
y - по нормальному закону распределения

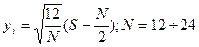,при N<12 характеристики неточные, при N>24 сложность

2)

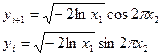
x₁,x₂-равномерно распределенная случайная величина (0,1)

y=