Тема 4. Дифференциальное исчисление функций многих переменных
Точечные множества в n-мерном пространстве. Понятие функции многих переменных. Примеры таких функций (линейная, квадратичная; в экономике – функция полезности, производственная функция). Область определения, линии уровня функций многих переменных. Функции полезности и кривые безразличия. Производственная функция. Предел и непрерывность функций многих переменных. Частные производные. Дифференциалы функций многих переменных. Производная по направлению, градиент. Экстремум, наибольшее и наименьшее значения функций многих переменных. Условный экстремум: метод подстановки и метод множителей Лагранжа. Метод наименьших квадратов.
Основные термины: линии уровня, частные производные, производная по направлению, локальный экстремум, условный экстремум.
Контрольные вопросы по теме 4:
1. Определить области существования функций:
а) 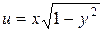 ; б)
; б) 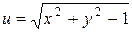 ; в)
; в) 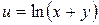 .
.
2. Построить линии уровня следующих функций:
а) 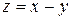 ; б)
; б) 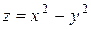 ; в)
; в) 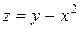 ; г)
; г) 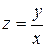 .
.
3. Найти частные производные первого порядка и дифференциал от следующих функций: а) 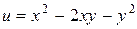 ; б)
; б) 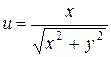 ; в)
; в) 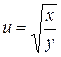 .
.
4. Найти производную по направлению 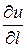 функции
функции 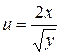 в точке
в точке 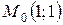 в направлении
в направлении 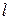 , образующим угол
, образующим угол 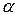 с осью абсцисс, если
с осью абсцисс, если 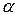 равен
равен 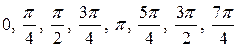 .
.
5. Найти критические точки функций и проверить в них выполнение достаточного условия экстремума:
а) 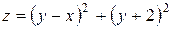 ; б)
; б) 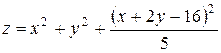 ;
;
в) 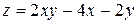 ; г)
; г) 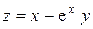 .
.
6. Найти наибольшее и наименьшее значения функции 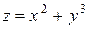 на полукруге единичного радиуса с центром в начале координат и расположенном в правой полуплоскости.
на полукруге единичного радиуса с центром в начале координат и расположенном в правой полуплоскости.
7. Найти наибольшее и наименьшее значения функции 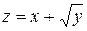 на треугольнике с вершинами в точках
на треугольнике с вершинами в точках 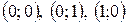 .
.
8. Методом наименьших квадратов найти эмпирическую формулу 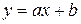 для функции, заданной следующей таблицей:
для функции, заданной следующей таблицей:
| x | –0,2 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |
| y | 3,2 | 2,9 | 1,8 | 1,6 | 1,2 | 0,7 |
Изобразить графически таблично заданную и соответствующую линейную функции. По формуле 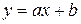 вычислить значение переменной y при
вычислить значение переменной y при 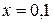 .
.
9. Определить оптимальное распределение ресурсов для функции выпуска 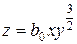 , если затраты на факторы x и y линейны и задаются ценами
, если затраты на факторы x и y линейны и задаются ценами 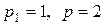 .
.
Тема 5. Интегральное исчисление
Первообразная функция и неопределенный интеграл. Свойства неопределённого интеграла. Неопределённый интеграл от основных элементарных функций. Интегрирование заменой переменного и по частям. Интегрирование рациональных, некоторых иррациональных функций и тригонометрических выражений. Понятие определённого интеграла, его геометрический и экономический смысл. Свойства определённого интеграла. Формула Ньютона-Лейбница. Замена переменного и формула интегрирования по частям в определённом интеграле. Геометрические приложения определённого интеграла. Несобственные интегралы.
