Функции одной переменной
Т.Э.Захарова
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Учебное пособие
(специальность «Информационная безопасность телекоммуникационных систем», факультет АЭС)
Новосибирск
УДК 517 (075.8)
Т.Э.Захарова. Математический анализ: Учебное пособие (специальность «Информационная безопасность телекоммуникационных систем», факультет АЭС)/ СибГУТИ.– Новосибирск, 2013г. - 51 стр.
Учебное пособие содержит материал для подготовки и проведения практических занятий по математическому анализу со студентами 1 курса, а также задачи для домашних работ в объеме, требуемом государственным образовательным стандартом для подготовки дипломированных специалистов в соответствии с разработанными рабочими и учебными программами. В пособие включены типовые задачи, а также справочный теоретический материал.
Для направления 090302 «Информационная безопасность».
Кафедра высшей математики СибГУТИ
Ил. 2, список лит.- 4 наименования
Рецензенты: гл. науч.сотр. Института ВТ СО РАН,
профессор кафедры математического моделирования ММФ НГУ, д. ф.-м. н. Черных Г.Г.;
доцент кафедры инженерной математики факультета ФПМИ НГТУ,
к.т.н. Шеремет О.В.;
доцент кафедры высшей математики СибГУТИ Храмова Т.В.
Утверждено редакционно-издательским советом СибГУТИ в качестве учебного пособия.
© Сибирский государственный университет
телекоммуникаций и информатики, 2013
ОГЛАВЛЕНИЕ
| Комплексные числа………………………………………………………………….. | |
| Функции одной переменной……………………………………………………….... | |
| Предел функции. Раскрытие неопределенностей. Замечательные пределы…….. | |
| Сравнение бесконечно малых и бесконечно больших величин………………….. | |
| Непрерывные функции. Точки разрыва……………………………………………. | |
| Дифференцирование функций……………………………….................................... | |
| Правило Лопиталя…………………………………………………………………… | |
| Исследование функций и построение их графиков……………………………….. | |
| Функции двух переменных…………………………………………………………. | |
| Неопределенный интеграл. Простейшие методы интегрирования..……..……… | |
| Неопределенный интеграл. Интегрирование по частям ………………………… | |
| Неопределенный интеграл. Интегрирование дробно-рациональных функций……………………………………………………………………………… | |
| Неопределенный интеграл. Интегрирование тригонометрических функций… | |
| Неопределенный интеграл. Интегрирование иррациональных функций……… | |
| Определенный интеграл…………………………………………………………….. | |
| Приложения определенного интеграла…………………………………………….. | |
| Несобственные интегралы………………………………………………………….. | |
| Двойной интеграл…………………………………………………………………… | |
| Тройной интеграл…………………………………………………………………… | |
| Дифференциальные уравнения первого порядка………………………………….. | |
| Дифференциальные уравнения второго порядка………………………………….. | |
| Операционное исчисление…………………………………………………………... | |
| Справочный материал…………………………………………………………......... | |
| Приложения…………………………………………………………………………... | |
| Литература…………………………………………………………………………… |
Комплексные числа
Вычислить:
1. 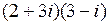 | 2. 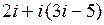 | 3. 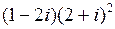 | 4. 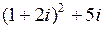 |
5. 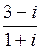 | 6. 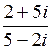 | 7. 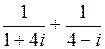 | 8. 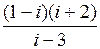 |
Изобразить комплексное число точкой на плоскости, найти модуль и аргумент, записать число в тригонометрической и показательной формах:
9. 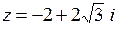 | 10. 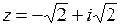 | 11. 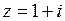 | 12. 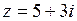 |
13. 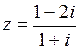 | 14. 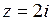 | 15. 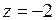 |
Вычислить:
16. 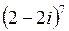 | 17. 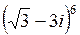 | 18. 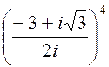 | 19. 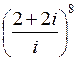 |
Вычислить корни из комплексного числа:
20. 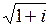 | 21. 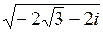 | 22. 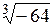 | 23. 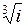 |
Решить уравнения:
24. 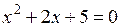 | 25. 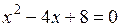 | 26. 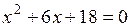 |
27. 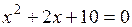 | 28. 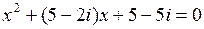 | 29. 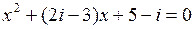 |
Ответы.1. 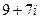 . 2.
. 2. 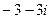 . 3.
. 3.  . 4.
. 4. 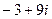 . 5.
. 5. 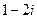 . 6.
. 6. 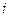 . 7.
. 7. 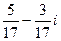 . 8.
. 8. 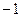 .
.
9. 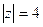 ,
, 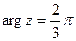 . 10.
. 10. 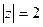 ,
, 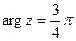 . 11.
. 11. 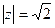 ,
, 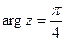 . 12.
. 12. 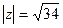 ,
,
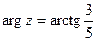 . 13.
. 13. 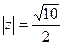 ,
, 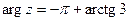 . 14.
. 14. 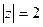 ,
, 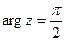 . 15.
. 15. 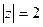 ,
, 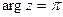 .
.
16. 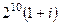 . 17.
. 17. 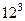 . 18.
. 18. 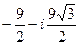 . 19.
. 19. 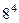 . 20.
. 20. 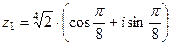 ,
,
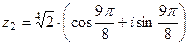 . 21.
. 21. 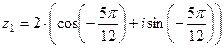 ,
, 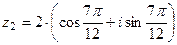 .
.
22. 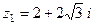 ,
, 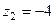 ,
, 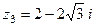 . 23.
. 23. 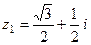 ,
, 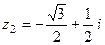 ,
, 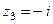 .
.
24. 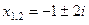 . 25.
. 25. 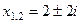 . 26.
. 26. 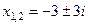 . 27.
. 27. 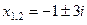 . 28.
. 28. 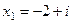 ,
,
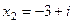 . 29.
. 29. 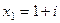 ,
, 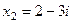 .
.
Функции одной переменной
30. Для заданной функции найти 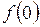 ,
, 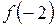 ,
, 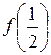 ,
, 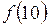 :
:
а) 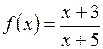 ; б)
; б) 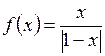 .
.
31. Дана функция 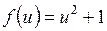 . Найти
. Найти 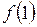 ,
, 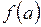 ,
, 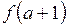 ,
, 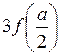 .
.
32. Дана функция 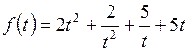 . Найти
. Найти 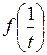 .
.
33. Дана функция 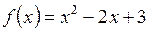 . Найти корни уравнения:
. Найти корни уравнения:
а) 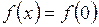 ; б)
; б) 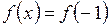 .
.
34. Дана функция 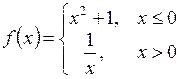 . Найти
. Найти 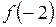 ,
, 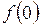 ,
, 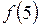 .
.
35. Дана функция 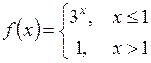 . Найти
. Найти 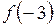 ,
, 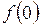 ,
, 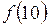 .
.
Найти область определения следующих функций:
36. 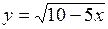 . 37.
. 37. 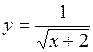 . 38.
. 38. 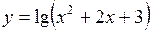 .
.
39. 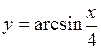 . 40.
. 40. 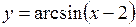 . 41.
. 41. 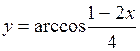 .
.
42. 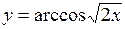 . 43.
. 43. 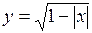 . 44.
. 44. 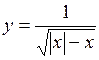 .
.
45. 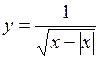 . 46.
. 46. 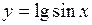 .
.
47. 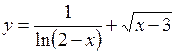 . 48.
. 48. 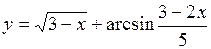 .
.
49. 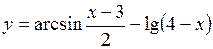 . 50.
. 50. 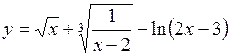 .
.
51. 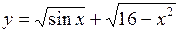 . 52.
. 52. 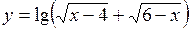 .
.
Представить в виде цепочки основных элементарных функций:
53. 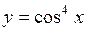 . 54.
. 54. 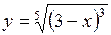 . 55.
. 55. 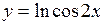 .
.
56. 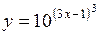 . 57.
. 57. 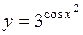 . 58.
. 58. 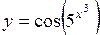 .
.
Выяснить, какие из функций являются четными, какие нечетными и какие общего вида:
59. 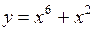 . 60.
. 60. 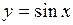 . 61.
. 61. 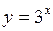 .
.
62. 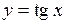 . 63.
. 63. 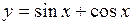 . 64.
. 64. 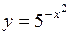 .
.
65. 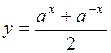 . 66.
. 66. 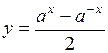 . 67.
. 67. 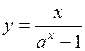 .
.
68. 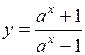 . 69.
. 69. 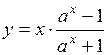 . 70.
. 70. 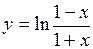 .
.
Найти нули и интервалы знакопостоянства функции:
71. 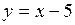 . 72.
. 72. 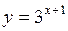 . 73.
. 73. 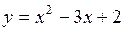 . 74.
. 74. 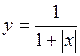 .
.
Используя графики основных элементарных функций, построить графики следующих функций:
75. 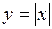 . 76.
. 76. 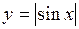 . 77.
. 77. 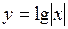 . 78.
. 78. 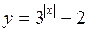 .
.
79. 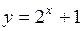 . 80.
. 80. 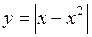 . 81.
. 81. 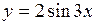 . 82.
. 82. 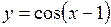 .
.
83. 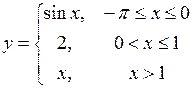 . 84.
. 84. 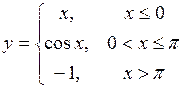 .
.
Ответы.30. а)  ,
, 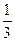 ,
, 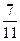 ,
, 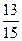 ; б) 0,
; б) 0, 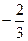 , 1,
, 1, 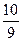 . 31. 2,
. 31. 2, 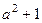 ,
, 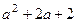 ,
, 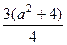 .
.
32. 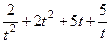 . 33. а)
. 33. а) 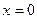 ,
, 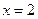 ; б)
; б) 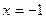 ,
, 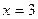 . 34. 5, 1,
. 34. 5, 1, 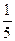 . 35.
. 35. 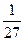 , 1, 1.
, 1, 1.
36. 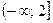 . 37.
. 37. 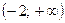 . 38.
. 38. 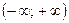 . 39.
. 39. 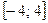 . 40.
. 40. 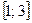 . 41.
. 41. 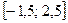 .
.
42. 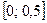 . 43.
. 43. 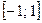 . 44.
. 44. 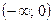 . 45.
. 45.  . 46.
. 46. 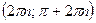 ,
, 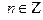 . 47.
. 47. 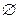 .
.
48. 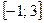 . 49.
. 49. 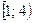 . 50.
. 50. 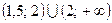 . 51.
. 51. 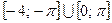 . 52.
. 52. 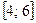 . 53.
. 53. 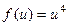 ,
,
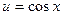 . 54.
. 54. 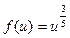 ,
, 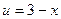 . 55.
. 55. 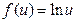 ,
, 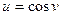 ,
, 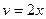 . 56.
. 56. 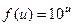 ,
,
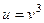 ,
, 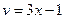 . 57.
. 57. 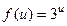 ,
, 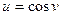 ,
, 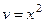 . 58.
. 58. 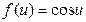 ,
, 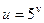 ,
, 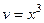 .
.
59. Четная. 60. Нечетная. 61. Общего вида. 62. Нечетная. 63. Общего вида.
64. Четная. 65. Четная. 66. Нечетная. 67. Общего вида. 68. Нечетная. 69. Четная.
70. Нечетная. 71. 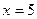 ,
, 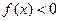
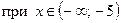 ,
, 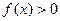 при
при 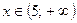 . 72. Нулей
. 72. Нулей
функции нет, 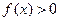
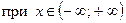 . 73.
. 73. 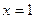 ,
, 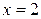 ,
, 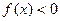
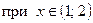 ,
,
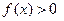
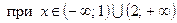 . 74. Нулей функции нет,
. 74. Нулей функции нет, 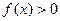 при
при 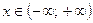 .
.
