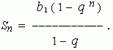Дифференциальные уравнений, допускающих понижение порядка

I. Уравнение вида 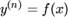. После n-кратного интегрирования получается общее решение

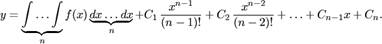
II. Уравнение не содержит искомой функции и её производных до порядка 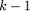включительно:

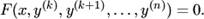
Порядок такого уравнения можно понизить на 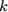единиц заменой 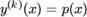. Тогда уравнение примет вид

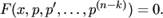
Дифференциального уравнения второго порядка с постоянными коэффициентами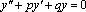

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид 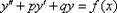, где p и q – произвольные действительные числа, а функция f(x) – непрерывна на интервале интегрирования X.

__

Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).

Числовым рядом называется выражение вида 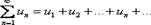где – действительные или комплексные числа, называемые членами ряда, 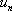- общим членом ряда.

Гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда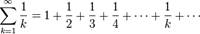

Частичная сумма числового ряда – это сумма вида 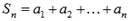, где n – некоторое натуральное число.

Суммой числового ряда это предел частичных сумм Sn, если он существует и конечен

Сходящимся называется числовой ряд 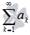если существует конечный предел последовательности частичных сумм 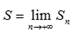. Это значит, что бесконечная сумма равна некоторому конечному числу S

Расходящимся называется если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд

Суммой сходящегося числового ряда называется предел последовательности его частичных сумм, то есть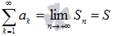

Знакоположительным числовой ряд 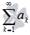если все его члены положительны, то есть, .

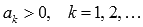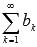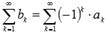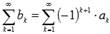Знакочередующимся числовой ряд если знаки его соседних членов различны. Знакочередующийся числовой ряд можно записать в виде или , где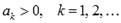

Знакопеременным числовой ряд 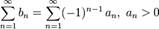если он содержит бесконечное множество как положительных, так и отрицательных членов.

Признак Лейбница:

1. 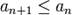(монотонное невозрастание {an} по абсолютной величине)

2. 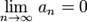Тогда этот ряд сходится.

Абсолютно сходящимся знакопеременный ряд 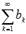, если сходится ряд из абсолютных величин его членов, то есть, сходится знакоположительный числовой ряд .

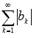Условно сходящимся знакопеременный ряд , если ряд 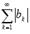расходится, а ряд 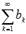сходится

Арифметическая прогрессия. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом d

Число d называется разностью прогрессии.

Член арифметической прогрессии вычисляется по формуле: an = a1 + d ( n – 1 )

Геометрическая прогрессия. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число q

Число q называется знаменателем прогрессии.

Член геометрической прогрессии вычисляется по формуле: bn = b1 q n - 1 .

Сумма n первых членов геометрической прогрессии вычисляется как: