Теорема умножения вероятностей
Вероятность произведения событий А и В (или вероятность их совместного наступления) равна произведению вероятности наступления первого события на условную вероятность наступления второго, вычисленную в предположении, чтопервое событие имело место.
Символически:Р(А´В)=Р(А)´ 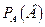
Следствие 1. В силу симметрии, т.к. А´В=В´А, то
Р(А´В)=Р(В´А)=Р(В)´ 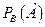
Следствие 2. Для независимых событий:
Р(А´В)=Р(А)´Р(В)
· У мышей черная окраска шерсти – доминантный признак, коричневый окрас – рецессивный. Предположим, что скрещиваются две гетерозиготные мыши, причем при каждом скрещивании в помете – четыре потомка. Оценим вероятности всех возможных вариантов окраса шерсти потомков.
1) Обозначим события: E1= {все четыре мышонка – коричневого окраса},
А={первый мышонок - коричневый},
В={второй мышонок - коричневый},
С={третий мышонок - коричневый},
D={четвертый мышонок - коричневый}.
Тогда E1=А´В´С´D. По теореме умножения вероятностей для независимых событий
Р(E1)=Р(А)´Р(В)´Р(С)´Р(D). В соответствии с первым законом Менделя:
Р(E1)= 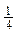 ´
´ 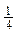 ´
´ 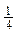 ´
´ 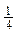 =
= 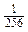
2) E2={в помете три коричневых и один черный мышонок}.
При этом черный может быть первым (A1), вторым (A2), третьим (A3) или четвертым (A4).
Графически: Так как E2 =A1+A2+ A3+ A4.
Þ Р( 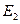 )=Р(
)=Р( 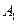 )+Р(
)+Р( 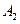 )+Р(
)+Р( 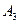 )+Р(
)+Р( 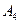 )
)
● ○ ○ ○ (в силу несовместимости событий 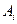 ).
).
○ ● ○ ○
○ ○ ● ○ По теореме умножения вероятностей:
○ ○ ○ ●
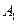
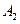
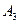
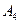 Р(
Р( 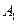 ) = Р(
) = Р( 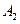 ) = Р(
) = Р( 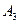 ) = Р(
) = Р( 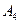 ) =
) = 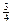 ´
´ 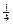 ´
´ 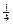 ´
´ 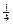
Откуда Р( 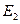 ) = 4´
) = 4´ 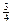 ´
´ 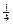 ´
´ 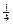 ´
´ 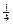 =
= 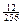
3) E3= {в помете 2 коричневых и 2 черных мышонка}.
Черные могут быть: «Первый и второй» ( 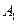 ), «Первый и третий» (
), «Первый и третий» ( 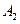 ), «Первый и четвертый» (
), «Первый и четвертый» ( 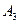 ), «Второй и третий» (
), «Второй и третий» ( 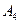 ), «Второй и четвертый» (
), «Второй и четвертый» ( 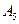 ), «Третий и четвертый» (
), «Третий и четвертый» ( 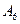 ).
).
Графически: Так как 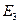 =
= 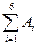 Þ
Þ
● ● ● ○ ○ ○
● ○ ○ ● ● ○ Р( 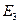 ) =
) = 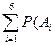 ) = 6´
) = 6´ 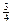 ´
´ 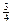 ´
´ 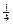 ´
´ 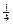 =
= 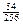
○ ● ○ ● ○ ● (в силу несовместимости событий 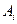 ).
).
○ ○ ● ○ ● ●

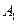
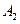
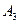
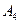
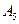
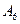
4) E4= {в помете 1 коричневый и 3 черных мышонка}.
Коричневый может быть: «первым» ( 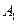 ), «вторым» (
), «вторым» ( 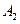 ), «третьим» (
), «третьим» ( 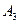 ) или «четвертым» (
) или «четвертым» ( 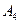 ).
).
Графически: 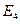 =
= 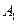 +
+ 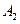 +
+ 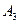 +
+ 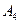 Þ
Þ
○ ● ● ● Р( 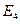 )=
)= 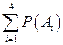 =4´
=4´ 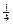 ´
´ 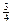 ´
´ 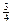 ´
´ 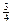 =
= 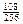 .
.
● ○ ● ● (в силу несовместимости 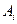 )
)
● ● ○ ●
● ● ● ○
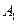
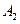
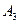
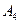
5) E5= {все четыре мышонка – черного (доминантного) окраса}.
Обозначим события:
А={первый мышонок - черный},
В={второй мышонок - черный},
С={третий мышонок - черный},
D={четвертый мышонок - черный}.
Тогда: E5=А´В´С´D Þ Р( 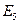 )=Р(А)´Р(В)´Р(С)´Р(D)=
)=Р(А)´Р(В)´Р(С)´Р(D)= 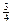 ´
´ 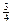 ´
´ 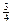 ´
´ 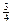 =
= 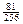
Замечание: События 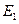 ,
, 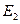 ,
, 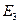 ,
, 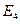 ,
, 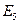 образуют полную группу и
образуют полную группу и 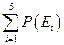 =
= 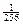 +
+ 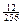 +
+ 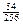 +
+ 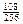 +
+ 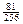 = 1.
= 1.
Теорема сложения вероятностей(для случая совместных событий)
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления.
Р(А+В) = Р(А) + Р(В) – Р(А´В)
· Известно, что в посевах пшеницы (на делянке) 95% здоровых растений. Выбирают два растения. Какова вероятность, что среди них хотя бы одно окажется здоровым?
- Обозначим: А={первое растение - здоровое},
В = {второе растение - здоровое},
С = {хотя бы одно растение - здоровое}.
Очевидно, С=А+В Þ Р(С)=Р(А+В)=Р(А)+Р(В)-Р(А´В)=0,95+0,95-0,95´0,95=0,9975
