Остаточное время жизни
Страховая компания имеет дело с конкретными людьми, дожившими до определенного возраста. Статистические свойства времени жизни таких людей существенно отличаются от свойств времени жизни новорожденных. Если человек в возрасте  лет обратился в страховую компанию (в актуарной математике такого человека обозначают
лет обратился в страховую компанию (в актуарной математике такого человека обозначают 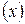 ), то заведомо известно, что он дожил до
), то заведомо известно, что он дожил до  лет, и поэтому все случайные события, связанные с этим человеком, должны рассматриваться при условии, что
лет, и поэтому все случайные события, связанные с этим человеком, должны рассматриваться при условии, что 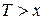 .
.
Для человека в возрасте  лет обычно рассматривают не продолжительность жизни
лет обычно рассматривают не продолжительность жизни 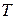 , а остаточное время жизни
, а остаточное время жизни 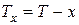 . Распределение случайной величины
. Распределение случайной величины 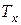 – это условное распределение величины
– это условное распределение величины 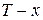 при условии, что
при условии, что 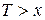 :
:
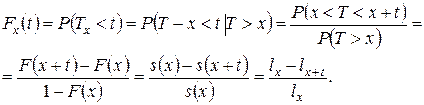
Соответствующая функция выживания 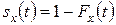 определяется формулой
определяется формулой
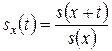 ,
,
так что плотность случайной величины 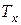 может быть найдена по формуле:
может быть найдена по формуле:
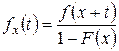 ,
, 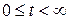 .
.
Интенсивность смертности, связанная с величиной 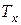 , есть
, есть
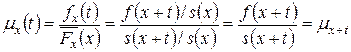 .
.
Это соотношение означает, что интенсивность смертности спустя время  для человека, которому сейчас
для человека, которому сейчас  лет, равна интенсивности смертности в возрасте
лет, равна интенсивности смертности в возрасте 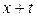 для новорожденного. Другими словами, интенсивность смертности в данном возрасте
для новорожденного. Другими словами, интенсивность смертности в данном возрасте 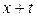 не зависит от уже прожитых лет.
не зависит от уже прожитых лет.
Основные величины, связанные с остаточным временем жизни
Вероятность 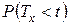 (т.е. вероятность смерти человека возраста
(т.е. вероятность смерти человека возраста  в течение ближайших
в течение ближайших  лет) в актуарной математике обозначается
лет) в актуарной математике обозначается 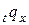 . Тогда
. Тогда
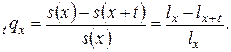
Дополнительная вероятность 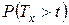 (т.е. вероятность того, что человек в возрасте
(т.е. вероятность того, что человек в возрасте  лет проживет еще по меньшей мере
лет проживет еще по меньшей мере  лет) в актуарной математике обозначается
лет) в актуарной математике обозначается 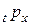 :
:
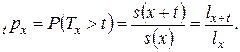
Случай 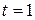 играет особую практическую роль и встречается наиболее часто. Для него принято опускать передний индекс у переменных
играет особую практическую роль и встречается наиболее часто. Для него принято опускать передний индекс у переменных 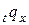 и
и 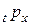 . Таким образом, символ
. Таким образом, символ 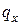 обозначает вероятность того, что человек в возрасте
обозначает вероятность того, что человек в возрасте  лет умрет в течение ближайшего года, а символ
лет умрет в течение ближайшего года, а символ 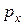 обозначает вероятность того, что человек в возрасте
обозначает вероятность того, что человек в возрасте  лет проживет еще по крайней мере один год. Тогда
лет проживет еще по крайней мере один год. Тогда
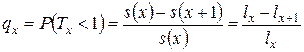 ,
, 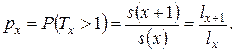
С помощью вероятностей 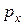 можно вычислить и более общие вероятности
можно вычислить и более общие вероятности 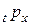 :
:
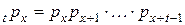 .
.
Рассмотрим теперь более общее событие, заключающееся в том, что человек возраста  проживет еще
проживет еще  лет, но умрет на протяжении последующих
лет, но умрет на протяжении последующих 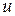 лет, т.е.
лет, т.е. 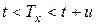 . Его вероятность обозначается
. Его вероятность обозначается 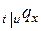 :
:
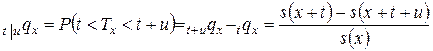 .
.
Случай 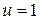 представляет особый интерес для приложений к страхованию жизни. Как обычно соответствующий индекс принято опускать. Таким образом,
представляет особый интерес для приложений к страхованию жизни. Как обычно соответствующий индекс принято опускать. Таким образом, 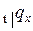 – это вероятность того, что человек в возрасте
– это вероятность того, что человек в возрасте  лет проживет еще
лет проживет еще 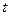 лет, но умрет на протяжении следующего года.
лет, но умрет на протяжении следующего года.
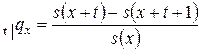 .
.
Макрохарактеристики остаточного времени жизни
Среднее значение остаточного времени жизни человека в возрасте  лет
лет 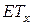 обозначается
обозначается 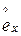 и называется полной ожидаемой продолжительностью жизни:
и называется полной ожидаемой продолжительностью жизни:
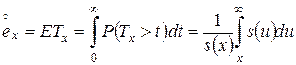 .
.
Второй момент можно найти по формуле:
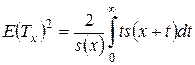 .
.
Среднее остаточное время жизни можно выразить и через другие характеристики времени жизни. Для этого рассмотрим группу из 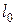 новорожденных и обозначим через
новорожденных и обозначим через 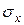 суммарное число лет, прожитых представителями этой группы в возрасте
суммарное число лет, прожитых представителями этой группы в возрасте  и более. Таким образом, если время жизни i-того представителя группы,
и более. Таким образом, если время жизни i-того представителя группы, 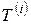 , меньше чем
, меньше чем  , его вклад в сумму
, его вклад в сумму 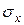 равен нулю. Если же
равен нулю. Если же 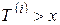 , то вклад в сумму равен
, то вклад в сумму равен 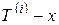 .
.
Тогда
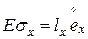 .
.
Среднее значение величины 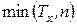 , где
, где  – некоторая положительная константа, называют частичной средней продолжительностью жизни и обозначают
– некоторая положительная константа, называют частичной средней продолжительностью жизни и обозначают 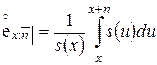 .
.
