Из полученного следует
Переходя к оригиналам, с учетом теоремы запаздывания, получим
(8.49)
Это и есть рекуррентная формула для вычисления дискретных значений выходной величины.
Очень часто дискретно – непрерывная система задана в виде структурной схемы и желательно получить разностные уравнения непрерывных динамических звеньев непосредственно по их передаточным функциям. Для этой цели распрстранение нашли методы подстановки, связанные с заменой s =f(z). При этом должны выполняться следующие требования:
1)если непрерывная передаточная функция W(s) соответствует устойчивой системе, то и полученная передаточная функция W(z) должна определять устойчивую систему;
2)способ должен допускать возможность раздельного применения к звеньям структурной схемы;
3) для постоянных сигналов коэффициент усиления дискретной цепи должен соответствовать тем же значениям коэффициента усиления непрерывной цепи.
Перечисленным требованиям наиболее полно удовлетворяет подстановка Тастина
(8.50)
Подстановка Тастина дает хорошие результаты при 
где 
основная постоянная времени непрерывной системы. В некоторых изданиях рекомендуют выбирать 
Этим требованиям не всегда удается удовлетворить и в таких случаях можно использовать модифицированную подстановку Тастина
(8.51)
При неизменном значении периода дискретизации удовлетворительное соответствие динамики непрерывной системы с ее дискретной моделью иногда можно получить подбором параметра Тастина w. Полученная подстановкой Z – передаточная функция описанным выше способом преобразуется в рекуррентную формулу.
Для получения дискретной модели непрерывной системы можно использовать метод подбора корня, который заключается в выполнении следующих операций:
1) определение нулей и полюсов передаточной функции непрерывной системы;
2) отображение нулей и полюсов s – плоскости в z – плоскости, исппользуя соотношения
1) образование полиномов Z – передаточной функции с полюсами и нулями, определенными в п.2;
2) определение конечного значения реакции непрерывной системы на единичное ступенчатое воздействие;
3) определение конечного значения реакции дискретной системы на единичное ступенчатое воздействие;
4) подбор конечного значения дискретной системы в соответствии с конечным значением непрерывной системы введением постоянной в передаточную функцию, образованную в п.3;
5) добавление нулей в передаточную функцию дискретной системы до получения m =n – 1.
6) Определение моделирующего разностного уравнения.
Для использования рассмотренного способа непрерывная система должна удовлетворять следующим требованиям:
1) быть асимптотически устойчивой и удовлетворять теореме о конечном значении;
2) конечное значение не должно равняться нулю.
Пример. Методом подбора корня получить разностное уравнение для моделирования на ЦВМ непрерывной системы, имеющей передаточную функцию
Параметры передаточной функции те же, что и в предыдущем примере.
Нулей передаточная функция не имеет, а полюсы комплексно сопряженные и равные a± jb, где a = -0.6, b = 1.908. Передаточную функцию моделирующей дискретной системы запишем в виде
После преобразований и умножения на пока неизвестный коэффициент k, получим
Конечное значении реакции непрерывной системы на единичное ступенчатое воздействие будет
Конечное значение реакции дискретной системы на то же воздействие определится как
Для того, чтобы конечные значения реакций непрерывной и дискретной систем были равны, коэффициент k должен быть равен
Подставив коэффициент усиления, а так же значения a и b и дополнив передаточную функцию дискретной системы одним нулем, получим
По этой передаточной функции можно получить моделирующее разностное уравнение и рекуррентную формулу, по которой и рассчитан переходный процесс, показанный на рис.8.14.
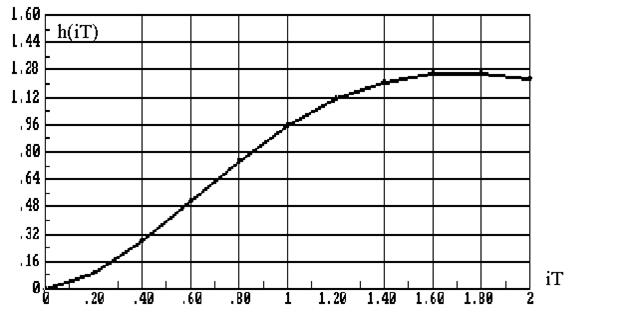
Рис.8.14. Переходный процесс, полученный при использовании
метода подбора корня
Полученная переходная функция с достаточно высокой точностью соответствует переходной функции исходной непрерывной системы.