Раздел IV Дифференциальные уравнения
Тема 5 Дифференциальные уравнения
Понятие о дифференциальных уравнениях. Общее и частное решения. Задача Коши. Задача о построении математической модели демографического процесса. Дифференциальные уравнения первого порядка (неполные, с разделяющимися переменными, однородные и линейные). (1, гл. 12, § 12.1, 12.4–12.7, с. 325–328; 334–340); (2, гл. 2).
Студентам необходимо усвоить определение дифференциального уравнения – как уравнения, которое связывает искомую функцию одной или нескольких переменных и производные различных порядков данной функции.
Дифференциальные уравнения от одной переменной называется обыкновенным дифференциальным уравнением, в дифференциальные уравнения от нескольких переменных – дифференциальные уравнения в частных производных.
Порядок дифференциального уравнения равен порядку старшей степени производной xy¢¢¢-xy¢+5=0 – уравнение третьего порядка.
Нужно помнить, что задача интегрирования дифференциального уравнения – это задача нахождения искомого решения, а график решения называется интегральной кривой.
Общее решение дифференциального уравнения – это решение, которое является функцией переменных х и n произвольных независимых постоянных С1, С2, С0…,Сn.
Частное решение дифференциального уравнения – это решение, полученное из общего при некоторых значениях постоянных.
Для ряда типов дифференциальных уравнений нужно знать студенту основные понятия, нужно уметь решать однородные дифференциальные уравнения, линейные дифференциальные уравнения, неполные дифференциальные уравнения и дифференциальные уравнения с разделяющимися переменными.
Разобрать задачи (1, 12.8–12.22, 12.31–12.32, 12.45–12.47, 12.65). Решить самостоятельно (2, 12.17–12.30, 12.48–12.57, 12.62–12.69, 12.78).
Таблица соотношения начальной буквы фамилии студента и варианта контрольных заданий
| Начальная буква фамилии | Вариант задания |
| А, Е, Л | Первый |
| Р, Х, Э | Второй |
| Б, Ж, М | Третий |
| С, Ц, Ю | Четвертый |
| В, З, Н | Пятый |
| Т, Ч | Шестой |
| Г, И, О | Седьмой |
| У, Ш | Восьмой |
| Д, К, П | Девятый |
| Ф, Щ, Я | Десятый |
ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ
ВАРИАНТ №1
Задание № 1. Исследовать несобственный интеграл на сходимость

Задание № 2. Вычислить сумму ряда 
Задание № 3. Исследовать ряды на сходимость
1.  2.
2. 
Задание № 4. Найти область сходимости степенного ряда: 
Задание № 5. Решить дифференциальное уравнение:
х2dу = у2dх, если при х = 1; у = 1.
Задание № 6. Найти общее решение дифференциального уравнения, удовлетворяющее начальным условиям, и частное решение
 .
.
Задание № 7. Разложить на отрезке 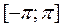 в ряд Фурье и построить график суммы ряда для функции:
в ряд Фурье и построить график суммы ряда для функции: 
ВАРИАНТ №2
