Лекция 15. ГЕНЕРАЛЬНАЯ СРЕДНЯЯ И ВЫБОРОЧНАЯ СРЕДНЯЯ

Пусть требуется изучить дискретную генеральную совокупность относительно количественного признака, генеральной средней.

Генеральная средняя ‒ среднее арифметическое значений признака генеральной совокупности:

1. Если значения признака различны, то

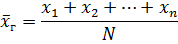
или

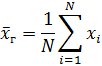
2. Если значения признака имеют частоты

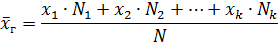
или

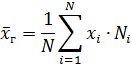
Выборочной средней называется среднее арифметическое значений признака выборочной совокупности.

1. Если значения признака различны, то

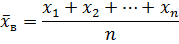
или

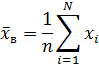
2. Если значения признака имеют частоты

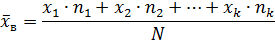
или

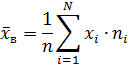
Если числовой признак X считать случайной величиной X, то генеральная средняя ‒ генеральное математическое ожидание, а выборочная средняя ‒ выборочное математическое ожидание: , .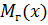

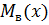Генеральная выборочная и исправленная дисперсия.

Генеральной дисперсией 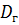называется среднее арифметическое квадратов отклонений значений признака 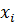отих генеральной средней:

1. Если значения признака различны, то

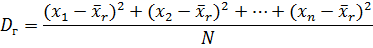
2. Если значения признака имеют частоты, то

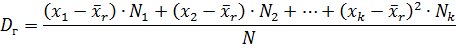
или

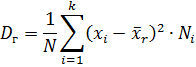
Выборочная дисперсия ‒ среднее арифметическое квадратов отклонений значений признака от их выборочной средней.

1. Если значения признака различны, то

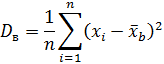
2. Если значения признака имеют частота, то

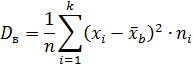
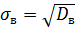
Пример.

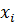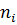Найти: .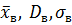

Решение:

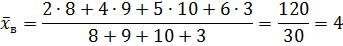
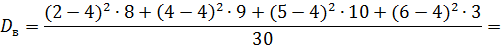
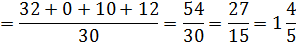
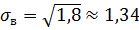
Для вычисления дисперсии используют еще одну формулу.

Дисперсия (любая) равна разности среднего арифметического квадратов значений признака и квадрата общей средней:

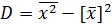
Пример.

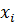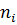Решение:

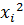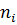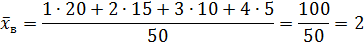
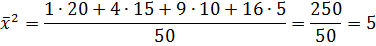
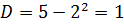
Выборочная дисперсия при выборках малого объема имеет систематическую ошибку, чтобы ее избежать, дисперсию умножают на число
.

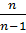Полученная дисперсия называется исправленной дисперсией и обозначается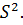

Итак,

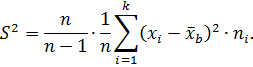
Следовательно,

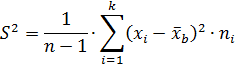
Тогда 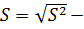исправленное среднее квадратическое отклонение.

При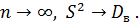

Лекция 16. ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ. ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ, ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ.

Точечной оценкой некоторого параметра называют оценку, определяемую одним числом.

При выборках малого объема точечная оценка может значительно отличаться от оцениваемого параметра.Поэтому при небольшом объеме выборки пользуются интервальными оценками.

Интервальной оценкой некоторого параметра 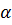называют числовой интервал 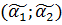, который с заданной вероятностью 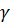покрывает значение параметра .

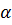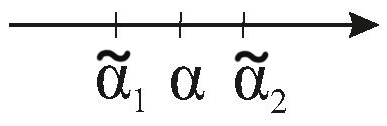
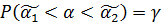
Где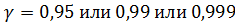

Интервал 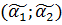называется доверительным интервалом, а вероятность 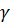называется доверительной вероятностью или надежностью оценки.