Поперечный изгиб прямого бруса. Вывод дифференциальных зависимостей между интенсивностью внешней поперечной нагрузки, внутренней поперечной силой и внутренним изгибающим моментом
Поперечный изгиб прямого бруса – см. в вопросе 20.
Интенсивность распределённой внешней нагрузки q(z) является первой производной внутренней поперечной силы Qy по продольной координате z балки:
 ,
,  ,
, 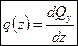 .
.
Внутренняя поперечная сила Qy – есть первая производная от внутреннего изгибающего момента Мх по продольной координате z балки:
 ,
,  ,
,  ,
,  - теорема Журавского Д.И.
- теорема Журавского Д.И.

Определение внутренних усилий, возникающих в поперечных сечениях стержневых элементов плоской статически определимой рамы, нагруженной системой внешних усилий, действующих в плоскости рамы. Правила знаков для внутренних усилий.
- Найти реакции связей, наложенных на раму.
- Методом сечений определить внутренние усилия.
Если сумма продольных сил, действующих на отсечённую часть рамы, положительная, то ордината силы Nz в сечении откладывается вверх. Если же сумма продольных сил, действующих на отсечённую часть рамы, отрицательная, то ордината силы Nz в сечении откладывается вниз.
Если сумма поперечных сил, действующих на отсечённую часть рамы, положительная, то ордината силы Qy в сечении откладывается вверх. Если же равнодействующая поперечная сила слева от сечения даёт отрицательный результат, то ордината силы Qy откладывается вниз.
Если сумма моментов сил, действующих на левую часть рамы, даёт равнодействующий момент, направленный по часовой стрелке, то ордината изгибающего момента в сечении откладывается вверх. Если же равнодействующий внешний момент слева от сечения направлен против хода часовой стрелки, то ордината изгибающего момента откладывается вниз.
Геометрические характеристики плоских фигур (статический момент площади, осевые моменты инерции, центробежный момент инерции, полярный момент инерции, радиус инерции). Их интегральные выражения. Статические моменты площади относительно центральных и нецентральных осей плоской фигуры.
 - статический момент площади фигуры относительно оси х.
- статический момент площади фигуры относительно оси х.
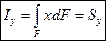 - статический момент площади фигуры относительно оси у.
- статический момент площади фигуры относительно оси у.
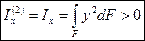 - осевой момент инерции относительно оси х.
- осевой момент инерции относительно оси х.
 - осевой момент инерции относительно оси у.
- осевой момент инерции относительно оси у.
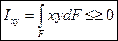 - центробежный момент инерции площади плоской фигуры относительно осей х, у.
- центробежный момент инерции площади плоской фигуры относительно осей х, у.
 - полярный момент инерции сечения.
- полярный момент инерции сечения.
 ,
,  .
.
 - статический момент площади относительно нецентральной оси х1 плоской фигуры.
- статический момент площади относительно нецентральной оси х1 плоской фигуры.
 - статический момент площади относительно нецентральной оси у1 плоской фигуры.
- статический момент площади относительно нецентральной оси у1 плоской фигуры.
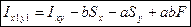 - центробежный момент инерции площади плоской фигуры относительно осей х1 и у1.
- центробежный момент инерции площади плоской фигуры относительно осей х1 и у1.
В случае центральных осей:  ,
,  ,
,  .
.
