Алгоритм реализация и решение системы дифференциальных уравнений

Реализация и решение системы дифференциальных уравнений описывающих динамическую систему позиционного гидропривода, в программе Matlab, выполнялось по следующему алгоритму:

1. Составление вычислительного блока для решения одномассовой матмодели позиционного гидропривода.

2. Введение в модель, подмодели гидравлического силового контура в составе которого участвуют гидрораспределители ВР, Р2 и Р3 с релейной схемой включения (учитывая реальное время срабатывания ^р=0,002.. Д003с) [2].

3. Введение в модель, подмодели гидравлического контура управления с гидролининиями связи - распределителя Р4, с квази-релейной схемой переключения.

4. Интеграцию в КГУ, модели гидравлического устройства управления - ГУКа, с аппроксимацией зависимости µ=f(x) соответствующей реальным гидродинамическим процессам, полученную с учетом динамических характеристик измерительных устройств [6].

5. Выбор метода решения системы дифференциальных уравнений математической модели и соответствующего размера шага.

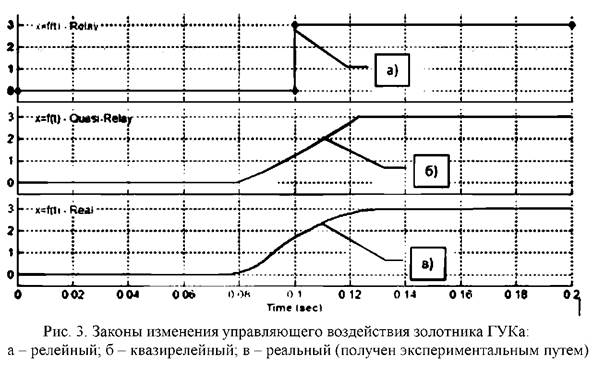
При решении дифференциальной системы уравнений, для исполнительного элемента КГУ - гидроуправляемого клапана, вначале использовались релейный (рисунок За), квази-релейный (рисунок Зб) и на завершающей стадии - реальный законы (рисунок Зв) перемещения управляющего элемента (золотника).

Таблица 1 - Параметры устройств КГУ

№ п/п	Параметры	Обозначе ние	Размер­ность	Диапазоны изменения
	Площадь проходного сечения распределителя	Sp	М2	0-0,0000785
	Коэффициент расхода распределителя	µз		0,8
	Проводимость управляющего распределителя	Кур		1Д3-10-4
	Жесткость пружины ГУКа	Спр	Н/м
	Предварительное натяжение пружины ГУКа	Х0	м	0,0095
	Давление контура гидравлического управления	Ру	Па	1,6-6,3-106
	Расход через ВР	Qвр	М3/с	0,0015-0,0138

Исходные данные, принятые для моделирования позиционного гидропривода приведены в таблице 2. Исследования проводились при различных диапазонах функционирования гидромеханической системы привода. Был определен базовый режим работы, характерный для большинства поворотно-делительных механизмов АТО.

В результате выполненной отладки и апробации вычислительных блоков программы, реализованной в подсистеме Simulink, получены осциллограммы зависимостей выходных параметров: φ, ω - механической подсистемы, а так же задающих воздействий- х_ГУК и x_P2, x_P4 - перемещения управляющих элементов КГУ.

Конфигурация интерфейса составленной программы позволила работать в диалоговом режиме, варьируя исходные данные (приведенные в Таблице 2), осуществлять выбор структуры задачи и мониторинг выходных характеристик. В ходе математического эксперимента, проводилась оценка погрешностей и статистическая обработка полученных численных данных по известной методике [7].

После каждого математического эксперимента, его результаты автоматически образовывали массив данных, со следующими параметрами:

Движение одномассовой механической подсистемы, характеризует фазовый портрет координаты перемещения выходного звена (рис.3). Движение приведенных масс /, в момент завершения процесса позиционирования, сопряжено с колебаниями (0,37 c), которые благодаря включению гидромеханического тормозного устройства - гасятся, в области Δφ.

Таблица 2 - Исходные данные для моделирования ПГП

№№	Параметры	Обозна	Размер-	Диапазоны	Базовый
п/п		чение	ность	изменения	режим
	Скорость	ωi	Рад./с	5-20
	Обобщенная сила сухого трения гидродвигателя	Мт01	Н·м	1-8	4,5
	Обобщенная сила гидро­механического тормоза	Мтз(t)	Н·м	10-100
	Основной конструктивный параметр гидродвигателя		м3/рад	3*10-6-25*10-6	5,57*10-6
	Коэффициент вязкого трения гидродвигателя	Ктм	Н·мс/рад	0,05-0,35	0,11
	Приведенный коэффициент жесткости	Cω	Н·м/рад	0-15000
	Перемещаемые ведущие массы	J1	кг м2	39*10-4-0,024	0,0034
	Приведенный момент инерции	Jп	Н·м·с2	0,01-0,1	0,033
	Давление насоса	Рн	Па	1,5*106-6,3*106	5,5*106
	Давление в сливой гидролинии	Рсл	Па	0,5*106-1,5*106	0,5*106