Дискретный метод Ньютона

Дискретный метод Ньютона базируется на аппроксимации матрицы Якоби на основе вычисленных значений функции 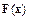в ряде вспомогательных точек. Построим его. Как и прежде, будем использовать векторную запись решаемой системы уравнений

.

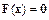Пусть известно k-е приближение 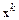к решению 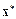. Аппроксимируем функцию 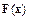линейной функцией:

.

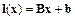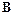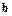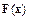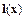Для численного определения матрицы и вектора потребуем, чтобы значения функций и совпадали в (n+1) вспомогательных точках 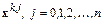, т. е. чтобы выполнялось равенство

.

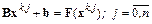Вычитая из первого равенства все последующие, получим соотношения

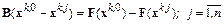
или в матричной форме

,

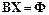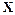где матрицы и 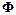имеют вид

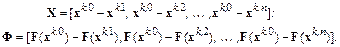
Следовательно,

.

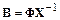Условие 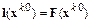позволяет найти вектор :

.

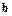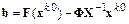Перепишем функцию 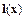, подставив найденные соотношения для 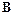и :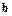

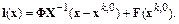
Примем 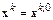. Будем искать 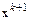из уравнения

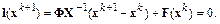
Получим итерационную формулу дискретного метода Ньютона:

.

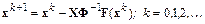Заменяя обращение матрицы решением линейной системы, придем к реализуемому на практике алгоритму дискретного метода Ньютона:

1. Вычисляется вектор 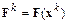, матрицы 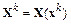и .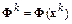

2. Решается система линейных алгебраических уравнений

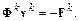
3. Вычисляется вектор поправки

.

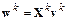4. Вычисляется (k+1)-е приближение

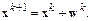
5. Пункты 1÷4 повторяются для k=0,1,2,… до получения решения с требуемой точностью.

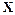Применение дискретного метода Ньютона предполагает хранение -матриц и 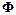. Однако на практике в качестве вектора 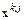выбирается вектор

,

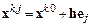где 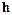– диагональная матрица параметров дискретизации, 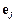– j-й столбец единичной матрицы. Элементы 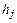матрицы 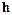вычисляют по правилу 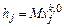, где 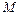– константа (например, 0.1).

Часть 4. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ

Лекция 7

Полиномиальная интерполяция

ЦЕЛЬ ЛЕКЦИИ: Пояснить сущность задачи интерполяции; дать общую схему ее решения; построить интерполяционный полином Лагранжа, ввести разделенные разности и получить на их основе интерполяционный многочлен Ньютона.

Постановка задачи.

Важным элементом численного анализа является задача интерполирования функций, которую приходится решать в следующих приложениях: машинная графика, автоматизация проектирования, обработка экспериментальных данных, управление, передача данных и др. При этом часто возникает задача восстановления функции на отрезке, если известны ее значения в конечном числе точек отрезка. Эти значения определяются на основании экспериментальных измерений либо в результате вычислений.

Сформулируем математическую постановку задачи интерполяции.

Пусть на отрезке 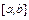в точках

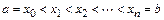
известны значения функции 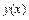, равные

.

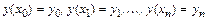Требуется построить интерполянту – интерполяционную функцию 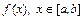, совпадающую с функцией 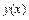в точках :

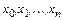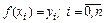(7.1)

и в то же время аппроксимирующую ее, естественно приближенно, на всем отрезке .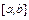

Основной вопрос интерполяции: как выбрать интерполянту 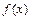и как оценить погрешность 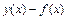? Интерполяционные функции строятся, как правило, в виде линейной комбинации некоторых линейно-независимых элементарных функций :

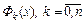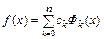, (7.2)

где 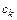– коэффициенты, которые можно определить, используя условие (7.1). Из этого условия

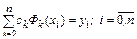. (7.3)

Относительно коэффициентов 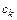получили систему линейных алгебраических уравнений, порядок которой равен n+1. В силу линейной независимости элементарных функций 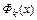определитель этой системы отличен от нуля, и решение для 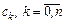единственно. Таким образом, вычисляя 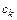из (7.3) и подставляя их в (7.2), можем получить значение 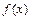в любой точке .

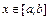В качестве системы линейно-независимых функций 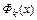чаще всего выбирают степенные функции, например 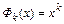. В этом случае 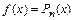– полином степени n.