Температурное поле ПТИ в полубесконечном теле

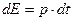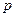Точечный источник теплоты, действующий постоянно имеет постоянную мощность, площадь воздействия источника стремится к нулю, поток энергии бесконечен. Суммарная энергия, поступающая в тело, линейно возрастает. Температурное поле ПТИ может быть найдено суммированием по времени температурных полей мгновенных точечных источников с энергией: , где - мощность источника. Температурное поле имеет центральную симметрию, изометрические поверхности в полубосконечном теле – полусферы с радиусом 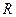. Граничную поверхность тела будем считать адиабатическойб, ось 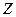направлена внутрь тела.

В этом случае приращение температуры выразится формулой:

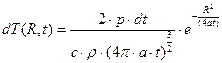(1)

Интегрирование (1) в пределах от нуля до текущего времени 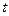для полубесконечного тела даёт:

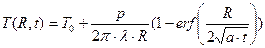(2)

Интегрирование осуществляется с помощью замены переменных: 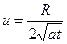, которая сводит (1) к интегралу вероятности Гаусса: 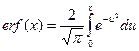. Функция 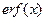нечётна, причём 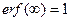. В системе MatLab имеются специальные, встроенные подпрограммы-функции для вычисления 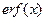и 1- 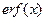с именам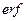и и 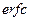соответственно. Функция 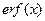быстро возрастает и уже .

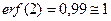В точке воздействия температура бесконечна, с увеличением расстояния 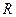быстро уменьшается. Градиент температуры направлен вдоль радиуса и уменьшается с течением времени. При 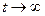, температура в точке 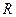стремится к постоянному, предельному значению:

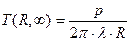(3)

Эта температура называется температурой предельного состояния - 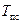. Температура предельного состояния обратно пропорциональна расстоянию от источника. В предельном состоянии тепловой поток через изотермическую поверхность радиуса 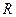не зависит от радиуса и равен интенсивности источника.

Составим подпрограмму расчёта зависимости температуры от времени для заданного расстояния от точки воздействия:

function [T,Tp,Ts]=Tppdin(pt,p,R,m)

%Temper pole T - postoiannogo istochnika dlia zadannogo R.

v=mview(m);

eval(v)

T0=20;

Tp=p./(la*2*pi*R);

T=T0+Tp.*erfc(R./(2.*sqrt(pt.*at)));

n=length(pt);

Tp(1:n)=Tp;

Ts=(0.15*p/(ce*ro*R^3))*pt-0.01*p/(la*R);

Входные параметры подпрограммы:

pt – вектор, задающий множество моментов времени;

p – мощность источника [Вт];

R – расстояние от точки воздействия [см];

m – имя материала.

Выходные параметры: T – вектор температур, Tp – вектор температур предельного состояния, Ts – вектор температур аппроксимирующей прямой.

Вызов программы:

p=1000;m='Cu';

>> v=mview(m);

>> eval(v)

>> R=p/(2*pi*la*Tpl)

R =0.0382

>> pt=R^2/at

pt = 0.0016

>> pt=[0.000001:0.000001:0.002];

>> [T,Tp,Ts]=Tppdin(pt,p,R,m);

>> plot(pt,T,pt,Tp,pt,Ts); grid on;

Параметры R и pt выбраны так, что температура предельного состояния соответствует температуре плавления меди. Кривая температуры имеет точку перегиба, совпадающую с максимумом подынтегрального выражения при 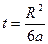, при этом приращение температуры:

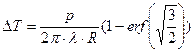
Угол наклона касательной к кривой температуры в точке перегиба равен значению подынтегрального выражения в точке 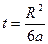: 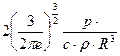. Уравнение касательной к кривой температуры после подстановки констант приближённо имеет вид:

.

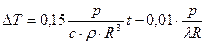Касательная пересекает ось времени в точке 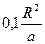и прямую соответствующую температуре предельного состояния при .

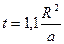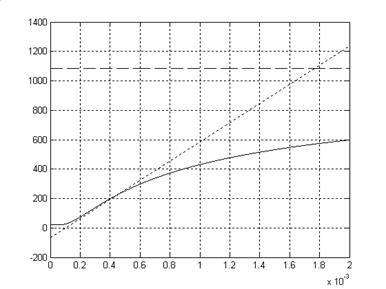
Рис. 5

На рис. 5 показаны зависимости температуры от времени в точке 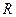, штриховой линией показана температура предельного состояния, пунктиром касательная.

В точке 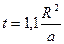значение температуры составляет примерно 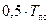. Это может быть использовано для автоматического выбора масштаба в программе расчёта зависимости температуры от времени для заданного набора расстояний от точки воздействия. Например, начальное значение временного интервала можно положить равным: 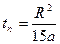, а конечное: 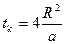, при этом все характерные участки кривой температуры попадут на график.

Ниже приведена программа расчёта зависимости температуры от времени для набора расстояний до точки воздействия. Для расчёта температуры использована подпрограмма Tppdi, аналогичная Tppdin, но с одним выходным параметром (8-10 строки подпрограммы исключены).

function [pt,T]=TppdiR(p,R,m)

%Temper pole T - postoiannogo istochnika dlia semeistva R.

T=[];

v=mview(m);

eval(v)

n=length(R);

Rmi=min(R);

Rma=max(R);

tn=Rmi^2/(10*at);

tk=4*(Rma^2/at);

sht=(tk-tn)/100;

pt=[tn:sht:tk];

for i=1:n

Rv=R(i);

Tv=Tppdi(pt,p,Rv,m);

T=[T;Tv];

end

T=T';

Здесь R – вектор, содержащий набор расстояний до точки воздействия, а pt – вектор моментов времени. Вызов программы:

>> p=1000;m=’Cu’;R=[0.02:0.002:0.026];

>> [pt,T]=TppdiR(p,R,m);

>> plot (pt,T); grid on;

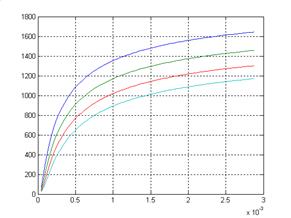
Рис. 6

На рисунке 6 показано семейство кривых для набора расстояний до точки воздействия. В конечной точке временного интервала 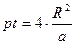значение температуры составляет: .

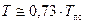Для каждого значения температуры существует расстояние от точки воздействия, для которого эта температура является предельной. Это расстояние может быть найдено из формулы (3). Так, если принять, в качестве температуры предельного состояния температуру плавления получим:

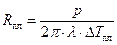(4)

За время: 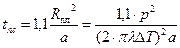будет достигнуто половинное значение температуры плавления на этом расстоянии. При заданной мощности источника, радиус изотермы плавления не достигнет значения 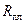за любое конечное время.

Если зафиксировать момент времени и изменять расстояние, из (2) можно получить зависимость температуры от расстояния. Для этого может быть использована та же подпрограмма Tppdi, что и в предыдущем случае, но переменная, задающая время не должна быть вектором, а переменная R, должна содержать набор значений расстояния до точки воздействия, в которых происходит вычисление температуры. Программа получения семейства зависимостей T(R) получается из программы TppdiR путем незначительной модификации:

function [R,T]=TppdiT(p,t,m)

%Temper pole T(R) - postoiannogo istochnika dlia semeistva t.

T=[];

v=mview(m);

eval(v)

n=length(t);

tmi=min(t);

tma=max(t);

Rn=((tmi*at)^0.5)/2;

Rk=4*((tma*at)^0.5);

shR=(Rk-Rn)/100;

R=[Rn:shR:Rk];

for i=1:n

Tv=Tppdi(t(i),p,R,m);

T=[T;Tv];

end

T=T';

Вызов подпрограммы:

>> p=1000; m=’Cu’; t=[0.001:0.002:0.007];

>> [R,T]=TppdiT(p,R,m);

>> plot (R,T); grid on;

Результаты счёта приведены на рисунке 7.

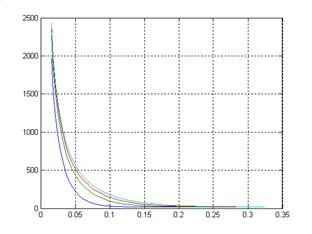
Рис.7

Как следует из рисунка 7, температура в каждой точке тела с течением времени нарастает с некоторым замедлением.

Если заданы температура 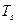и время, положение изотермы 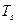можно найти, решив уравнение (2) относительно 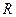. Решить это уравнение можно только с помощью численных методов. Ниже приведена программа нахождения положения изотермы с температурой 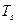в момент времени :

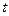function R=TpdiRs(t,p,Ts,m)

%pologenie Rs izotermi Ts PDI: moshnost-p, vremia-t.

v=mview(m);

eval(v)

dT=Ts-20;

Rp=p/(2*pi*la*dT);

pt=((100*Rp)^2)/at;

if t>=pt

R=Rp;

else

Rl=((at*t)^(1/2))/20; вычисление начального значения левого конца отрезка аргумента;

Tl=Tppdi(t,p,Rl,m);

while Tl<Ts

Rl=Rl/2;

Tl=Tppdi(t,p,Rl,m);

end

Rr=20*(at*t)^(1/2);

Tr=Tppdi(t,p,Rr,m); вычисление начального значения правого конца отрезка аргумента;

while Tr>Ts

Rr=Rr*2;

Tr=Tppdi(t,p,Rr,m);

end

mT=Ts-20;

while abs(mT)>1 цикл деления отрезка аргумента пополам;

Rm=(Rr+Rl)/2;

Tm=Tppdi(t,p,Rm,m);

mT=Tm-Ts;

if mT>0

Rl=Rm;

else

Rr=Rm;

end

end конец цикла дихотомии;

end

R=Rm;

Входными параметрами являются: значение момента времени - 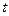[c], мощность источника - 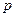[Вт], температура изотермы - 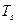, и имя материала. Выходной параметр – радиус изотермы- 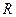[см]. Вызов подпрограммы:

>> t=0.1;p=1000;Ts=1080;m='Cu';

>> R=TpdiRs(t,p,Ts,m)

R =0.0364

Уравнение (2) в подпрограмме решается методом дихотомии (деления пополам).

Программа отыскивает значение температуры T, при которой обращается в ноль функция: Y=T(R,t)-Ts. Эта функция, рассчитанная для фиксированного момента времени t=0.0001 приведена на рисунке 8.

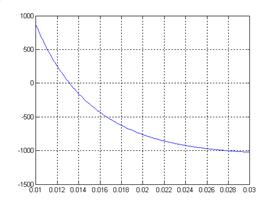
Рис.8

Для того, что бы найти корень уравнения необходимо задать интервал значений R, содержащий корень (на рис. 8 - 0.01-0.03см) и точность, с которой этот корень должен быть найден. В приведённой программе концы интервала находятся автоматически, а точность составляет один градус. Суть метода дихотомии заключается в том, что если значение некоторой функции обращается в ноль в единственной внутренней точке интервала аргумента, то на концах этого интервала значения функции имеют разные знаки. Если вычислить температуру в центральной точке интервала аргумента (на рисунке точка 0.02см), то значения функции на концах для левой половины интервала будут иметь разные знаки, а для правой одинаковые. Для продолжения поиска следует выбрать левую половину интервала и процедуру повторить. Вычисления продолжаются до тех пор, пока значение функции в центральной точке интервала не станет меньше заданного, при этом на каждом шаге выбирается половинка интервала аргумента с различными знаками значений функции на концах.

Если задать множество моментов времени, и в каждый момент вычислить положение изотермы, то будет получена зависимость положения заданной изотермы от времени. Это можно сделать с помощью специальной программы:

function R=TpRTst(t,p,Ts,m)

%zavisimost pologenia R izotermi Ts ot vremeni-t PDI: moshnost-p,vektor vremeni-t.

v=mview(m);

eval(v)

n=length(t); определение количества элементов в векторе t;

for i=1:n;

R(i)=TpdiRs(t(i),p,Ts,m);

end

Вызов подпрограммы:

>> p=1000;m='Cu';v=mview(m);eval(v);Ts=Tpl;

>> t=[0.0001:0.0001:0.01];

>> R=TpRTst(t,p,Ts,m);

>> Ts=Tkp; R1=TpRTst(t,p,Ts,m);

>> plot (t,R,'k-',t,R1,'k:'); grid on;

>> legend('plavl','kipen')

>> ylabel('paccm(cm)')

>> xlabel('vrem(c)')

>> title('RTs(t)')

Вычисления проведены для двух значений температуры: температуры плавления и температуры кипения. Результаты приведены на рис. 7:

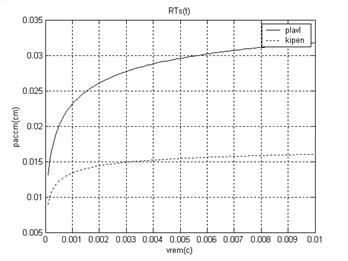
Рис. 7

Как следует из рисунка, с течением времени движение изотерм замедляется, и их положение стремится к предельным значениям (формула (4)).