Итерационные методы решения обратной задачи структурной гравиметрии на экстремальных классах

В ситуациях, когда поле задано на рельефе и на нерегулярной сети наблюдений, образующей уже введенное ранее множество , применение спектральных методов ограничено. Следует использовать прямые методы вычислений по аналогии с тем, как это было сделано для задачи о распределении плотности. С этой целью воспользуемся характеристикой экстремальных классов :

(7.106)

В операторной форме она записывается следующим, сокращенным образом:

.

(7.107)

В частности, можно так подобрать операторы , что ,

где положительно определенные, самосопряженные операторы. В этом случае (107) оказывается эквивалентным (76), если . Будем считать, что в окрестности решения оператор имеет область значений не меняющуюся при изменении . Это будет выполнено, в частности, если регулярен в окрестности .

В этом случае, для выделения решения уравнения

на экстремальном классе (107) можно воспользоваться результатами 5.6.2. Итерационный процесс, доставляющий решение будет выглядеть следующим образом:

(7.108)

Здесь оператор 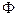имеет смысл трансформации интерпретируемой компоненты поля, для наиболее рельефной компенсации невязки. Например, это может быть комбинация единичного оператора и оператора дифференцирования вплоть до заданного порядка. В этом случае, будет обеспечена не только компенсация невязки, но и компенсация производных поля. Если в качестве 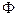выбрать умножение на весовую функцию, то это будет соответствовать компенсации поля с учетом весов, отражающих, например, сравнительную меру достоверности различных участков поля. Выбор параметра релаксации , обеспечивающего сходимость процесса, осуществляется по формуле:

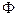- сопряженный к оператор.

Наряду с формулой (108) для выбора параметра релаксации, следующей из принципа минимальных невязок, может быть использован прямой подбор оптимального параметра для пошаговой минимизации величины:

(7.109)

Рассчитывая величину для различных значений параметра релаксации можно оценить оптимальное значение путем аппроксимации зависимости по нескольким рассчитанным точкам. Такой прием оправдан в ситуациях, когда наряду с итерационным процессом (108) осуществляется дополнительная «правка» получаемого приближения. Она может осуществляться за счет имеющихся ограничений на глубины залегания границ в разных точках, условий взаимосвязи и взаимообусловленности положения границ, выходящие за рамки процедуры (108). Если обозначить - множество, которому должны принадлежать границы дополнительно ко всему тому, что было уже введено, то учет всех ограничений сводиться к проектированию на . Сюда относится и требование чтобы границы обладали некоторыми свойствами - например, взаимосвязи и обусловленности. Тогда учет этих факторов приводит к модифицированному процессу:

(7.110)

Здесь - операция проектирования в норме пространства (например, границ ) на множество . Собственно, в качестве может выступать любое отображение из на . Именно в таком модифицированном итерационном процессе оказывается актуальным процедура прямого подбора параметра релаксации, обеспечивающего минимизацию величины.

(7.111)