Формы и методы контроля и оценки результатов обучения

Вычисление двойных интегралов

Методические указания к самостоятельной работе студента 19

Учебная дисциплина: Элементы высшей математики

Модуль: ЕН.01.М.07 Функции нескольких переменных

Учебный элемент: УЭ.07.02 Интегральное исчисление функции двух переменных

Специальность: 230115 Программирование в компьютерных системах

Разработал:

Г.К.Болотова

Цели

1.1 В ходе выполнения работы студенты осваивают:

1.1.1 Общие компетенции, включающие в себя способность:

ОК 2 Организовывать собственную деятельность, выбирать типовые методы и

способы выполнения поставленных задач, оценивать их эффективность и качество

ОК 3 Принимать решения в стандартных и нестандартных ситуациях и уметь их обосновывать

ОК 4 Осуществлять поиск и использование информации, необходимой для эффективного выполнения поставленных задач, профессионального и личностного развития

ОК 8 Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием

1.2 В результате выполнения работы студенты:

1.2.1 Осваивают умения:

- анализировать область интегрирования, подынтегральную функцию, выбирать формулу интегрирования;

- сводить двойной интеграл к повторным интегралам;

- находить первообразные подынтегральных функций, применять формулу Ньютона - Лейбница

1.2.3 Усваивают знания:

- формул вычисления двойных интегралов;

- алгоритма сведения двойных интегралов к повторным

Дидактическое обеспечение

2.1 Учебные пособия (УП):

- УП.1 Бермант, А.Ф. Краткий курс математического анализа: Учеб. Пособие/ Бермант А.Ф., Араманович И.Г. – 8-е изд., стер. – М.: Наука, 1973. – 720с.: ил.

- УП.2 Подольский, В.А. Сборник задач по математике: Учеб. пособие/Подольский В.А., Суходский А.М., Мироненко Е.С. – 3-е изд., стер. – М.: Высш.шк., 2005. – 495 с.: ил.

2.2 Сравнительная таблица определенного и двойного интегралов (Приложение А)

2.3 Индивидуальное практическое задание 19 (ИПЗ.19, приложение Б))

2.4 Методические рекомендации по выполнению ИПЗ.19

2.5 Правила вычисления двойных интегралов (Приложение В)

3 Форма организации –индивидуальная

Инструктаж

4.1 Для усвоения и систематизации базовых знаний и умений следует использовать:

- конспект лекций;

- дидактическое обеспечение учебного элемента УЭ.07.02

4.2 Задания, предусмотренные для закрепления базовых умений и знаний, выполняются в рабочем конспекте лекций

4.3 Вариант ИПЗ.19 выбирается согласно номеру в списочном составе группы по журналу учебных занятий

4.4 ИПЗ.1 9 выполняется в тетради для самостоятельной работы студента и сдается на проверку преподавателю в установленный срок

4.5 Время выполнения:

- изучение теоретического материала - 2 часа;

- выполнение ИПЗ.19 - 2 часа

Порядок выполнения

5.1 Ознакомиться с содержанием таблицы 1 Структура учебного элемента УЭ.07.02

Таблица 1 Структура учебного элемента 07.02

Наименование модуля, учебного элемента (УЭ)	ЕН.01.07 Функции нескольких переменных
УЭ.07.02 Интегральное исчисление функции двух переменных
Освоение УЭ	Количество часов
Теоретическое обучение	Практические занятия	самостоятельная работа студента
Учебные занятия	Самостоятельная работа студента
Содержание задания	Вид деятельности
102 Задачи, приводящие к понятию двойного интеграла. Определение двойного интеграла, основные свойства	УП.1 Гл.VIII,§ 1, п.128, 129 УП.2 Гл.15,§ 9 (с.365)	1 Заполните сравнительную таблицу, приложение В 2 Подготовьтесь: - к опросу по правой части сравнитель-ной таблицы; - к контролю по алгоритму вычисления объем цилиндрического тела
103 Формулы вычисления двойного интеграла. Повторные интегралы	УП.1 Гл.VIII,§ 1, п.130 УП.2 Гл.15,§ 9 (с.366-369), № 15.195,15.198	1 Выучите формулы вычисления двойного интеграла 2 Закрепите базовые умения: - проанализируйте решение задач: № 15.182-15.184 - выполните: № 15.195,15.198
104 Сведение двойных интегралов к повторным. Вычисление двойных интегралов	УП.2 Гл.15,§ 9, № 15.215,15.216, ИПЗ.19 – задания 1,2	Закрепите базовые умения: - проанализируйте решение задачи: № 15.185 - выполните: № 15.215,15.216 ИПЗ.19 – задания 1,2
105 Вычисление площади плоской области и объемов тел с помощью двойного интеграла	УП.2 Гл.15,§ 11, №15.239,15.240, ИПЗ.19 – задание 3	Закрепите базовые умения: - проанализируйте решение задачи: № 15.235 - выполните: №15.239,15.240 ИПЗ.19 – задание 3
106 Практическое занятие 22 Вычисление двойных интегралов	Методические указания к практическому занятию 22	Подготовьте к сдаче ИПЗ.19

5.2 Закрепить материал соответствующего учебного занятия, выполнить указанные виды деятельности

5.3 Ознакомиться с содержанием ИПЗ.19

5.4 Ознакомиться с методическими рекомендациями по выполнению ИПЗ.19

Методические рекомендации

6.1 Рассмотрите правила вычисления двойных интегралов (приложение В)

6.2 При выполнении задания 1 следует:

1⁰ Проанализировать постановку задачи, установить по какой формуле записан повторный интеграл А или В

2⁰ Записать уравнения линий, ограничивающих область D

3⁰ Построить область D

4⁰ Если данный повторный интеграл был записан по формуле А, то рассмотреть проекцию области D на ось ОУ и записать его по формуле В. Если данный повторный интеграл был записан по формуле В, то рассмотреть проекцию области D на ось ОХ и записать его по формуле А

6.3 При выполнении задания 2 следует использовать формулу А

6.4 При выполнении задания 3 следует использовать формулу В

Формы и методы контроля и оценки результатов обучения

7.1 Текущий контроль по учебным занятиям

7.2 Тестовый контроль выходе

7.3 Выполнение и оценка ИПЗ.19

8Критерии оценок

8.1При контроле и оценки усвоения базовых знаний учитывается:

- точность воспроизведения основных понятий, определений, характеристик изучаемых объектов;

- правильность записи основных формул, правил необходимых для решения задач

8.2 При контроле и оценки освоения базовых умений учитывается:

-правильность анализа поставленной задачи;

- выбор метода и формулы сведения двойного интеграла к повторным;

- выбор формул интегрирования повторных интегралов

- соответствие полученных результатов эталону ответа

8.3 Оценка выполнения ИПЗ.19:

- «Отлично» - выполнен полный объём заданий в соответствии с п.8.2;

- «Хорошо» - выполнен полный объём заданий в соответствии с п.8.2, но в одном из заданий допущены вычислительные ошибки;

- «Удовлетворительно» - выполнен полный объём заданий в соответствии с п.8.2, но в заданиях допущены вычислительные ошибки;

- «Неудовлетворительно» - студентом не реализованы цели данной работы, выполненные задания не соответствуют п.8.2

Приложение Б

Содержание индивидуального практического задания

Задание 1Измените порядок интегрирования

1.1		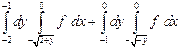1.13	+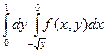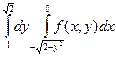
1.2		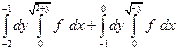1.14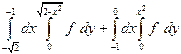
1.3		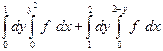1.15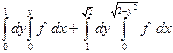
1.4		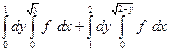1.16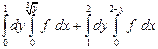
1.5		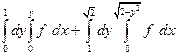1.17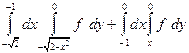
1.6		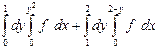1.18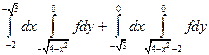
1.7		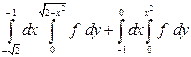1.19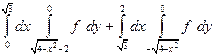
1.8		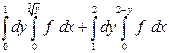1.20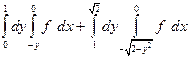
1.9		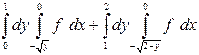1.21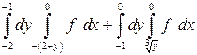
1.10		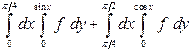1.22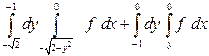
1.11		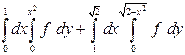1.23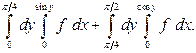

Приложение Б

(продолжение)

1.1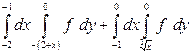

1.24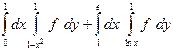

Задание 2Вычислите двойные интегралы по областям, ограниченным указанными линиями

2.1		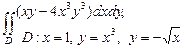2.13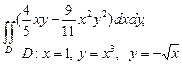
2.2		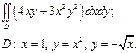2.14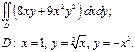
2.3		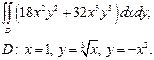2.15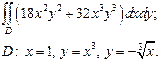
2.4		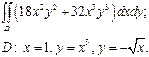2.16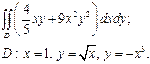
2.5		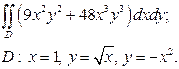2.17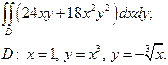
2.6		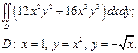2.18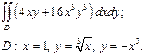
2.7		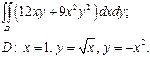2.19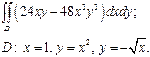
2.8		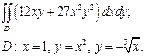2.20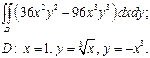
2.9		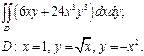2.21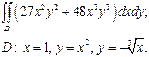

Приложение Б

(продолжение)

2.10		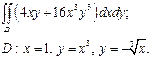2.22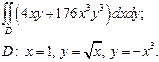
2.11		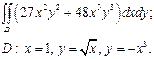2.23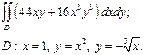
2.12		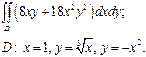2.24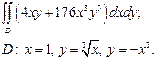

Задание 3 Вычислите двойные интегралы по областям, ограниченным указанными линиями

3.1		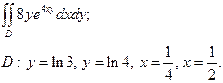3.13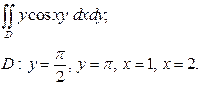
3.2		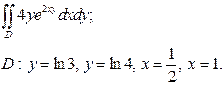3.14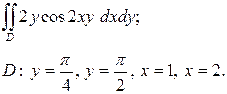
3.3		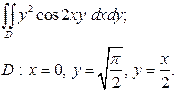3.15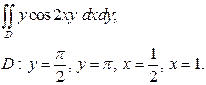
3.4		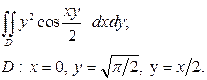3.16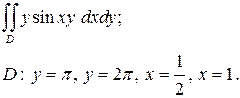
3.5		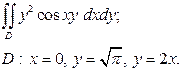3.17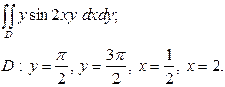

Приложение Б

(окончание)

3.6		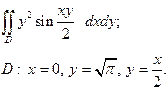3.18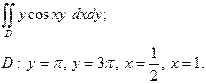
3.7		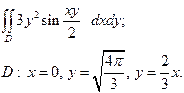3.19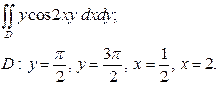
3.8		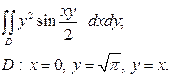3.20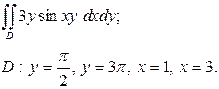
3.9		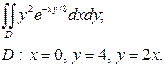3.21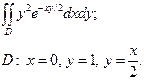
3.10		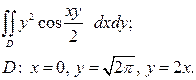3.22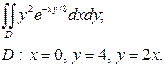
3.11		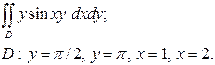3.23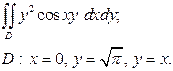
3.12		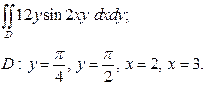3.24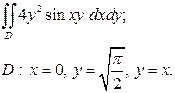

Приложение В

Правила вычисления двойных интегралов

Различают два основных вида области интегрирования.

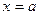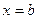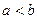Область интегрирования D ограничена слева и справа прямыми и ( ), а снизу и сверху – непрерывными кривым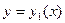и и 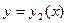( 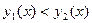), каждая из которых пересекается вертикальной прямой на интервале 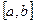в одной точке (рис.1)

y

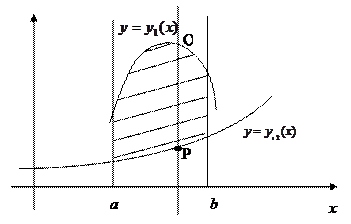
Рис. 1

При интегрировании такая область проектируется на ось ОХ и определяются пределы интегрирования 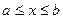. Точку Р называют точкой «входа», точку Q – точкой «выхода» (рис.1). По уравнениям линий на которых лежат точки P и Q определяются пределы интегрирования внутреннего интервала

Для такой области двойной интеграл вычисляется по формуле

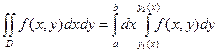(А)

причём сначала вычисляется внутренний интеграл 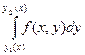, в котором х считается постоянным.

Область интегрирования D ограничена снизу и сверху 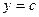и 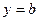( 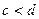), а слева и справа – непрерывными кривым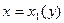и и 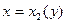( 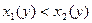) , каждая из которых пересекается горизонтальной прямой на интервале 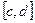только в одной точке (рис. 2)

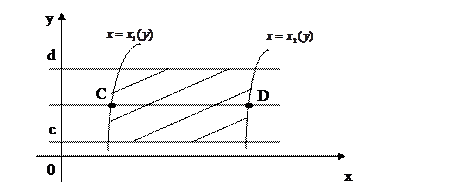
Рис. 2

Приложение В

(окончание)

Область D проектируется на ось ОУ и определяются пределы интегрирования внутреннего интеграла 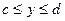. По точкам С и D аналогично определяются границы внутреннего интеграла. В этом случае х выражается через у

Для такой области двойной интеграл вычисляется по формуле

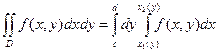(B),

причём сначала считается внутренний интервал 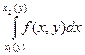, в котором y считается постоянным.

Правые части указанных формул называются двукратными (или повторными) интегралами.

Если область интегрирования на интервале 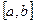или 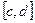(рис.3) ограничена графиками двух или более функций, то двойной интеграл разбивается на сумму двух или более повторных интегралов.

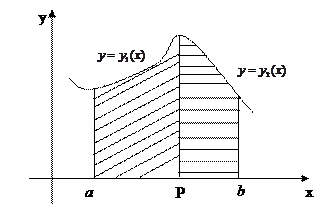
Рис. 3

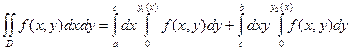
Обратите внимание

При выборе формулы (А) или (В) анализируется:

- область интегрирования D, чтобы избежать разбиения двойного интеграла на сумму повторных;

- подынтегральная функция, чтобы проще вычислять внутренний интеграл.