Методы построения математических моделей

Математические модели стационарных режимов

Электрических цепей

В электротехнике часто встречается задача расчета ли­нейных электрических цепей. Математической моделью таких цепей является система алгебраических уравнений, основан­ных на законах Кирхгофа. Для анализа математических моделей стационарных режимов электрических цепей широко применяются методы контурных токов и узловых потенциа­лов. Эти методы подробно изучаются в курсе “Теоретические основы электротехники”. В настоящем курсе остановимся на применении ЭВМ для расчетов электрических цепей.

Они основаны на применении матричных методов. Топо­логия электрической цепи описывается в виде топологичес­ких матриц, описывающих связи, например, между контура­ми. В итоге, модель сводится к системе линейных уравнений, в которой число уравнений равно числу неизвестных. Такую систему можно записать в матричном виде:

AI=U, (1)

где A=[a _kj] — квадратная матрица коэффициентов при не­известных токах.

I = [i _j] —вектор столбец неизвестных токов,

U =[u _к] —вектор столбец источников ЭДС ветвей.

Вопросы для самопроверки

1. Что называется матрицей?

2. Какие виды матриц используются при проведении технических расчётов?

3. Какие варианты решений возникают при решении систем линейных уравнений?

4. Какую математическую форму имеет модель линейной электрической цепи?

Численное решение системы линейных уравнений

Для численного решения системы линейных уравнений обычно применяются алгоритмы, являющиеся модификация­ми метода Гаусса.

Методом Гаусса называют точный метод решения невы­рожденной системы линейных уравнений, состоящий в том, что последовательным исключением неизвестных систему:

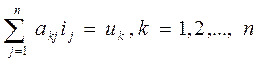(2)

приводят к эквивалентной системе с треугольной матрицей,

i₁ + c₁₂ i₂ + c₁₃ l₃ + c_1n i _n = v ₁

i₂ + c₂₃ i₃ + … + c_2n i _n = v ₂ (3)

i _n = v _n,

решение которой находят по рекурентным формулам

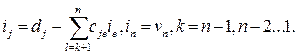(4)

Одной из модификаций метода Гаусса является схема с выбором главного элемента. Пусть исходная система имеет вид

a₁₁ i₁ + … + a_n i_n = u₁,

a₂₁ i₁ + … + a_2n i_n = u₂,

a_n1 i₁ + … + a_nn i_n = u_n,

Предположим, что а₁₁¹0 и разделим обе части первого уравнения системы на а₁₁. В результате получим

i₁ + c₁₂ i₂ + … + c_1n i _n = v ₁, (6)

где c_1j = a_1j/a₁₁, j = 2, 3, … n

v₁ = u₁/a₁₁.

С помощью полученного уравнения исключаем из всех остальных уравнений системы члены, содержащие i₁. После чего получим систему, порядок которой на единицу меньше, чем исходный

a¢₂₂i₂ + … + a¢_2ni_n = u¢₂ (7)

a¢_2ni₂ + … + a¢_nni_n = u¢_n,

где a¢_kj = a_kj - a_kl a_lj, i, j = 2, 3, … n

u¢_k = u_k - a_kl× u₁, k = 2, 3, … n.

Повторяя описанные преобразования, получим систему с треугольной матрицей (3).

Полученная система эквивалента исходной, но решать её легко. В самом деле, из последнего уравнения находим i_n, подставляя его в предпоследнее — найдем i_n-1 и т. д.

Вычисления по методу Гаусса выполняются в два этапа.

Первый этап называется прямым ходом метода. На первом этапе исходную систему преобразуют к треугольному виду. Второй этап называется обратным ходом. На втором этапе решают треугольную систему, эквивалентную исходной.

Коэффициенты а₁₁, а_22, …, называют ведущими элементами. На каждом шаге предполагалось, что ведущий элемент отличен от нуля. Если это не так, то в качестве ведущего можно использовать любой другой элемент, как бы переста­вив уравнения системы (5).

Особенностью численного счета является возникновение погрешностей округления. Так если k-ый ведущий элемент мал, то при делении на него и вычитания k-го уравнения из последующих, возникают большие погрешности округления.

Особенностью метода Гаусса с выбором главного элемента является такая перестановка уравнений, чтобы на k-ом шаге ведущим элементом оказывался наибольший по модулю элемент k-го столбца.

Фрагмент программы на языке Бейсик, реализующий опи­санный метод приведен в приложении Б.

Вопросы для самопроверки

1. В чем состоит метод Гаусса решения системы линей­ных уравнений?

2. Какие преобразования выполняются при прямом ходе метода?

3. Какие преобразования выполняются при обратном ходе метода?

4. Какая система линейных алгебраических уравнений называется невырожденной?

5. В чем особенность метода Гаусса с выбором главного элемента?