Проектирование и исследование динамической нагруженности двс большегрузного автомобиля
Глава 1. Исходные данные для проектирования. 6
Глава 2. Блок-схема исследования динамики машинного агрегата. 9
Глава 3. Динамический синтез и анализ машинного агрегата. 11
Пункт 3.1. Задачи динамического синтеза и анализа. 11
Пункт 3.2. Структурный анализ исполнительного рычажного механизма. 11
Пункт 3.3 Определение основных размеров, масс и моментов инерции звеньев. 12
Пункт 3.4 Построение 12 планов положения механизма. 15
Пункт 3.5 Кинематический анализ механизма. 15
Подпункт 3.5.1 Графический метод кинематического анализа. 15
Подпункт 3.5.2 Аналитический метод расчета. 16
Пункт 3.6 Определение сил движущих действующих на поршень. 18
Пункт 3.7 Динамическая модель машинного агрегата. 19
Пункт 3.8 Определение приведенных моментов сил движущих и сил сопротивления. 20
Пункт 3.9 Определение переменной составляющей приведенного момента инерции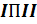 
22
Пункт 3.10 Определение постоянной составляющей приведенного момента инерции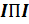 
и момента инерции маховика 
.. 23
Пункт 3.11 Определение закона вращения звена приведения. 24
Пункт 3.12 Схема алгоритма программы исследования динамической нагруженности машинного агрегата. 25
Пункт 3.13. Обработка результатов расчётов. 29
Пункт 3.14. Выводы.. 34
Глава 4. Динамический анализ рычажного механизма. 35
Пункт 4.1. Задачи динамического анализа. 35
Пункт 4.2. Кинематический анализ механизма. 35
Подпункт 4.2.1. Графический метод расчётов. 35
Подпункт 4.2.2. Аналитический метод расчётов. 37
Подпункт 4.2.3. Сопоставление расчётов. 38
Пункт 4.3. Силовой расчёт. 38
Подпункт 4.3.1. Графический метод расчётов. 39
Подпункт 4.3.2. Аналитический метод. 40
Пункт 4.4. Обработка результатов расчётов. 43
Пункт 4.5. Выводы.. 45
Глава 5. Синтез кулачковых механизмов. 46
Пункт 5.1. Задачи синтеза. 46
Пункт 5.2. Исходные данные для проектирования. 46
Пункт 5.3. Определение кинематических характеристик. 47
Пункт 5.4. Определение основных размеров кулачкового механизма. 48
Пункт 5.5. Определение координат центрового профиля кулачка. 50
Пункт 5.6. Построение графиков кинематических характеристик. 51
Пункт 5.7. Построение графика угла давления. 53
Пункт 5.8. Построение полной и упрощённой совмещённых диаграмм 
53
Пункт 5.9. Построение центрового профиля кулачка. 53
Пункт 5.10. Определение радиуса ролика и построение действительного профиля кулачка. 54
Пункт 5.11. Определение жёсткости замыкающей пружины.. 55
Пункт 5.12. Выводы.. 55
Литература. 57
Глава 1. Исходные данные для проектирования
ПРОЕКТИРОВАНИЕ И ИССЛЕДОВАНИЕ ДИНАМИЧЕСКОЙ НАГРУЖЕННОСТИ ДВС БОЛЬШЕГРУЗНОГО АВТОМОБИЛЯ
Механизм движения автомобиля состоит из двигателя, коробки передач, карданного вала и ведущего моста.
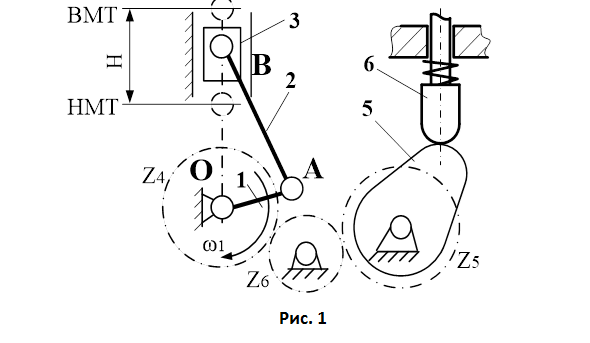
Двигатель внутреннего сгорания – двухтактный одноцилиндровый с вертикальным расположением цилиндра, представляет собой центральный четырехзвенный кривошипно-ползунный механизм (рис. 1). Движение передается от поршня 3 через шатун 2 на кривошип 1. Характер изменения давления в цилиндре в зависимости от перемещения хода поршня 3 показан на индикаторной диаграмме (рис. 2).
Через зубчатую передачу Z4Z5 движение от коленчатого вала двигателя передается распределительному валу механизма газораспределения и подачи топлива, на котором закреплен кулачок 6. На рис. 1 показана схема кулачкового механизма привода клапанов с поступательно движущимся роликовым толкателем 7. Закон движения толкателя на фазе удаления и возвращения – параболический несимметричный, коэффициент несимметричности ν = а1/а2 указан в Приложении.
Для всех вариантов принять:
1. Массы звеньев:
m2 = q·lАВ, m3 = 0,65m2 , m1 = 6m2 ,
где q = 15 кг/м.
2. Моменты инерции шатуна 2 и кривошипа 1:
, 
.
3. Фазовые углы кулачка:
φу = φв , φд.с. = 150 .
4. Центры масс звеньев:
lOS1 = 0 , lAS2=0,35lAB .
5. Масса толкателя кулачкового механизма – 500 г.
6. Допустимый угол давления в кулачковом механизме – 32 0
7. Закон движения толкателя на фазах удаления и возвращения - синосоидальный.
ПРИЛОЖЕНИЕ
| Параметр | ВАРИАНТ | |||||||
| РЫЧАЖНЫЙ МЕХАНИЗМ | ||||||||
| Ход поршня Н , м | 0,12 | 0,1 | 0,14 | 0,11 | 0,13 | 0,17 | 0,09 | 0,16 |
| Коэффициент λ = lOA/lAB | 0,22 | 0,19 | 0,2 | 0,25 | 0,2 | 0,23 | 0,25 | 0,21 |
| Диаметр поршня d, м | 0,085 | 0,09 | 0,08 | 0,102 | 0,1 | 0,11 | 0,115 | 0,094 |
| Максимальное давление в цилиндре Рmax , МПа | ||||||||
| Средняя частота вращения кривошипа, мин-1 | ||||||||
| Коэффициент неравномерности движения δ | 1/75 | 1/95 | 1/85 | 1/90 | 1/100 | 1/80 | 1/90 | 1/110 |
| Приведенный к карданному валу момент инерции вращающихся деталей IР , кг·м2 | 0,88 | 0,95 | 0,64 | 0,68 | 0,57 | 0,78 | 0,85 | 0,72 |
| Передаточное отношение от кривошипа к валу генератора u1р | 7,5 | |||||||
| КУЛАЧКОВЫЙ МЕХАНИЗМ | ||||||||
| Полное перемещение плунжера , мм | ||||||||
| Угол рабочего профиля φр , град |
Глава 2. Блок-схема исследования динамики машинного агрегата
Блок-схема исследования динамики машинного агрегата показана на рис. 2.1.
| Динамический синтез машин по коэффициенту неравномерности вращения δ |
| Определение кинематических характеристик исполнительного механизма |
| Определение координат крайних положений рабочего звена и соответствующих им значений обобщённой координаты |
| Определение функций положений, аналогов скоростей и ускорений |
| Определение динамических характеристик машины |
| Динамический анализ машины |
| Определение закона движения звена приведения |
| Динамический анализ исполнительного механизма |
| Кинематический анализ |
| Силовой расчёт |
 |
 ,  |
 ,  |
∆  |
 ,  |
 , ∆  |
 ,  |
 ,  |
 |
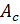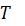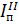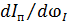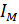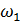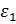Рисунок 2.1
Из схемы видно, что в исследовании можно выделить следующие этапы:
1. Исследование динамики машины:
1.1. Определение кинематических характеристик исполнительного механизма, которое включает нахождение крайних положений рабочего органа и соответствующих ему значений обобщённых координат, вычисление функций положений, аналогов скоростей и ускорений для ряда последовательных положений за цикл движения.
1.2. Определение динамических характеристик звена приведения:
а) приведенных моментов сил полезного сопротивления и движущих сил;
б) приведенного момента инерции ( 
) и его производной.
1.3.Определение закона вращения звена приведения и оценка динамической нагруженности по коэффициенту динамичности.
2. Динамический анализ исполнительного механизма:
2.1. Кинематический анализ, включающий определение скоростей и ускорений точек и звеньев с учётом полученного закона вращения звена приведения.
2.2. Силовой расчёт, целью которого является определение реакций в кинематических парах и уравновешивающего момента.
Глава 3. Динамический синтез и анализ машинного агрегата.
Пункт 3.1. Задачи динамического синтеза и анализа.
Динамический синтез машинного агрегата выполняется по заданному коэффициенту неравномерности δ и заключается в определении постоянной составляющей приведенность сил инерции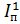 
. Рассчитанная величина 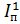конструктивно обеспечивается установкой на валу кривошипа, маховика с моментом инерции 
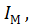который также надо расчитать.
Динамический анализ машинного агрегата заключается в определении закона движения звена приведения, то есть зависимости угловой скорости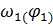 
и углового ускорения 
от обобщенной координаты механизма.
Пункт 3.2. Структурный анализ исполнительного рычажного механизма.
Исполнительный рычажный механизм изображен на рис. 3.1
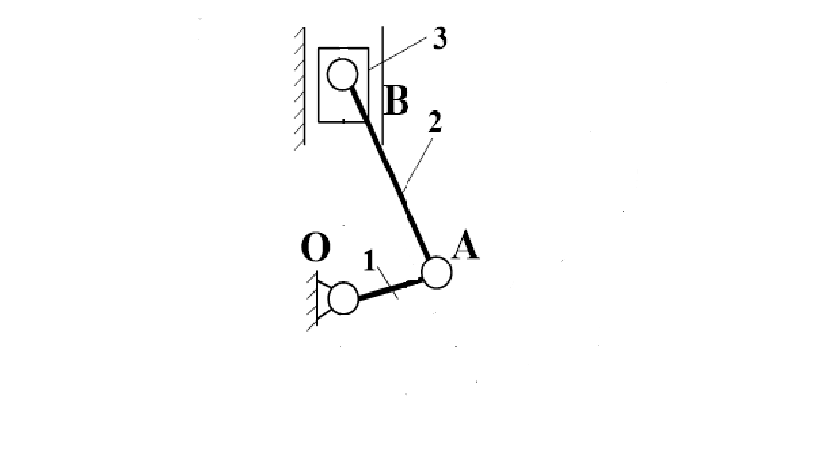Рисунок 3.1
Число подвижных звеньев n = 3.
Число низших кинематических пар 
=4, в том числе вращательные пары – O(1,0), A(1,2), B(2,3), поступательная пара – B(3,0). Число высших кинематических пар 
=0.
Число степеней свободы механизма
W=3n-2 - =3·3-2·4-0=1
Начальным звеном является кривошип 1. Механизм образован из механизма 1-го класса (0,1) и структурной группы (2,3) (рисунок 3.2).
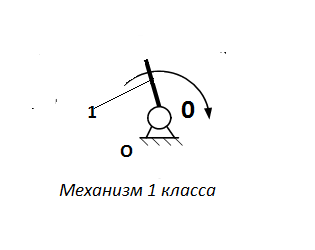
Рисунок 3.2
Формула строения механизма: I (1,0) → II (2,3), механизма 2-го класса.
Пункт 3.3 Определение основных размеров, масс и моментов инерции звеньев.
Схема для определения основных размеров на рис. 3.3.
 |
| A |
 |
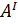| O |
 |
 |
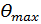| B |
 |
 |
 | |||
 | |||
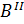Рисунок 3.3
Входные параметры:
а)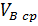 
(м/с)- средняя скорость движения ползуна;
б)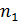 
(об/мин) - частота вращения кривошипа 1;
в) e=0 – эксцентриситет;
г)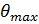 
- максимальный угол давления;
H=0,16м – ход поршня
Так, как e=0, то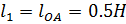 
= 0.5·0.16=0.08м
Из прямоугольного треугольника OAB:
= 
= 
= 
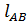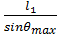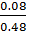=0.16м
Из рис 3.1 и рис.3.3 видно, что механизм центральный, поэтому смещение e оси ползунов равно 0. Средняя угловая скорость кривошипа 1:
= 
= 
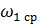= 209.33 рад/с.
Массы звеньев:
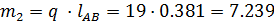кг – масса шатуна;
Где q = 19 кг/м.
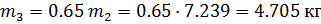– масса поршня;
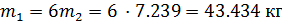– масса кривошипа;
Основные центральные моменты инерции звеньев:
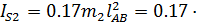7.239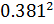 
= 0.179 кг· 
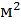- момент инерции шатуна;
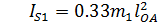= 0.33 ·43.434· 
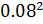= 0.0917 кг· 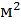– момент инерции кривошипа;
Определим центр масс звеньев:
= 0;
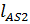= 0.35 
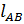= 0.35·0.381 = 0.133м
Определим приведенный момент инерции всех вращающихся звеньев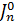 
:
= 
= 
= 
= 
= 
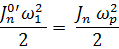
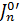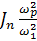= 0.0072кг
= 
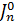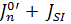= 0.0072+0.0917 = 0.0989кг·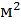
Пункт 3.4 Построение 12 планов положения механизма.
Для построения планов выбираем масштабный коэффициент длин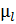 
= 0.001 
.
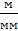Определяем чертежные размеры звеньев механизма:
= 
= 
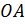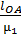= 80мм;
= 
= 
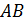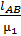= 381мм;
= 
= 
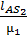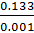= 133мм;
Методом засечек строим 12 последовательных планов положений механизма через 30 градусов по углу поворота кривошипа OA, начиная с крайнего положения 1, в котором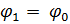 
и звенья OA и AB вытягиваться в одну прямую линию. Второе крайнее положение 
, в котором звенья OA и AB накладываться одно на другое, находим дополнительно. Все положения нумеруются в направлении вращения кривошипа.
На шатуне 2, отрезком 
отмечаем положение точки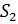 
на всех планах и соединяем их плавной линией, получая траекторию движения центра масс шатуна.
Пункт 3.5 Кинематический анализ механизма.
Начальная обобщенная координата механизма соответствующая верхней мертвой точке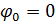 
.
Обобщенная координата для контрольного положения 
:
- номер положения;
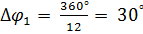– шаг по обобщенной координате;
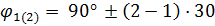– для положения 2;
Подпункт 3.5.1 Графический метод кинематического анализа.
Выполняем расчет аналогов скоростей для контрольного положения 2.
Аналог скоростей точки A равен:
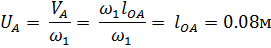
Принимаем масштабный коэффициент аналогов скоростей 
. Тогда отрезок, изображающий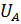 
, равен:
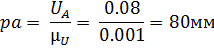
Аналог скорости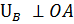 
и направлен в сторону вращения кривошипа 1.
Для построения плана аналогов скоростей используются следующие векторные уравнения (на основании теоремы о сложении скоростей в плоском движении):
где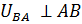 
, 
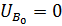(точка 
направляющих ползуна неподвижна), 
.
Точку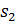 
на плане аналогов скоростей находим по теореме подобия:
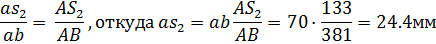
Находим на плане проекции точки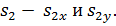 
Из плана находим передаточные функции (аналогов скоростей):
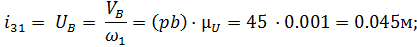
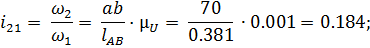
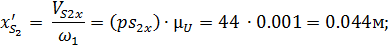
Сопоставление результатов расчетов приведено в таблице 3.1
Подпункт 3.5.2 Аналитический метод расчета.
Расчет выполняем методом замкнутого векторного контура. Расчетная схема представлена на рис 3.4.
| O |
 |
 |
 |
 |
 |
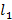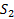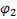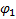| Y |
| A |
| B |
 |
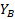| X |
 |
 |
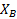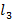Рисунок 3.4
.
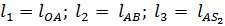Основное уравнение замкнутого векторного контура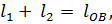 
уравнение проецируется на координатной оси, и уравнение проекции дифференцируется по обобщенной координате 
. После первого дифференцирования получим уравнение выражения для аналогов скоростей, а при повторном дифференцировании - получим уравнение для аналогов ускорения.
Для вертикальных механизмов расчет вычислений имеет вид:
1. 
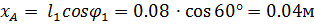
2. 
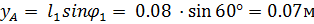
3. 
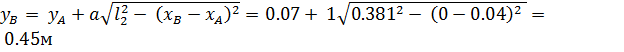
4. 
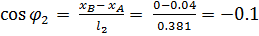
5. 
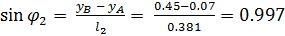
6. 
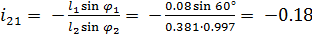
7. 
8. 
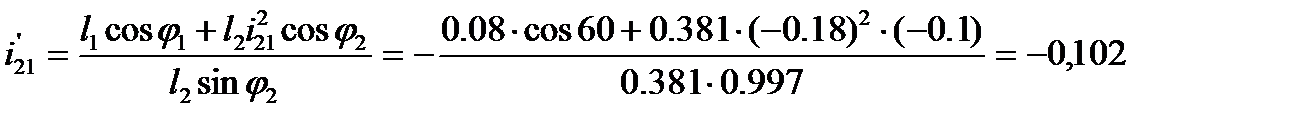
9. 
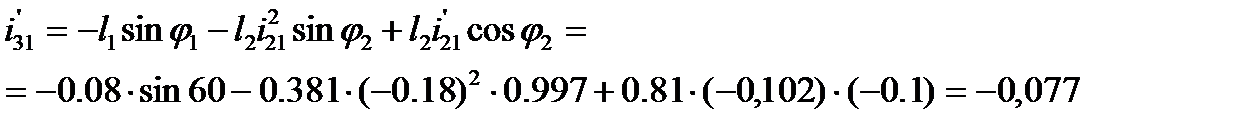
10. 
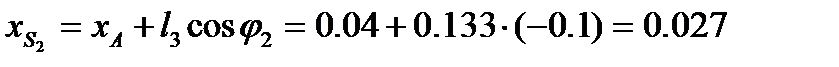
11. 
12. 
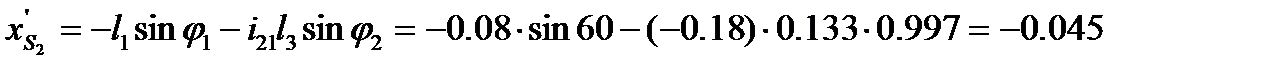
13. 
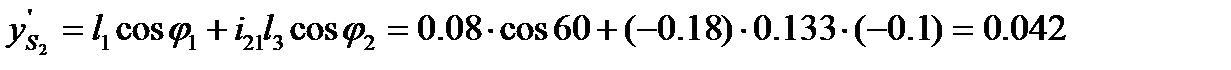
14. 
15. 
16. 
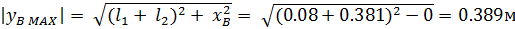
17 . 
Таблица 3.1
| Параметры | Единицы измерения | Аналитический метод | Графический метод |
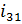 | м | 0.047 | 0.045 |
 | - | -0.18 | 0.184 |
 | м | -0.045 | 0.044 |
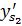 | м | 0.042 | 0.045 |
Пункт 3.6 Определение сил движущих действующих на поршень.
На листе 1 изображаем индикаторную диаграмму давлений в цилиндре. Для этого задаемся максимальной ординатой давления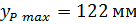 
. Тогда:
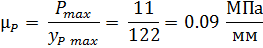
Значение ординат давлений в каждом положении записываем в таблицу 3.2:
Таблица 3.2
| № | |||||||||||||
 | |||||||||||||
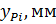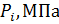 | 8,82 | 4,95 | 2,25 | 0,99 | 0,72 | 0,72 | 0,54 | 0,18 | 0,36 | 2,07 | 4,95 | 8,82 | |
 |
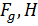где 
- диаметр поршня;
Формула, по которой рассчитываем давление в поршне:
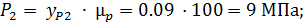
Определяем силу, действующую в поршнях:
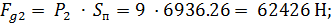
Пункт 3.7 Динамическая модель машинного агрегата.
В движении входного звена исполнительного рычажного механизма имеют место колебания угловой скорости, основными причинами которых являются:
1) несовпадение законов изменения сил сопротивления и движущих сил в каждый момент времени;
2) непостоянство приведенного момента инерции звеньев исполнительного и некоторых вспомогательных магазинов.
Чтобы учесть влияние названных причин на закон движения входного звена исполнительного механизма, составляться упрощенная модель машинного агрегата и на основе – математическая модель, устанавливающая функциональную взаимосвязь исследуемых параметров.
Наиболее простой динамической моделью машинного агрегата может быть одномассавая модель, представленная на рис. 3.5.
P AAAAZHJzL2Rvd25yZXYueG1sTI/BTsMwEETvSPyDtUjcqN2URG0ap6IIJG4ogQ9w4iWJaq+j2G0C X497guNoRjNvisNiDbvg5AdHEtYrAQypdXqgTsLnx+vDFpgPirQyjlDCN3o4lLc3hcq1m6nCSx06 FkvI50pCH8KYc+7bHq3yKzciRe/LTVaFKKeO60nNsdwangiRcasGigu9GvG5x/ZUn62E+X1XVUqY t5/1UjcvCT86So9S3t8tT3tgAZfwF4YrfkSHMjI17kzaMxN1ksUvQUKyS1Ng18TmMQPWSNiIbAu8 LPj/D+UvAAAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAA AABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAA AAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAFV3hP7/AQAAowMAAA4AAAAAAAAA AAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAKQPGYXfAAAACwEAAA8AAAAA AAAAAAAAAAAAWQQAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAABlBQAAAAA= " strokecolor="windowText"/>
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
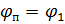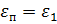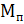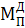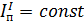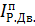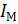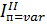Рисунок 3.5
В качестве такой модели рассматривается условное вращающееся звено – звено приведения, которое имеет момент инерции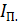 
относительно оси вращения (приведенный момент инерции) и находиться под действием сил 
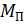(приведенного момента сил). В свою очередь 
, где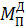 
– приведенный момент движущих сил; 
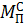– приведенный момент сил сопротивления. Кроме того, 
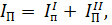где – постоянная составляющая приведенного момента инерции;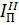 
– переменная составляющая приведенного момента инерции. В величину 
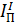входят собственный момент инерции кривошипа ( 
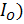, приведенные моменты инерции ротора электродвигателя и передаточного механизма ( 
, 
а также момента инерции 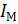добавочной массы (маховика), причем необходимость установки маховика определяется на основании заданной степени неравномерности движения звена приведения.
Динамические характеристик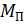и и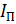 
должны быть такими, чтобы закон вращения звена приведения был таким же, как и у главного вала машины (кривошипа 1 основного исполнительного рычажного механизма), т.е. 
Пункт 3.8 Определение приведенных моментов сил движущих и сил сопротивления.
Приведенный момент сил 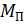представляется в виде алгебраической суммы
Определение 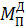выполняется из условия равенства мгновенных мощностей
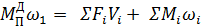
Откуда
где 
– проекции силы 
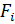на оси координат;
- проекции аналога скорости точки приложения силы;
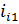– передаточная функция от i-го звена, к которому приложен момент 
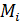, к звену 1;
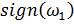= +1 при направлении вращения звена 1 против часовой стрелки;
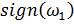= - 1 при направлении вращения звена 1 по часовой стрелке.
В формуле 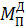силы 
, 
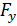и моменты 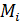берутся со знаками, соответствующими правой системе координат (положительное направление вращения – против часовой стрелки).
Так, для вертикального механизма (рис. 3.5) 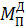определяется из равенства 
Откуда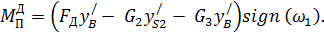 
 |
 |
 |
 |
| |
 |
| |
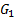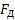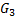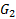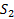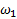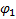| Y |
| X |
| A |
| B |
O,  |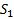
Рисунок 3.6.